Heights and Distances

In the previous chapter, we have studied about trigonometric ratios. In this chapter, we will be looking at some ways in which trigonometry is used in the life around you.

Looking at a tower

Say we are looking at the top of a tower. From our eye level a line can be drawn to the top of the tower which is called the line of sight. This line of sight makes an angle with the horizontal, which is called the angle of elevation of the top of the tower from the eye of the observer i.e. when we raise our head to look at the object.

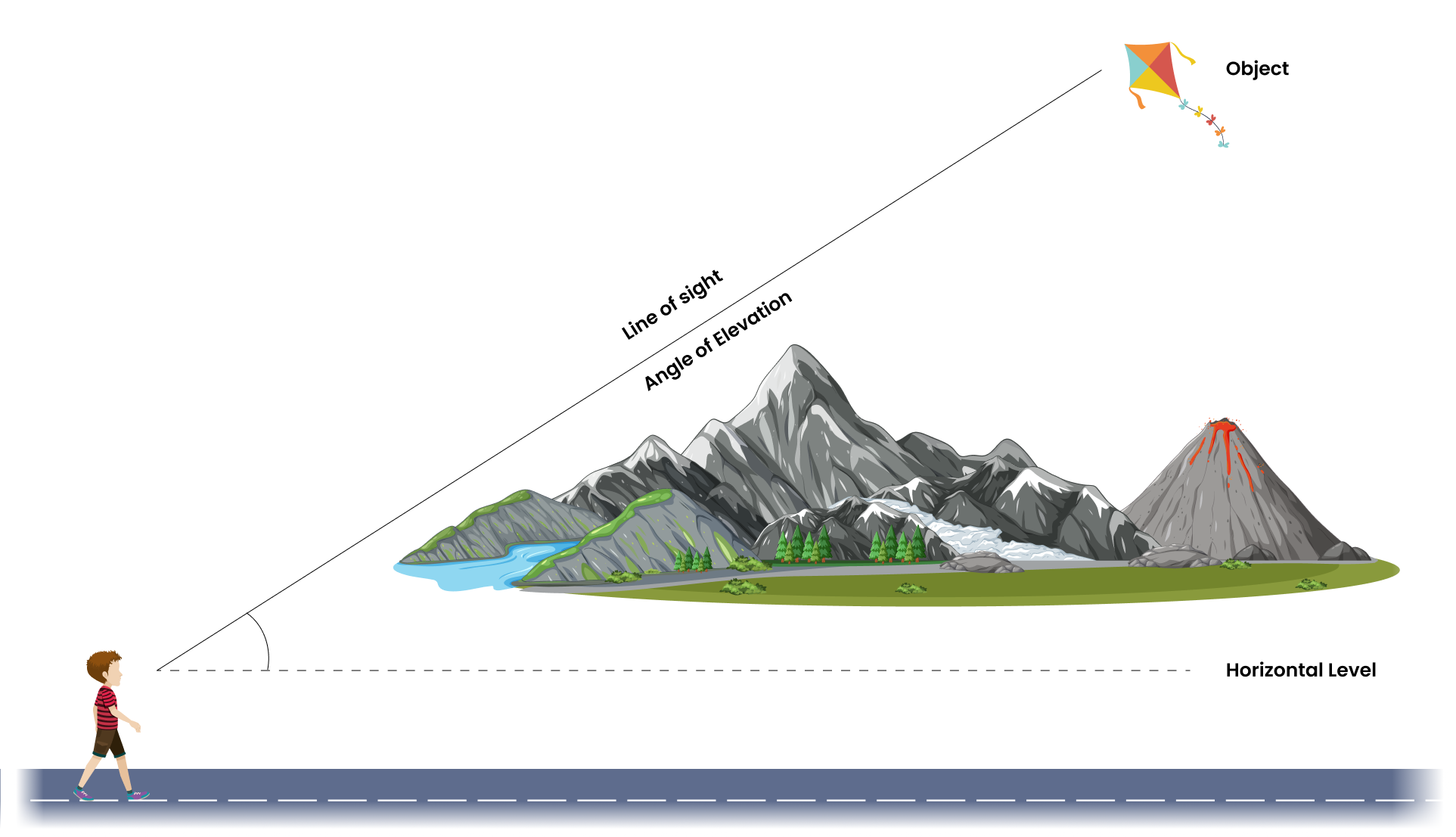
Now, look at the reverse case. Say, somebody is looking at us from the top of the tower In this case, the line of

sight (drawn from the eye of the observer) is below the reference horizontalvertical line.

The angle so formed by the line of sight with the horizontal is called the angle of depression.

Thus, the angle of depression of a point on the object being viewed is the angle formed by the line of sight with the horizontal when the point is below the horizontal level, i.e., the case when the observer lowers their head to look at the point being viewed.

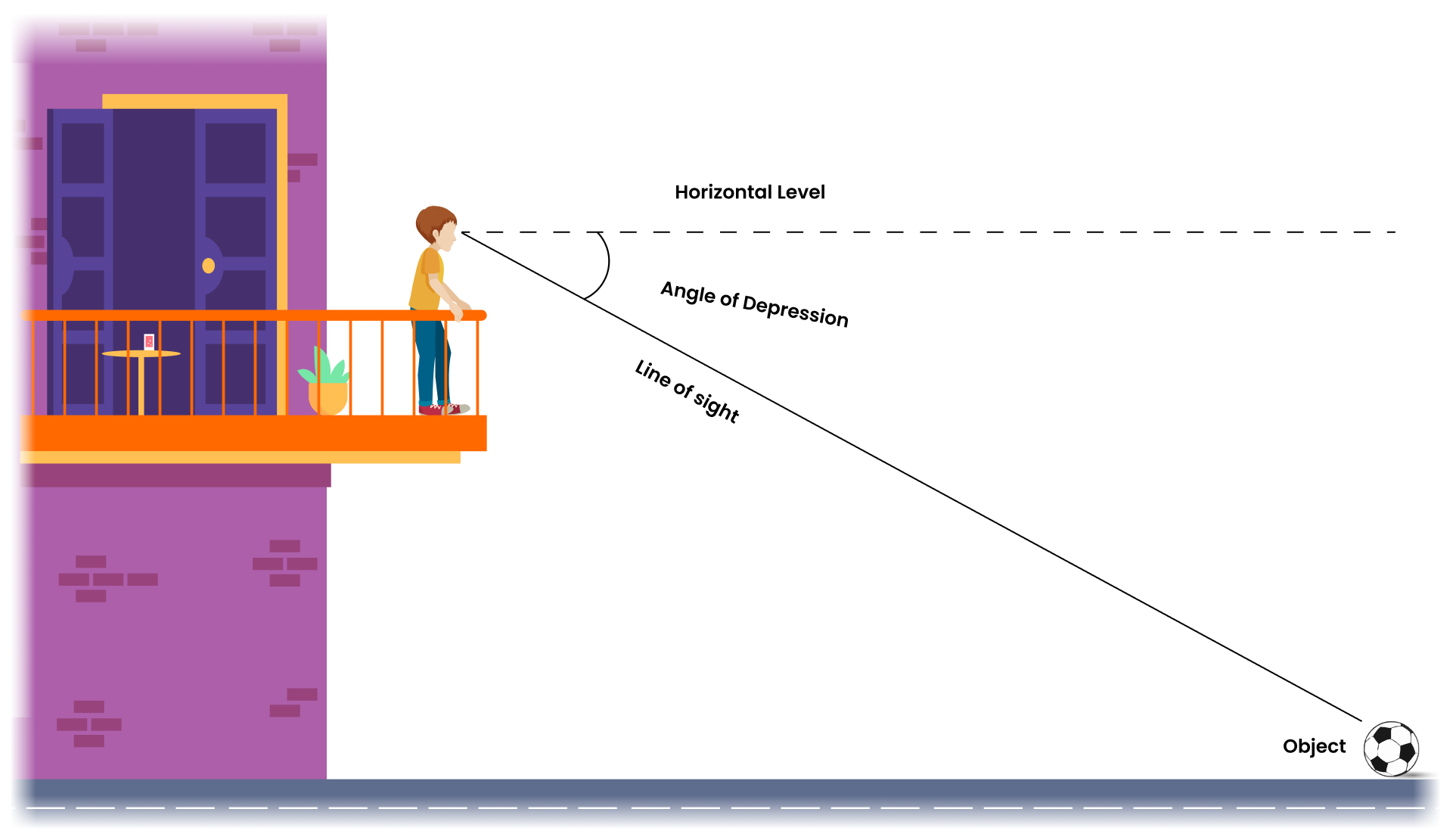
Now, let's look at the figure given below.

A person is looking at the top of the hill from the ground level and another person is watching the ground from the top of the hill.

Can you identify the lines of sight, and the angles so formed in the figure?

What are the angles of elevation (or) angles of depression?

Angle of elevation : ∠CAB∠ABC Angle of depression : ∠ABH∠CAB Line of Sight : ABBC

We need the height of observer because we need to add that as the triangle is formed only till the horizontal level.

Assuming that the above three conditions are known, can we determine the height of the mountain? YesNo

Given that we know the distance AC and the angle: the trigonometric ratio that can be used to find the height is tan(angle of elevation)sin(angle of elevation)cos(angle of elevation).

So, the height of the mountain is :

tanangle of elevation x Distance of A from the mountain + height of A

1. A tower stands vertically on the ground. From a point on the ground, which is 15 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower.

Instructions

Solution: First let us draw a simple diagram to represent the problem. Here AB represents the tower, CB is the distance of the point from the tower and ∠ACB is the angle of elevation.

We need to determine the height of the tower, i.e., AB. Also, ACB is a triangle, right-angledacute-angled at B.

To solve the problem, we choose the trigonometric ratio tan (or cot), as the ratio involves ABAD and BCAC.

Now, tan 60° = ABBCBCAB

Putting values,

33 = AB15AC15

AB = 15315

Hence, the height of the tower is 153 m.

2. An electrician has to repair an electric fault on a pole of height 5 m. She needs to reach a point 1.3 m below the top of the pole to undertake the repair work. What should be the length of the ladder that she should use which, when inclined at an angle of 60° to the horizontal, would enable her to reach the required position? Also, how far from the foot of the pole should she place the foot of the ladder? (take 3 = 1.73)

Instructions

Solution: The electrician is required to reach the point B on the pole AD.

So, BD = –

= 5 – 1.3 = m.

Here, BC represents the ladder. We need to find its length of the of the right triangle BDC.

Now, which trigonometic ratio should we consider?

It should be sin 60°cos 60°.

So, BDBCBCBD = sin 60°

/BC = 3213

Therefore, BC = 3.7×23 = m (upto two decimal places)

Thus, the length of the ladder should be 4.28 m

Now, DCBD = cot 60°tan 60° = 133

DC = 3.73 = m (upto two decimal places)

Therefore, she should place the foot of the ladder at a distance of 2.14 m from the pole.

3. An observer 1.5 m tall is 28.5 m away from a chimney. The angle of elevation of the top of the chimney from her eyes is 45°. What is the height of the chimney?

Instructions

Solution : Here, AB is the chimney, CD the observer and ∠ ADE the angle of elevation. In this case, ADE is a triangle, -angled at E and we are required to find the height of the chimney.

We have AB = + BE = + and DE = CB = m

To determine AE, we choose a trigonometric ratio, which involves both AE and DE.

So, tan 45°sin 45° = AEDE

= AE28.5

Therefore, AE = m

So the height of the chimney (AB) = AE + BE = + m = m.

Thus, height of the chimney is 30 m.

4. From a point P on the ground the angle of elevation of the top of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flagstaff from P is 45°. Find the length of the flagstaff and the distance of the building from the point P. (You may take 3 = 1.732)

Instructions

Solution : AB denotes the height of the building, BD the flagstaff and P the given point. Note that there are two right triangles PAB and PAD. We are required to find the length of the flagstaff, i.e. DB and the distance of the building from the point P, i.e. PA.

Since, we know the height of the building AB, we will first consider the right triangle PAB.

We have tan 30°cot 30° = ABAP

133 = /AP

Therefore, AP = 103310

i.e. the distance of the building from P is 103 m = m. (upto two decimal places)

Next, let us suppose DB = x m. Then AD = 10+x10x m.

Now, in right triangle PAD, tan 45° = ADAPAPAD = 10+x10310310+x

Therefore, = 10+x103

i.e., x = 103−1103+1 = (upto two decimal places)

So, the length of the flagstaff is 7.32 m.

5. The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun’s altitude is 30° than when it is 60°. Find the height of the tower.

Instructions

Solution : AB is the tower and BC is the length of the shadow when the Sun’s altitude is 60°, i.e., the angle of elevation of the top of the tower from the tip of the shadow is 60° and DB is the length of the shadow, when the angle of elevation is °.

Now, let AB be h m and BC be x m. According to the question, DB is m longer than BC.

So, DB = (40 + x) m

Now, we have two right triangles ABC and ABDBCD.

In triangle ABC, tan 60° = ABBCBCAB

313 = hxxh (1)

In triangle ABD, tan 30° = ABBDBDAB

133 = hx+40x+40h (2)

From (1), we have h = x33x

Putting this value in (2), we get x33 = x + 40, i.e. = x + 40

Thus, x =

So, h = 203203 [From (1)]

Therefore, the height of the tower is 203 m.

6. The angles of depression of the top and the bottom of an 8 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multistoreyed building and the distance between the two buildings.

Instructions

Solution : PC denotes the multistoryed building and AB denotes the 8 m tall building. We are interested to determine the height of the multi-storeyed building, i.e. PC and the distance between the two buildings i.e. .

Look at the figure carefully. Observe that PB is a to the parallel lines PQ and BD.

Therefore, ∠ QPB and ∠ PBD are alternate interioralternate exterior angles and thus are .

So ∠ PBD = °. Similarly, ∠ PAC = °.

In right triangle PBD, we have:

PDBDBDPD = tan 30° = 133

BD = 313PD

In right triangle PAC, we have:

PCACACPC = tan 45° =

PC =

Also, PC = PD +

Therefore, PD + DC =

Since, AC = BD and DC = AB = m, we get:

PD + 8 = BD = 3

This gives PD = 83−1 = 83+13−13+1 = 43+143−1

So, the height of the multi-storeyed building is 43+1+8 = 43+343−3 and the distance between the two buildings is also 43+343−3 m.

Example 7

7. From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°, respectively. If the bridge is at a height of 3 m from the banks, find the width of the river.

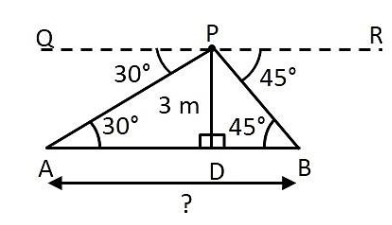
Solution : A and B represent points on the bank on opposite sides of the river, so that AB is the width of the river. P is a point on the bridge at a height of 3 m, i.e. DP = m.

We are interested to determine the width of the river, which is the length of the side ABAP of the triangle APB.

Now, AB = AD +

In right triangle APD, ∠ A = °.

So, tan 30°sin 30° = PDADADPD

13 = 3ADAD3

AD = 3333 m

Also in right triangle PBD, ∠ B = °. So, BD = PD = m.

Now, AB = BD + AD = 3+33 = 31+333 m.

Therefore, the width of the river is 31+3 m.

Text based adventure game