Extra Curriculum Support

SecA

1. Which of the following points lie on the y-axis: A(0,0), B (3,0), C(0,3), D(0,0), E(-5,0), F(0,-1), G(9,0), H(0,-8)

2. The point (0,-4) lies:

(a) On the negative direction of y-axis

(b) in quadrant III

(c) in quadrant IV

(d) On the negative direction of X-axis

3. P(5,-7) is a point on a graph. Draw PM ⊥ y-axis. The coordinates of M are:

(a) On the negative direction of y-axis

(b) in quadrant III

(c) in quadrant IV

(d) On the negative direction of x-axis

Sol

1. Solution:

So, the points that lie on the y-axis are:

A(0, 0)

C(0, 3)

D(0, 0)

F(0, -1)

H(0, -8)

2. Solution: Option (a)

3. Solution: Option (a)

SecB

4. Seema has a 10 x 10 kitchen garden attached to her kitchen. She divides it into a 10 x 10 grid and wants to grow some vegetables and herbs in the kitchen. She puts some soil and manure and sows a green chili plant at A, a coriander plant at B and a tomato plant at C. Her friend Khusum visited the garden and praised the plants grown there. She points out that they seem to be in a straight line. Using distance formula or some other method, check if her statement is true.

Sol

Solution: To check if the points (2,2), (5,4.5), and (7,6.5) are collinear, we can use the concept of slopes. If the slopes of the line segments between any two pairs of these points are equal, then the points are collinear.

The slope m of a line passing through points x1,y1 and x2,y2:

m = y2−y1x2−x1

Calculate the slope between the points (2,2) and (5,4.5)

m1 = 4.5−25−2 = 2.53 = 56

Calculate the slope between the points (5,4.5) and (7,6.5)

m2 = 6.5−4.57−5 = 22 = 1

Calculate the slope between the points (2,2) and (7,6.5)

m3 = 6.5−27−2 = 4.55 = 910

Since the slopes are not equal, the points are not collinear.

The points (2,2), (5,4.5), and (7,6.5) are not collinear.

SecC

5. Write the equation represented by AB and PQ. Also find the co-ordinates of the their intersection point.

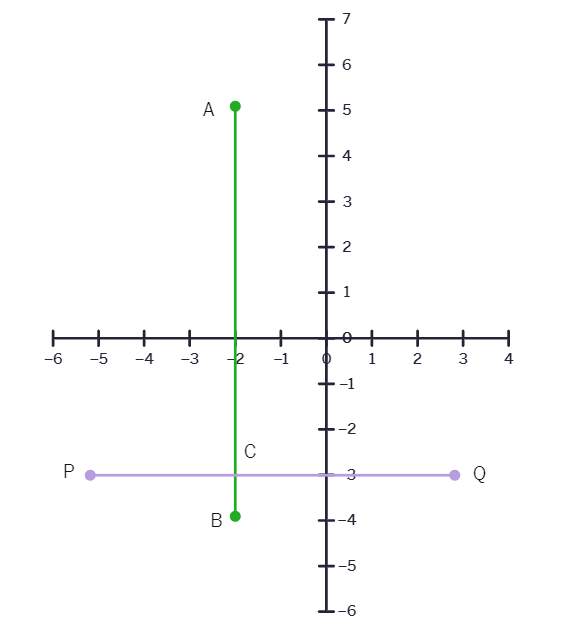
Sol

Solution: Equation AB

Since the x-coordinate for both points is −2, the equation of the line is: x = −2

The equation of the line passing through the points (−2,0) and (−2,−3) is: x = −2 ​ Equation PQ

Since both points have the same y-coordinate (−3), this is a horizontal line.

Since the y-coordinate for both points is −3, the equation of the line is: y = −3

The equation of the line passing through the points (−2,−3) and (0,−3) is: y = −3

Intersection Point of AB and PQ

The intersection point is where both equations are satisfied simultaneously. This means finding the common x and y values that satisfy both equations.

From the equations: x = −2 and y = −3

The intersection point of the lines y = −3 and x = −2 is: (−2,−3)

Problem 1

1. A farmer discovered an ancient well on his property, marked at coordinates (4, 5). To ensure safety, he decided to build a fence around the well. If the fence needs to be circular and must cover an area of 100 square units, find the equation of the circle that represents the fence. Determine the coordinates of any point on the fence that touches the ground.

Sol

Solution: To determine the equation of the circle representing the fence around the well, we need to use the given information:

The center of the circle is at the coordinates (4,5).

The area of the circle is 100 square units.

The area of a circle is given by:

Area = πr2

Given that the area is 100 square units, we can solve for the radius r: 100 = πr2

r = 100π = 10π

Now, we can write the equation of the circle in standard form: x−h2+y−k2=r2

Substituting h = 4, k = 5, and r2 = 110π : x−42+y−52=100π

Next, let's determine the coordinates of any point on the fence (circle) that touches the ground. The ground typically refers to the x-axis (where y=0).

To find where the circle intersects the x-axis, set y = 0 in the equation of the circle:

x−42+0−52=100π

x−42=100π−25

x = 4±100π−25

So, the coordinates of the points where the circle intersects the x-axis (the ground) are:

(4+100π−25, 0) and (4−100π−25, 0)

Therefore, the equation of the circle is: x−42+y−52=100π and the coordinates of the points where the fence touches the ground are: (4+100π−25, 0) , (4−100π−25, 0)

Problem 2

2. During a trekking expedition, a group of students found a steep cliff represented by the line y = 8 on a coordinate grid. They observed a bridge spanning the cliff, starting at (2, 5) and ending at (8, 5). Calculate the length of the bridge and determine the coordinates of its midpoint.

Sol

Solution:

Length of the Bridge

The coordinates of the starting point of the bridge are (2,5) and the ending point are (8,5). Since both points share the same y-coordinate, the bridge is a horizontal line segment.

The length of a horizontal line segment can be calculated as the difference between the x-coordinates of the two points: Length = ±x2−x1

Substituting the given coordinates: Length = ∣8−2∣

Length=6

So, the length of the bridge is 6 units.

Midpoint of the Bridge

The midpoint (M) of a line segment with endpoints x1,y1 and x2,y2 is calculated as:

M = x1+x22,y1+y22

Substituting the given coordinates:

M = 2+82,5+52 = (5,5)

So, the coordinates of the midpoint of the bridge are (5,5).

Problem 3

3. During a cleanliness drive in their locality, students marked four corners of a square garden on a coordinate grid. The coordinates of three corners are (2,3), (6,3), and (6,7). They realized that the fourth corner, (x, y), needs to be determined. If the garden's area represents unity and it must be square-shaped, find the coordinates (x, y) of the fourth corner.

Sol

Solution:

We have the points:

A(2,3)

B(6,3)

C(6,7)

The points B(6,3) and C(6,7) have the same x-coordinate, so they form a vertical side of the square. The length of this side can be calculated as the difference in their y-coordinates:

Length = ∣7−3∣ = 4

Similarly, the points A(2,3) and B(6,3) have the same y-coordinate, so they form a horizontal side of the square. The length of this side can be calculated as the difference in their x-coordinates:

Length = ∣6−2∣ = 4

Since both lengths are 4, we can confirm that the side length of the square is 4 units.

Given that A(2,3), B(6,3) and C(6,7) are consecutive corners of the square, the fourth corner must complete the square. Since the square's side length is 4, we can determine the coordinates by moving vertically or horizontally by 4 units from the known corners.

The known points suggest the following positions for the fourth corner: Moving vertically from A(2,3): Since A(2,3) is directly below C(6,7), moving vertically by 4 units gives the fourth corner's coordinates as: D = (2,7).

To verify, the points should form a square: A(2,3), B(6,3), C(6,7), D(2,7).

Check distances: AB = ∣6−2∣ = 4

BC = ∣7−3∣ = 4

CD = ∣6−2∣ = 4

DA = ∣7−3∣ = 4

All sides are equal, confirming a square shape.

The coordinates of the fourth corner D are (2,7).

Q1

1. The vertices of triangle △ABC are A(1, 3), B(4, 6), and C(7, 3). Determine the equation of the perpendicular bisector of side AC. Explain how you can use this perpendicular bisector to verify that △ABC is isosceles.

Sol

Solution: To determine the equation of the perpendicular bisector of side AC in triangle ΔABC with vertices A(1,3), B(4,6), and C(7,3), and to verify if ΔABC is isosceles using the perpendicular bisector, follow these steps:

The midpoint (M) of a line segment with endpoints x1,y1 and x2,y2 is calculated as:

M = x1+x22,y1+y22

For points A(1,3) and C(7,3):

Substituting the given coordinates:

M = 1+72,3+32 = (4,3)

The slope m of a line passing through points x1,y1 and x2,y2:

m = y2−y1x2−x1

For A(1,3) and C(7,3):

m = 3−37−1 = 0

The slope of AC is 0, meaning AC is a horizontal line.

The slope of the perpendicular bisector is the negative reciprocal of the slope of AC. Since the slope of AC is 0, the perpendicular slope is undefined (a vertical line).

Since the perpendicular bisector is a vertical line passing through the midpoint (4,3), the equation is: x = 4

For ΔABC to be isosceles, two sides must be equal in length. We will check if the perpendicular bisector passes through vertex B(4,6).

The perpendicular bisector's equation is x = 4, and vertex B's x-coordinate is 4, indicating that B lies on the perpendicular bisector.

Since the perpendicular bisector of side AC passes through vertex B, it confirms that ΔABC is isosceles with AB = BC.

The equation of the perpendicular bisector of side AC is : x = 4 ​ This perpendicular bisector passing through vertex B(4,6) verifies that ΔABC is isosceles.

Q2

2. A circle with center O and radius 5 units passes through the points (3, 4) and (7, 4). Determine the coordinates of the center O of the circle and write the equation of the circle in standard form. Justify your steps.

Sol

Solution: To determine the coordinates of the center O of a circle with radius 5 units that passes through the points (3,4) and (7,4), and to write the equation of the circle in standard form, follow these steps:

Since the points (3,4) and (7,4) lie on the circle and are collinear (they share the same y-coordinate), they form a horizontal chord. The midpoint M of this chord can be found as follows:

M = x1+x22,y1+y22

For (3,4) and (7,4):

M = 3+72,4+42 = 5,4

The center O of the circle is on the line perpendicular to the chord at its midpoint M. Since the chord is horizontal, the perpendicular line will be vertical. Therefore, the x-coordinate of O is the same as the midpoint M, which is 5.

The distance from the center O to any point on the circle (like (3,4) or (7,4)) is the radius of the circle, which is 5 units. Let the coordinates of the center O be (5,y). The distance between the center and a point on the circle can be given by:

x−x12+y−y12 = r

For point (3,4):

5−32+y−42 = 5

4+y−42=25

y−42=21

y = 4±21

Now we have two possible centers: O1=5,4+21 (or) O2=5,4−21

Using the standard form of the circle's equation x−h2+y−k2=r2:

For O1=5,4+21

x−52+y−4+212=25

For O2=5,4−21

x−52+y−4−212=25

Justification

The midpoint method ensures the center lies on the perpendicular bisector of the chord, thus equidistant from both endpoints. The distance calculation confirms the points lie on the circle with the correct radius.

The coordinates of the center O of the circle are either: 5,4+21 (or) 5,4−21

The equation of the circle in standard form is: x−52+y−4−212=25

Q3

3. A rectangular garden has one vertex at (2, 3) and diagonally opposite vertex at (8, 7). Determine the coordinates of the other two vertices of the rectangle. Discuss how you can use midpoint formulas and distance formulas to verify your solution.

Sol

Solution: To determine the coordinates of the other two vertices of a rectangle with one vertex at (2,3) and the diagonally opposite vertex at (8,7), and to verify the solution using midpoint and distance formulas, follow these steps:

Let A(2,3) and C(8,7) be the given diagonally opposite vertices of the rectangle.

The midpoint M of line segment joining x1,y1 and x2,y2 can be found as follows:

M = x1+x22,y1+y22

For points A(2,3) and C(8,7):

M = 2+82,3+72 = 5,5

This implies: x1+x2=10 and y1+y2=10

Also, the side lengths of the rectangle must be consistent with the diagonal lengths. Specifically, the distances between A and B, B and C, C and D, and D and A must satisfy the properties of a rectangle. Let’s use the fact that A and C have a consistent relationship with B and D:

Assuming B and D are vertically aligned with A and C.

Since A(2,3) and C(8,7) form a rectangle with equal side lengths horizontally and vertically:

The horizontal distance (width) is ∣8−2∣ = 6

The vertical distance (height) is ∣7−3∣ = 4

Using this: B should be (2+6,3) = (8,3)

D should be (2,3+4) = (2,7)

Therefore, the coordinates of the other two vertices are: B(8,3), D(2,7).

Midpoint Verification:

Midpoint of AC: (5,5)

Midpoint of BD: (5,5)

Distance Verification:

Distance AB: 8−22+3−32 = 62+0 = 6

Distance BC: 8−82+7−32 = 0+42 = 4

Distance CD: 8−22+7−72 = 62+0 = 6

Distance AD: 2−22+7−32 = 0+42 = 4

All side lengths are consistent with the properties of a rectangle, verifying our solution.

The coordinates of the other two vertices of the rectangle are: (8,3) and (2,7)

Questions

1. Abscissa of all the points on the x-axis is:

(A) 0

(B) 1

(C) 2

(D) any number

2. The points whose abscissa and ordinate have different signs will lie in:

(A) I and II quadrants

(B) II and III quadrants

(C) I and III quadrants

(D) II and IV quadrants

Sol

Solution: Option (d)

Solution: Option (d)

Questions

3. Without plotting the points indicate the quadrant in which they will lie, if:

(i) ordinate is 5 and abscissa is – 3

(ii) abscissa is – 5 and ordinate is – 3

(iii) abscissa is – 5 and ordinate is 3

(iv) ordinate is 5 and abscissa is 3

4. Plot the following points and write the name of the figure obtained by joining them in order: P(– 3, 2), Q (– 7, – 3), R (6, – 3), S (2, 2)

5. In the figure, LM is a line parallel to the y-axis at a distance of 3 units.

(i) What are the coordinates of the points P, R and Q?

(ii) What is the difference between the abscissa of the points L and M?

6. Write the coordinates of the vertices of a rectangle whose length and breadth are 5 and 3 units respectively, one vertex at the origin, the longer side lies on the x-axis and one of the vertices lies in the third quadrant.

7. Three vertices of a rectangle are (3, 2), (– 4, 2) and (– 4, 5). Find the coordinates of the fourth vertex.

8. Plot the points A (1, – 1) and B (4, 5). (i) Draw a line segment joining these points. Write the coordinates of a point on this line segment between the points A and B. (ii) Extend this line segment and write the coordinates of a point on this line which lies outside the line segment AB.

Sol

3. Solution: (i) II Quadrant (ii) III Quadrant (iii) II Quadrant (iv) I Quadrant

4. Solution: To determine the nature of the figure, we need to check the lengths of the sides and the angles between them.

Calculate the lengths of the sides PQ: Distance between P(−3,2) and Q(−7,−3)

PQ = −7−−32+−3−22 = −42+−52 = 16+25 = 41

QR: Distance between Q(−7,−3) and R(6,−3)

QR = −7−62+−3−−32 = −132+02 = 169+0 = 13

RS: Distance between R(6,−3) and S(2,2)

RS = 2−62+2−−32 = −42+52 = 16+25 = 41

SP: Distance between S(2,2) and P(−3,2)

SP = −3−22+2−22 = 5+0 = 5

Thus,

PQ = 41 , QR = 13 , RS = 41, SP = 5

The opposite sides PQ and RS are equal (41). The adjacent sides QR and SP are not equal, nor are the angles between them 90 degrees, so the figure is not a rectangle or a square. Given the lengths and the lack of 90-degree angles, the figure is most likely an irregular quadrilateral.

The figure obtained by joining the points P(−3,2), Q(−7,−3), R(6,−3), and S(2,2) in order is an irregular quadrilateral.

5. Solution: (i) From the figure, we see:

P = (3,2) , Q = (3,-1) and R = (3,0)

Coordinates of the points are: (3,2) , (3,-1) and (3,0).

(ii) Difference between the abscissa of the points L and M = 3 - 3 = 0.

The difference between the abscissa of the points L and M is 0.

6. Solution: Let A be at the origin: A(0,0).

Since the longer side (length) lies on the x-axis, place another vertex along the x-axis 5 units to the right of A.

The vertex to the right of A is B(5,0). Since the breadth is 3 units, move vertically downwards from both A and B by 3 units to get the other two vertices.

Moving vertically downward from A by 3 units: C(0,−3)

Moving vertically downward from B by 3 units: D(5,−3)

The coordinates of the vertices of the rectangle are: A(0,0)B(5,0) C(0,−3) D(5,−3)

7. Solution: Let the vertices be: A(3,2) , B(−4,2) , C(−4,5).

The fourth vertex D should form the opposite corner of the rectangle with vertex C and should be aligned with vertices A and B.

A(3,2) and B(−4,2) lie on the same horizontal line (same y-coordinate). B(−4,2) and C(−4,5) lie on the same vertical line (same x-coordinate).

Since D should be vertically aligned with A (same x-coordinate) and horizontally aligned with C (same y-coordinate):

The x-coordinate of D should be the same as A's x-coordinate: x = 3.

The y-coordinate of D should be the same as C's y-coordinate: y = 5.

Thus, the coordinates of the fourth vertex D are: D(3,5)

Verification

AB: Horizontal side, distance ∣3−(−4)∣ = 7

BC: Vertical side, distance ∣2−5∣ = 3

CD: Horizontal side, distance ∣3−(−4)∣ = 7

DA: Vertical side, distance ∣2−5∣ = 3

All side lengths match, confirming the shape is a rectangle. Thus, the coordinates (3,5) are correct.

8. Solution: (i) Point A is at coordinates (1, -1).

Point B is at coordinates (4, 5).

Draw a straight line joining points A and B.

A simple approach is to use the midpoint formula to find a point between A and B.

The midpoint M of line segment joining x1,y1 and x2,y2 can be found as follows:

M = x1+x22,y1+y22

Putting A(1,-1) and B(4,5): M = 1+42,−1+52 = 2.5,2

Therefore, the coordinates of the point on the line segment AB between A and B are 2.5,2

(ii) Extend the line segment and find a point outside the line segment:

The slope m of the line passing through A(1,−1) and B(4,5) is given by

m = y2−y1x2−x1 = 5−−14−1 = 63 = 2.

A point P that lies on the extended line can be chosen by increasing the x-coordinate by a certain amount. Let's choose a point with x-coordinate of 6 (2 units beyond B).

Using the slope m = 2: y2−y1 = 2x2−x1 ⟹ y−5 = 2x−4

Substituting x = 6:

y − 5 = 2(6−4) = 2(2) = 4

y = 5 + 4 = 9

Therefore, the coordinates of a point on the extended line are (6,9).

Q1

Imagine a town planning committee is designing a new park. The park is in the shape of a triangle with vertices at coordinates A(−3,2), B(1,−4), and C(x,y). The committee wants to place a fountain at point F inside the park such that the distances from F to the vertices A, B, and C are equal.

1. Determine the coordinates (x,y) of vertex C such that triangle ABC is isosceles with AB = AC.

2. Suppose the committee decides to plant trees along the sides of △ABC. Determine the coordinates of the midpoint of side AB to optimize tree placement.

3. If the area of △ABC is 24 square units, find the coordinates of the centroid G of the triangle.

Sol

Solution:

Let's solve each part of the question step by step:

1. Determine the coordinates (x,y) of vertex C such that triangle ABC is isosceles with AB = AC.

For triangle ABC to be isosceles with AB = AC, point C must be equidistant from points A and B. This means C lies on the perpendicular bisector of AB.

Calculate the midpoint of AB:

Midpoint of AB = (−3+12, 2−42) = (−1,−1)

Find the equation of the perpendicular bisector of AB, which passes through the midpoint (−1,−1) and has a slope perpendicular to AB.

Slope of AB = −4−21+3 = −64 = −32

Thus, slope of perpendicular bisector = 23

Using the point-slope form:

y+1=23x+1

y=23x−13

Distance formula for AC: AC = x+32+y−22

Distance formula for AB: AB = 1−−32+−4−22 = 42+−62

= 16+36 = 52 = 213

Since, we need AC = AB

x+32+y−22 = 213

Substitute y value into the equation and square both sides to remove the roots.

x+32+23x−732 = 52

Upon expanding and simplifying:

9x2+6x+9+4x2−14x+49=468

13x2+40x−338=0

Finding the roots of the above equation in the formula −b±b2−4ac2a,

we get x = 3.78 and -6.86 (ignore negative value as location coordinates in a park can't be negative)

Putting x = 3.78 in equation for y: y = 233.78−13 = 2.19

Therefore, the coordinates of vertex C are approximately (3.78,2.19). These coordinates satisfy the condition that triangle ABC is isosceles with AB = AC.

2. The midpoint M of AB is already calculated: M = (−1,−1)

3. The centroid G divides each median of the triangle in a 2:1 ratio from the vertex.

Calculate the coordinates of the centroid G:

G(x) = x1+x2+x33 and G(y) = y1+y2+y33

Substituting A(−3,2), B(1,−4), C(x,y): ​ G(x) = −3+1+x3 = x−23 -(A) ​ G(y) = 2−4+y3 = y−23 - (B)

Also given Area of triangle = 12x1y2−y3+x2y3−y1+x3y1−y2 = 24

Substituting A(−3,2), B(1,−4), C(x,y):

48 = 15 + 3y + 6x - (C)

Now, solve for x and y using the above equation and the condition that F (the point where distances to vertices are equal) is at the centroid G:

x−23 = y−23

x = y

Putting this in eqn(C) :

48 = 15 + 9x

x = 339 = 113

Since y = x, we have x = 113 and y = 113.

​Putting this in eqn (A) and (B):

G(x) = 59 and G(y) = 59