Arithmetic Progression

Here are a few more exercises. Can you find the slope and y-intercept in each case, and write down the equation of the line?

Many professions that use mathematics are interested in one specific aspect – finding patterns, and being able to predict the future. Here are two examples:

Geologists around the world want to predict earthquakes and volcano eruptions. They can try to find patterns in historical data of from seismographs, of the atmosphere, or even animal behaviour. One earthquake, for example, might trigger aftershocks later.

Bankers also look at historical data of stock prices, interest rates and currency exchange rates to estimate how financial markets might change in the future. Being able to predict if the value of a stock will go up or down can be extremely lucrative!

Professional mathematicians use highly complex algorithms to find and analyse all these patterns, but for now, let’s start with something much simpler.

Simple Sequences

In mathematics, a sequence is a chain of numbers (or other objects) that usually follow a particular pattern. The individual elements in a sequence are called terms.

Here are a few examples of sequences. Can you find their patterns and calculate the next two terms?

3, 6 +3, 9 , 12 , 15 , , … Pattern: “Add 3 to the previous number to get the next one.”

4, 10 , 16 , 22 , 28 , , , … Pattern: “Add 6 to the previous number to get the next one.”

3, 4 , 7 , 8 , 11 , , , … Pattern: “Alternatingly add 1 and add 3 to the previous number, to get the next one.”

1, 2 , 4 , 8 , 16 , , , … Pattern: “Multiply the previous number by 2, to get the next one.”

The dots (…) at the end simply mean that the sequence can go on forever. When referring to sequences like this in mathematics, we often represent every term by a special variable:

x1, …x2, …x3, …x4, …x5, …x6, …x7, …

The small number after the x is called a subscript, and indicates the position of the term in the sequence. This means that we can represent the nth term in the sequence by .

Triangle and Square Numbers

Sequences in mathematics don’t always have to be numbers. Here is a sequence that consists of geometric shapes – triangles of increasing size:

At every step, we’re adding one more row to the previous triangle. The length of these new rows also increases by one every time. Can you see the pattern?

1, 3 +2, 6 +3, 10 +4, 15 +5, 21 +6 +7, +8, …

We can also describe this pattern using a special formula:

xn = xn−1 + n

To get the n-th triangle number, we take the triangle number and add n. For example, if n = ${n}, the formula becomes x${n}=x${n-1}+${n}.

A formula that expresses xn as a function of previous terms in the sequence is called a recursive formula. As long as you know the in the sequence, you can calculate all the following ones.

Another sequence which consists of geometric shapes are the square numbers. Every term is formed by increasingly large squares:

For the triangle numbers we found a recursive formula that tells you the next term of the sequence as a function of of its previous terms. For square numbers we can do even better: a formula that tells you the nth term directly, without first having to calculate all the previous ones:

xn =

This is called an explicit formula. We can use it, for example, to calculate that the 13th square number is , without first finding the previous 12 square numbers.

Let’s summarise all the definitions we have seen so far:

A sequence is a list of numbers, geometric shapes or other objects, that follow a specific pattern. The individual items in the sequence are called terms, and represented by variables like xn.

A recursive formula for a sequence tells you the value of the nth term as a function of . You also have to specify the first term(s).

An explicit formula for a sequence tells you the value of the nth term as a function of , without referring to other terms in the sequence.

Action Sequence Photography

In the following sections you will learn about many different mathematical sequences, surprising patterns, and unexpected applications.

First, though, let’s look at something completely different: action sequence photography. A photographer takes many shots in quick succession, and then merges them into a single image:

Can you see how the skier forms a sequence? The pattern is not addition or multiplication, but a geometric transformation. Between consecutive steps, the skier is both translated and .

Here are a few more examples of action sequence photography for your enjoyment:

In 1682, the astronomer Edmond Halley observed an unusual phenomenon: a glowing white object with a long tail that moved across the night sky. It was a comet, a small, icy rock that is flying through space, while leaving behind a trail of dust and ice.

Halley remembered that other astronomers had observed similar comets much earlier: one in 1530 and another in 1606. Notice that the gap between two consecutive observations is the same in both cases: years.

Image of Halley’s Comet,
taken in 1986 on Easter Island

Halley concluded that all three observations were in fact of the same comet – which is now called Halley’s comet. It is orbiting around the sun and passes Earth approximately every 76 years. He also predicted when the comet would be visible next:

1530, 1606 +76, 1682 +76, 1758 +76, +76, +76, +76, …

Actually, the time interval is not always exactly 76 years: it can vary by one or two years, as the comet’s orbit is interrupted by other planets. Today we know that Halley’s comet was observed by ancient astronomers as early as 240 BC!

Depictions of Halley’s comet throughout time: a Babylonian tablet (164 BC), a medival tapestry (1070s), a science magazine (1910) and a Soviet stamp (1986).

A different group of scientists is investigating the behaviour of a bouncing tennis ball. They dropped the ball from a height of 10 meters and measured its position over time. With every bounce, the ball loses some of its original height:

The scientists noticed that the ball loses 20% of its height after every bounce. In other words, the maximum height of every bounce is 80% of the previous one. This allowed them to predict the height of every following bounce:

10, 8 ×0.8, ×0.8, ×0.8, 4.096 ×0.8, 3.277 ×0.8, 2.621 ×0.8, 2.097 ×0.8, …

If you compare both these problems, you might notice that there are many similarities: the sequence of Halley’s comet has the same between consecutive terms, while the sequence of tennis ball bounces has the same between consecutive terms.

Sequences with these properties have a special name:

An arithmetic sequence has a constant difference d between consecutive terms.

The same number is added or subtracted to every term, to produce the next one.

A geometric sequence has a constant ratio r between consecutive terms.

Every term is multiplied or divided by the same number, to produce the next.

Here are a few different sequences. Can you determine which ones are arithmetic, geometric or neither, and what the values of d and r are?

2, 4, 8, 16, 32, 64, …

is , with ratio .

2, 5, 8, 11, 14, 17, …

is , with difference .

17, 13, 9, 5, 1, –3, …

is , with difference .

2, 4, 7, 11, 16, 22, …

is .

40, 20, 10, 5, 2.5, 1.25, …

is , with ratio .

To define an arithmetic or geometric sequence, we have to know not just the common difference or ratio, but also the initial value (called a). Here you can generate your own sequences and plot their values on a graph, by changing the values of a, d and r. Can you find any patterns?

Arithmetic Sequence

a = ${a}, d = ${d}

${arithmetic(a,d,0)}, ${arithmetic(a,d,1)}, ${arithmetic(a,d,2)}, ${arithmetic(a,d,3)}, ${arithmetic(a,d,4)}, ${arithmetic(a,d,5)}, …

Geometric Sequence

a = ${b}, r = ${r}

${geometric(b,r,0)}, ${geometric(b,r,1)}, ${geometric(b,r,2)}, ${geometric(b,r,3)}, ${geometric(b,r,4)}, ${geometric(b,r,5)}, …

Notice how all arithmetic sequences look very similar: if the difference is positive, they steadily , and if the difference is negative, they steadily .

Geometric sequences, on the other hand, can behave completely differently based on the values of a and r:

If , the terms will , up to infinity. Mathematicians say that the sequence diverges.

If , the terms will always . We say that the sequence converges.

If , the terms will alternate between positive and negative, while their gets bigger.

You’ll learn more about convergence and divergence in the last section of this course.

Recursive and Explicit Formulas

In the previous section, you learned that a recursive formula tells you the value of each term as a function of previous terms. Here are the recursive formulas for arithmetic and geometric sequences:

xn=

One problem with recursive formulas is that to find the 100th term, for example, we first have to calculate the previous 99 terms – and that might take a long time. Instead, we can try to find an explicit formula, that tells us the value of the nth term directly.

For arithmetic sequences, we have to add d at every step:

x1= a

x2= a+d

x3= a+d+d

x4=

x5=

At the nth term, we are adding copies of d, so the general formula is

xn=a+d×n−1.

For geometric sequences, we have to multiply r at every step:

x1=a

x2=a×r

x3=a×r×r

x4=

x5=

At the nth term, we are multiplying copies of r, so the general formula is

xn=a×rn−1.

Here is a summary of all the definitions and formulas you’ve seen so far:

An arithmetic sequence has first term a and common difference d between consecutive terms.

Recursive formula: xn=xn−1+d

Explicit formula: xn=a+d×n−1

A geometric sequence has first term a and common ratio r between consecutive terms.

Recursive formula: xn=xn−1×r

Explicit formula: xn=a×rn−1

Now let’s have a look at some examples where we can use all this!

Pay it Forward

Here is a short clip from the movie Pay it Forward, where 12-year-old Trevor explains his idea for making the world a better place:

The essence of Trevor’s idea is that, if everyone “pays it forward”, a single person can have a huge impact on the world:

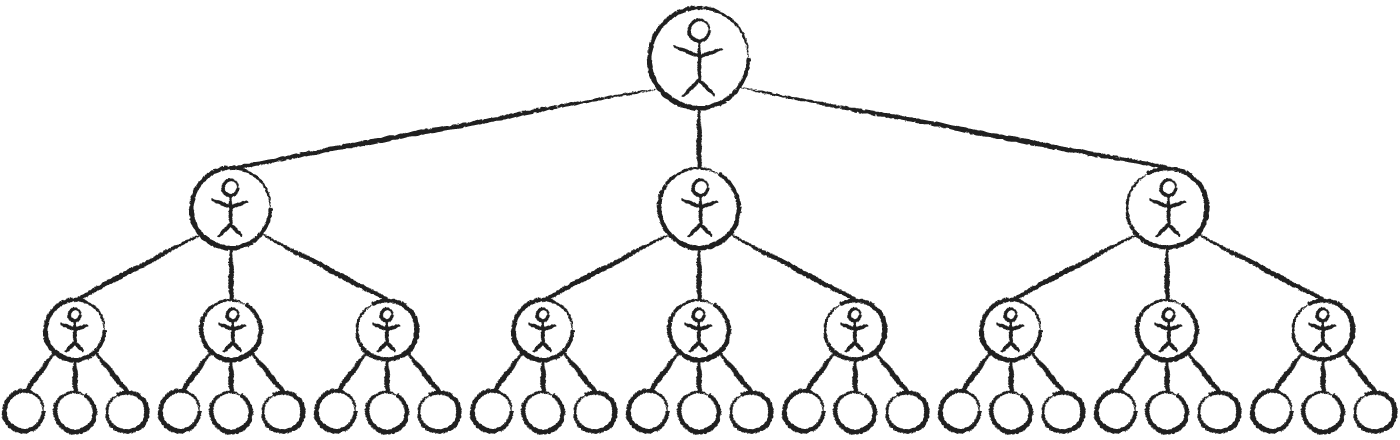
Notice how the number of people at every step forms a , with common ratio :

1, 3 ×3, 9 ×3, ×3, ×3, ×3, …

Using the explicit formula for geometric sequences, we can work out how many new people are affected at any step:

xn =

The number of people increases incredibly quickly. In the 10th step, you would reach 19,683 new ones, and after 22 steps you would have reached more people than are currently alive on Earth.

This sequence of numbers has a special name: the powers of 3. As you can see, every term is actually just a different power of 3:

30, 31, 32, 33, 34, 35, …

Who wants to be a Millionaire?

COMING SOON!

The Chessboard Problem