Pairs of Angles
Concerning angles, we know about complementary angles, supplementary angles, adjacent angles, linear pair of angles etc. Now, let's move on to finding out about angles formed when a ray is placed on a line.
What are the angles formed at the point Q? They are ∠ PQS, ∠ SQR and ∠ PQR.
Can we write ∠ PQS + ∠ SQR = ∠ PQR?
What is the measure of ∠ PQR? It is
From (1) and (2), we can now say that-
∠ PQS + ∠ SQR = 180°
From here, we can state the following Axiom:
Axiom: If a ray stands on a line, then the sum of two adjacent angles so formed is 180°
Since, here the sum of measures of the two adjacent angles is equal to 180°, they are together called a linear pair of angles.
Now, is the converse of this statement true? i.e.
If the sum of two adjacent angles is 180°, then a ray stands on a line aka the non-common arms form a line?
Upon examining multiple pairs of angles with different mesures- as it turns out, it is in fact true. Thus,
Axiom: If the sum of two adjacent angles is 180°, then the non-common arms of the angles form a line.
The two axioms that we have just studied together are known as the Linear Pair Axiom.
Moving on to the next situation where two lines intersect at a common point. We know that when two lines intersect, the vertically opposite angles are equal. So, let's prove it now.
Theorem : If two lines intersect each other, then the vertically opposite angles are equal.
Proof : Let lines AB and CD intersect at O as shown above. This leads to the formation of two pairs of vertically opposite angles
(i) ∠ AOC and ∠ BOD
(ii) ∠ AOD and ∠ BOC
We need to prove that: ∠ AOC = ∠ BOD and ∠ AOD = ∠ BOC
- We can say that
OA stands on line CD - Using linear pair axiom we get
- Similarly, ray
stands on line AB - Again using linear pair axiom we get
- From (1) and (2) together
- Thus, we get: ∠ AOC = ∠
- Similarly, we can conclude: ∠AOD = ∠
Example 1 : In the below figure, lines PQ and RS intersect each other at point O. If ∠ POR : ∠ ROQ = 5 : 7, find all the angles.
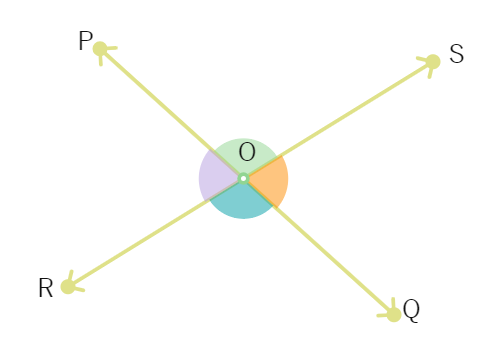
Solution : ∠ POR + ∠ROQ =
But ∠ POR : ∠ ROQ = 5 : 7 (Given)
Therefore, ∠ POR =
Similarly, ∠ ROQ =
Now, ∠ POS =
and ∠ SOQ =
Example 2: In the below figure, ray OS stands on a line POQ. Ray OR and ray OT are angle bisectors of ∠ POS and ∠ SOQ, respectively. If ∠ POS = x, the ∠ ROT is equal to :
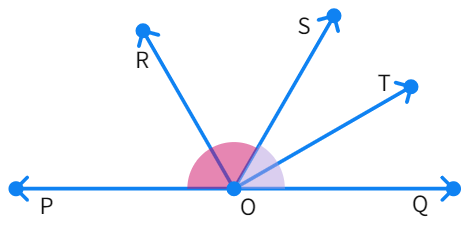
- By linear pair axiom: ∠ POS + ∠ SOQ =
° - As ∠ POS = x we get: ∠ SOQ = 180° – x
- Given that: OR and OT bisect the angles ∠ POS and ∠ SOQ.
- Thus, ∠ ROS =
° while ∠ SOT = ° - We see that: ∠ ROT = ∠ ROS + ∠
- Thus, ∠ ROT =
° - Substituting values
- We have found the answer
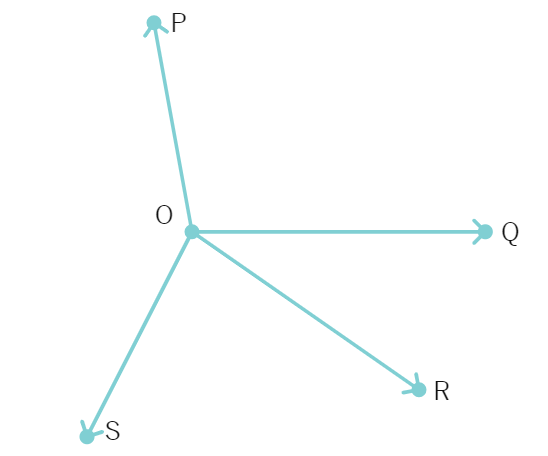
Example 3 : In the given figure, OP, OQ, OR and OS are four rays. Prove that ∠ POQ + ∠ QOR + ∠ SOR + ∠ POS = 360°.
Solution : In the figure, you need to produce any of the rays OP, OQ, OR or OS backwards to a point. Let us produce ray OQ backwards to a point T so that TOQ is a line (as shown below).
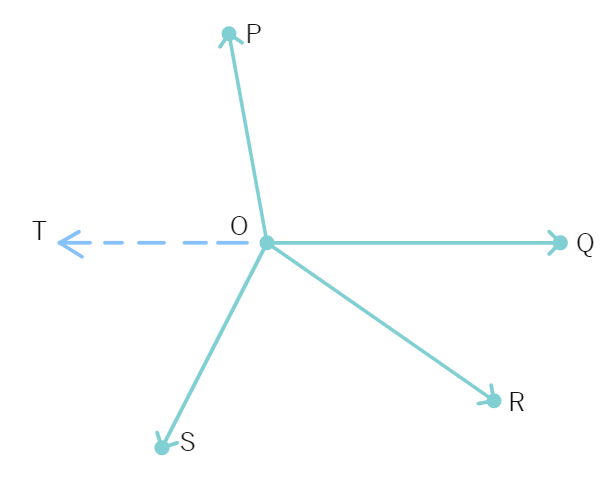
Now, ray OP stands on line TOQ.
Therefore, ∠TOP +
Similarly, ray OS stands on line TOQ.
Therefore, ∠TOS +
But ∠ SOQ = ∠ SOR +
So, (2) becomes ∠ TOS + ∠ SOR + ∠ QOR =
Now, adding (1) and (3), you get:
∠ TOP + ∠ POQ + ∠ TOS + ∠ SOR + ∠ QOR =
But ∠ TOP + ∠ TOS = ∠
Therefore, (4) becomes ∠ POQ + ∠ QOR + ∠ SOR + ∠ POS =
