Some More Interesting Patterns

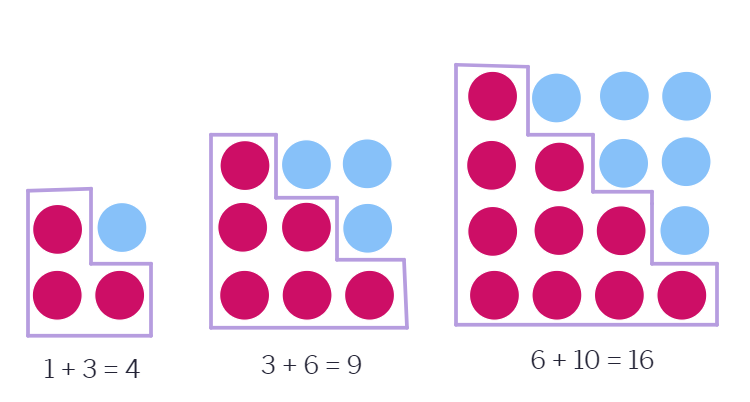
Adding triangular numbers.

Do you remember triangular numbers (numbers whose dot patterns can be arranged as triangles)?

If we combine two consecutive triangular numbers, we get a square number, like:

Numbers between square numbers

Let us now see if we can find some interesting pattern between two consecutive square numbers.

1	=	12
2, 3, 4	=	22	non square numbers between the two square numbers 1 (=12) and 4 (=22)
5, 6, 7, 8, 9	=	32	non square numbers between the two square numbers 4 (=22) and 9 (=32)
10, 11, 12, 13, 14, 15, 16	=	42	non square numbers between the two square numbers 9 (=32) and 16 (=42)
17, 18, 19, 20, 21, 22, 23, 24, 25	=	52	non square numbers between the two square numbers 16 (=22) and 25 (=52)

Between 12(=1) and 22(= 4), there are two (i.e., 2 × 1) non square numbers 2, 3.

Between 22(= 4) and 32(= 9), there are four (i.e., 2 × 2) non square numbers 5, 6, 7, 8.

Now, 32 = 9, 42 =

Therefore, 42 – 32 = 16 – 9 =

Between 9(=32) and 16(= 42): the numbers are 10, 11, 12, 13, 14, 15 that is, six non-square numbers which is 1 less than the difference of two squares.

We have 42 = and 52 =

Therefore, 52 – 42 =

Between 16(= 42) and 25(= 52) the numbers are 17, 18, ... , 24 that is, eight non square numbers which is 1 less than the difference of two squares.

Consider 72 and 62. Can you say how many numbers are there between 62 and 72?

If we think of any natural number n and (n + 1), then:

n+12 – n2 = n2+2n+1−n2=2n+1

We find that between n2 and n+12 there are 2n numbers which is 1 less than the difference of two squares.

Thus, in general we can say that there are 2n between the squares of the numbers n and (n + 1).

Try These

1(a)

How many natural numbers lie between 92 and 102? Between 112 and 122 ?

(a) 92= and 102 =

The natural numbers between 81 and 100 are 82, 83, 84 ....... , 99.

To count these, subtract the smaller number from the larger number and 1:

100 − 81 − 1 =

So, there are 18 natural numbers between 92 and 102.

1(b)

(b) 112 = and 122 =

The natural numbers between 121 and 144 are 122, 123, ...... 143.

Which gives us: 144 − 121 − 1 =

So, there are 22 natural numbers between 112 and 122.

2(i)

2. How many non square numbers lie between the following pairs of numbers: (i) 1002 and 1012 (ii) 902 and 912 (iii) 10002 and 10012

To determine how many non-square numbers lie between two consecutive perfect squares n2 and n+12, use the following method:

The total number of natural numbers between n2 and n+12 is n+12 − n2 -1 = .

Since only one number between n2 and n+12 can be a perfect square (specifically n+12), the number of non-square numbers is 2n−1.

(i) Between 1002 and 1012: n =

The total number of natural numbers between them is 2 × 100 = .

Number of non-square numbers = 200 − 1 = .

2(ii)

(ii) Between 902 and 912: n =

The total number of natural numbers between them is 2 × 90 = .

Number of non-square numbers = 180 − 1 = .

2(iii)

(iii) Between 10002 and 10012: n =

The total number of natural numbers between them is 2 × 1000 = .

Number of non-square numbers = 2000 − 1 = .

Adding odd numbers

Consider the following:

1 one odd number	= 1 = 12
1 + 3 sum of first two odd numbers	= = 22
1 + 3 + 5 sum of first three odd numbers	= = 32
1 + 3 + 5 + 7 sum of first odd numbers	= = 42
1 + 3 + 5 + 7 + 9 sum of first odd numbers	= = 52
1 + 3 + 5 + 7 + 9 + 11 sum of first odd numbers	= = 62

So, we can say that the sum of first n odd natural numbers is n2.

Looking at it in a different way, we can say: ‘If the number is a square number, it has to be the sum of successive odd numbers starting from 1.

Consider those numbers which are not perfect squares, say 2, 3, 5, 6, ... . Can you express these numbers as a sum of successive odd natural numbers beginning from 1? (Yes/No)

You will find that these numbers cannot be expressed in this form.

Consider the number 25 (see below pattern):

25 , 24 , 21 ,16 , , Pattern: “Successively subtract 1, 3, 5, 7, 9, ... from it, to get the next one.”

This means, 25 = 1 + 3 + 5 + 7 + 9. Also, 25 is a perfect square.

Now consider another number 38, and again do as above.

38 , 37 , 34 ,29 , 22 , ,,
Pattern: “Successively subtract 1, 3, 5, 7, 9, ... from it, to get the next one.”

This shows that we are not able to express 38 as the sum of consecutive odd numbers starting with 1. Also, 38 is not a perfect square.

So we can also say that if a natural number cannot be expressed as a sum of successive odd natural numbers starting with 1, then it is not a perfect square.

We can use this result to find whether a number is a perfect square or not.

Find whether each of the following numbers is a perfect square or not?

Instructions

121

Perfect Square

Not a Perfect Square

A sum of consecutive natural numbers

Consider the following:

32 = 9 = 4 + 5

52 = 25 = 12 + 13

72 = 49 = 24 +

92 = 81 = + 41

112= 121 = 60 +

152 = 225 = +

Q1

1. Express the following as the sum of two consecutive integers:

(i) 212 (ii) 132 (iii) 112 (iv) 192

So, for a number to be expressed as the sum of two consecutive integers, it must be of the form 2n+1, which means it must be an number.

All of the above numbers are even. Which means they cannot be expressed as the sum of two consecutive integers. Only odd numbers can be expressed as the sum of two consecutive integers.

Therefore, of the given numbers can be expressed as the sum of two consecutive integers.

Q2

2. Do you think the reverse is also true, i.e., is the sum of any two consecutive positive integers is perfect square of a number? Give example to support your answer.

The sum of any two consecutive positive integers is not always a perfect square.

Explanation:

Let the two consecutive positive integers be n and n+1. Their sum is: n+n+1 = .

This sum, 2n+1, is always an number.

However, for it to be a perfect square: it must be equal to the square of some integer, say m2.

So, we are asking whether there exists an integer m such that: m2 = 2n+1

This equation can be rearranged to: 2n=m2−1

n = m2−12 . Now, for n to be an integer, m2−1 must be , which means m must be .

However, even when m is odd, not all values of 2n+1 are perfect squares.

Consider the consecutive integers 2 and 3: 2 + 3 =

5 is not a perfect square. Therefore, the sum of these consecutive integers a perfect square.

Consider another pair of consecutive integers 8 and 9: 8 + 9 =

17 is not a perfect square either.

Thus, the sum of two consecutive positive integers is not always a perfect square.

Product of two consecutive even or odd natural numbers

11 × 13 = 143 = 122 – 1

Also:

11 × 13 = (12 – 1) × (12 + 1)

Therefore,

11 × 13 = (12 – 1) × (12 + 1) = 122 – 1

Similarly,

13 × 15 = ( – 1) × ( + 1) = 142 – 1

× = (30 – 1) × (30 + 1) = 302 – 1

44 × = (45 – 1) × ( + 1) = 452 – 1

So in general, we can say that:

(a + 1) × (a – 1) = a2 – 1

Some more patterns in square numbers

Observe the squares of numbers; 1, 11, 111 ... etc. They give a beautiful pattern:

12 =	1
112 =	1 2 1
1112 =	1 2 2 1
11112 =	1 2 2 1
111112 =	2 4 4 2
111111112 =	1 2 3 4 4 3 2 1

Another interesting pattern

72	= 49
672	= 4489
6672	= 444889
66672	= 44448889
666672	= 4444488889
6666672	= 444444888889

The fun is in being able to find out why this happens. May be it would be interesting for you to explore and think about such questions even if the answers come some years later.

Write the square, making use of the above pattern:

(i) 1111112 (ii) 11111112

Applying the Pattern to the Given Numbers:

1111112 =

11111112=

Can you find the square of the following numbers using the above pattern?

(i) 66666672 (ii) 666666672

66666672 =

666666672 =

Squares and Square Roots

Glossary

Some More Interesting Patterns

Try These

1(a)

1(b)

2(i)

2(ii)

2(iii)

Q1

Q2

Sign in to Innings2

Squares and Square Roots

Reset Progress

Glossary

Some More Interesting Patterns

Try These

1(a)

1(b)

2(i)

2(ii)

2(iii)

Q1

Q2