Exercise 6.3

1. State which pairs of triangles in Fig, are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :

(i)

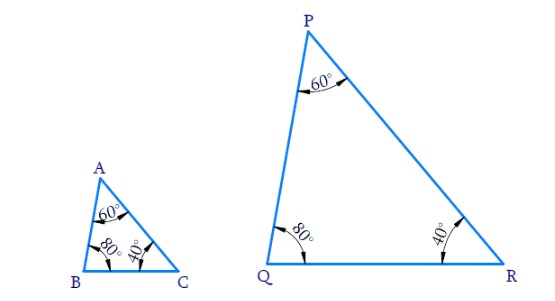
In ΔABC and ΔPQR

∠A = ∠P = °

∠B = ∠Q = °

∠C = ∠R = °

All the corresponding angles of the triangles are .

By AAA criterion ΔABC ∼ ΔPQR

(ii)

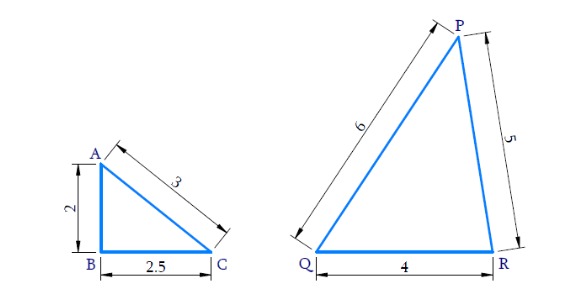
In ΔABC and ΔQRP,

ABQR = 24 =

BCPR = 2.55 =

ACPQ = 36 =

⇒ ABQR = BCPR = ACPQ =

All the corresponding sides of the two triangles are in the same proportion.

By SSS criterion ΔABC ∼ ΔQPR

(iii)

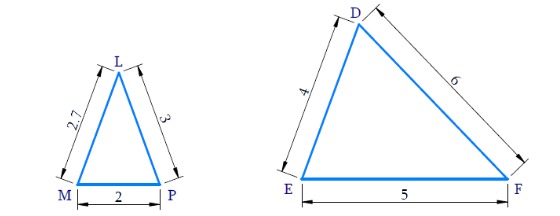
In ΔLMP and ΔFED,

LMFE =

MPED = 24 =

LPFD = 36 =

⇒LMFE ≠ MP = LPFD

All the corresponding sides of the two triangles are not in the same proportion.

Hence triangles are not similar. ΔLMP ≠ ΔFED

(iv)

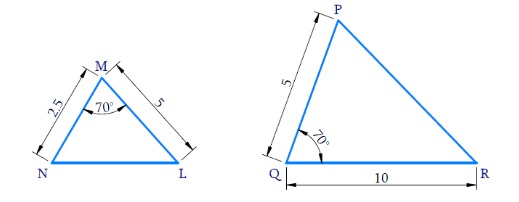
In ΔNML and ΔPQR,

NMPQ = 2.55 =

MLQR = 510 =

⇒ NMPQ = MLQR =

∠M = ∠Q = °

One angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional.

By SAS criterion ⇒ ΔNML ∼ ΔPQR

(v)

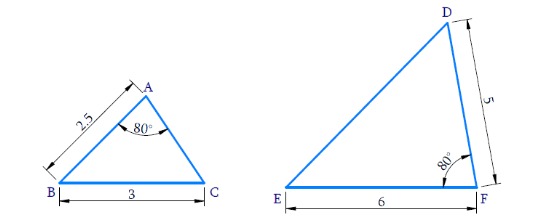
In ΔABC and ΔDFE,

ABDF = 2.55 =

BCEF = 36 =

ABDF = BCEF =

∠A = ∠F = °

But ∠B must be equal to °

The sides AB, BC includes ∠B , not ∠A

Therefore, SAS criterion is not satisfied

Hence, the triangles are not similar, ΔABC ≠ ΔDFE

(vi)

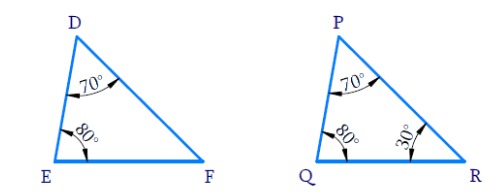
In ΔDEF,

∠D = °, ∠E = °

⇒ ∠F = ° [∵ Sum of the angles in a triangle is °]

Similarly, In ΔPQR ∠Q = ° , ∠R = °

⇒ ∠P = °

In ΔDEF and ΔPQR,

∠D = ∠P = °

∠E = ∠Q = °

∠F = ∠R = °

All the corresponding angles of the triangles are .

By AAA criterion ΔDEF ∼ ΔPQR

2. In Fig, ∆ ODC ~ ∆ OBA, ∠ BOC = 125° and ∠ CDO = 70°. Find ∠ DOC, ∠ DCO and ∠ OAB

Solution:

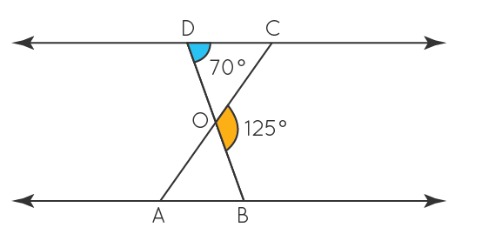
In the given figure,

∠DOC = ° - ∠COB [∵ ∠DOC and ∠COB form a pair]

∠DOC = 180° - °

∠DOC = °

In ΔODC, ∠DCO = 180° - (∠DOC + ∠ODC) [angle sum property of a triangle]

∠DCO = ° - (° + °)

∠DCO = 180° - °

∠DCO = °

In ΔODC and ΔOBA

ΔODC ∼ Δ (given)

⇒ ∠OCD = ∠

Thus, ∠OAB = 55°

3. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that OAOC = OBOD

Solution:

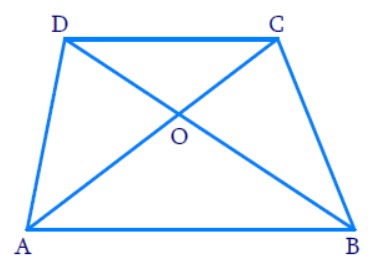
In ΔAOB and ΔCOD,

∠AOB = ∠ ( angles)

∠BAO = ∠ ( angles)

⇒ ΔAOB ∼ Δ (AA criterion)

Hence, OAOC = OBOD

4. In Fig, QRQS = QTPR and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR

Solution:

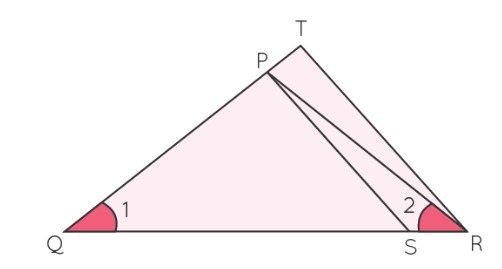
In ΔPQR, ∠1 = ∠

⇒ PR = (In a triangle, sides opposite to equal angles are )

In ΔPQS and ΔTQR:

∠PQS = ∠TQR = ∠ (same angle)

QRQS = (Since PR = )

⇒ ΔPQS ~ Δ ( criterion)

5. S and T are points on sides PR and QR of ∆PQR such that ∠P = ∠RTS. Show that ΔRPQ ~ ΔRTS

Solution:

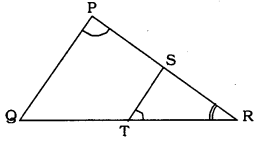
In ΔRPQ and ΔRTS,

∠RPQ = ∠ (given)

∠PRQ = ∠ ( angle)

Thus, ΔRPQ ∼ Δ (AA criterion)

6. In Figure, if ∆ABE ≅ ∆ACD, show that ∆ADE ~ ∆ABC.

Solution:

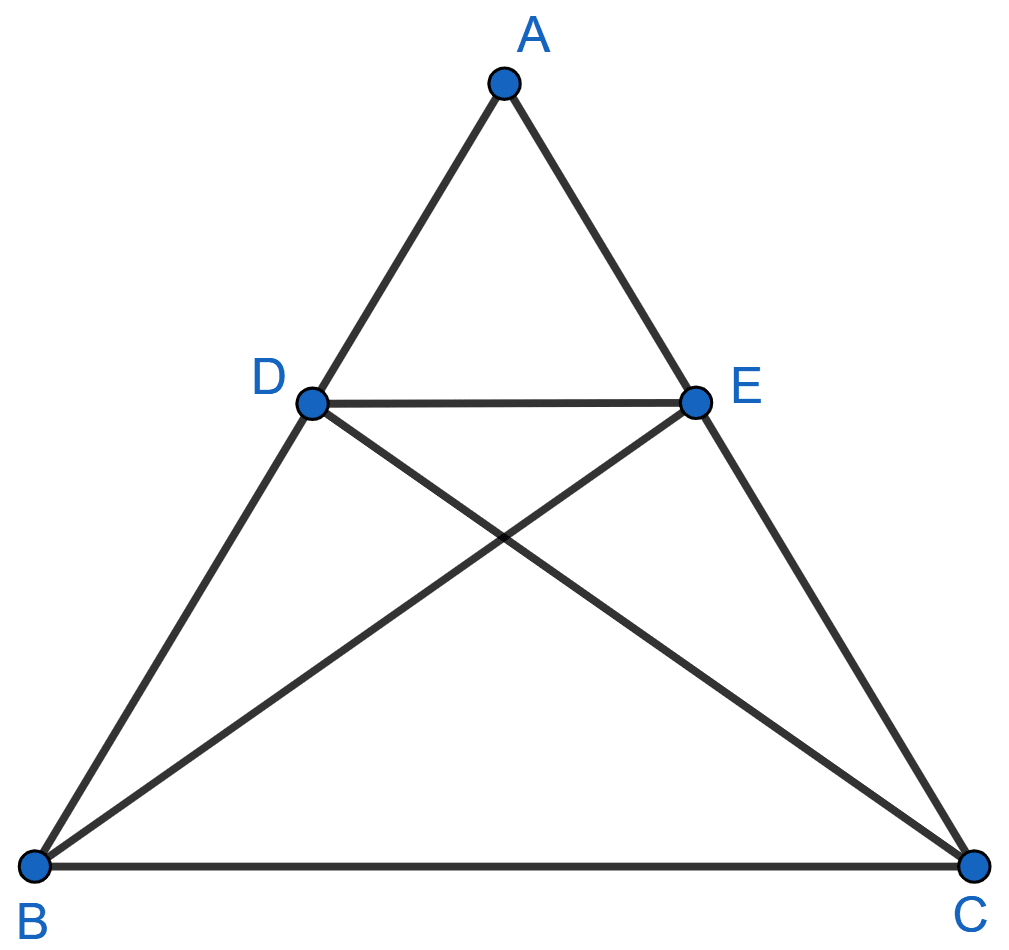
In ∆ABE and ∆ACD:

AD = (∆ABE ≅ ∆ACD given).......... (1)

AB = (∆ABE ≅ ∆ACD given)......... (2)

Now consider ∆ADE and ∆ABC:

ADAB = [From equations (1) and (2)]

and ∠DAE = ∠ (Common angle)

Thus, ∆ADE ~ ∆ (SAS criterion)

7. In Fig, altitudes AD and CE of Δ ABC intersect each other at the point P. Show that:

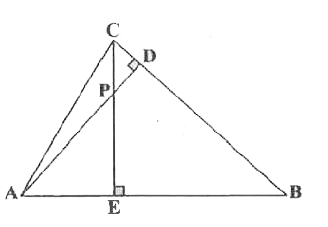
(i)

(i) ΔAEP ~ ΔCDP

Solution:

In ΔAEP and ΔCDP,

∠AEP = ∠ = º

[∵ CE ⊥ AB and AD ⊥ BC; ]

∠APE = ∠ ( angles)

⇒ ΔAEP ΔCPD (AA criterion)

(ii)

(ii) ΔABD ~ ΔCBE

Solution:

In ΔABD and ΔCBE:

∠ADB = ∠ = º

∠ABD = ∠ ( angle)

⇒ ΔABD ΔCBE (AA criterion)

(iii)

(iii) ΔAEP ~ ΔADB

Solution:

In ΔAEP and ΔADB:

∠AEP = ∠ADB = º

∠PAE = ∠ ( angle)

⇒ ΔAEP ΔADB (AA criterion)

(iv)

(iv) ΔPDC ~ ΔBEC

Solution:

In ΔPDC and ΔBEC:

∠PDC = ∠BEC = º

∠PCD = ∠ ( angle)

⇒ ΔPDC ~ Δ ( AA criterion)

8. E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ~ ΔCFB

Solution:

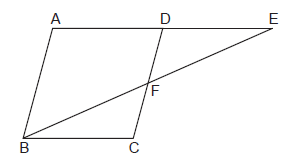
In ΔABE and ΔCFB,

∠BAE = ∠ ( angles of a parallelogram)

∠AEB = ∠ [AE || BC and EB is a transversal, alternate interior angles]

Thus, ΔABE ~ Δ (AA criterion)

9. In Fig, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:

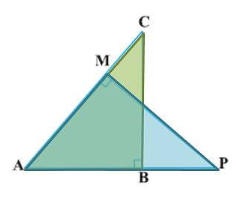
(i)

(i)ΔABC ~ ΔAMP

Solution:

In ΔABC and ΔAMP:

∠ABC = ∠ = º

∠BAC = ∠ ( angle)

Thus, ΔABC ∼ Δ (AA criteria)

(ii)

(ii)CAPA = BCMP

Solution:

In ΔABC and ΔAMP,

CAPA = [∵ ΔABC ∼ ΔAMP]

10. CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ABC and ∆EFG respectively. If ∆ABC ~ ∆FEG, show that:

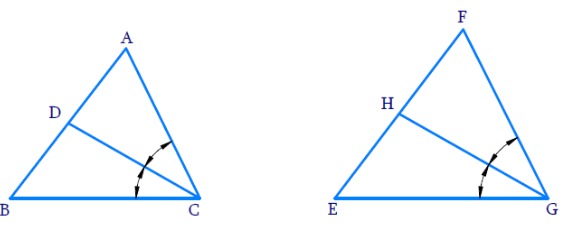
(i)

(i)CDGH = ACFG

Solution:

∠ACB = ∠ (Given that ∆ABC ~ ∆FEG)

⇒ ∠ACB2 = ∠FGE2

⇒ ∠ACD = ∠ (CD and GH are of ∠C and ∠G respectively) (1)

In ∆ADC and ∆FHG:

∠DAC = ∠ [∆ADC ~ ∆FEG]

∠ACD = ∠ [From equation (1)]

Thus, ∆ADC ~ ∆ (AA criterion)

⇒ CDGH = [If two triangles are similar, then their corresponding sides are in the same ratio]

(ii)

(ii)∆DCB ~ ∆HGE

Solution:

In ∆DCB and ∆HGE:

∠DBC = ∠ [∆ABC ~ ∆FEG]

∠DCB = ∠ [∵ ∠ACB2 = ∠FGE2]

Thus, ∆DCB ∆HGE (AA criterion)

(iii)

(iii) ∆DCA ~ ∆HGF

Solution:

In ∆DCA and ∆HGF:

∠DAC = ∠ [∆ABC ~ ∆FEG]

∠ACD = ∠ [∵ ∠ACB = ∠FGE]

Thus, ∆DCA ~ ∆ (AA criterion)

11. In Fig, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ∆ ABD ~ ∆ ECF

Solution:

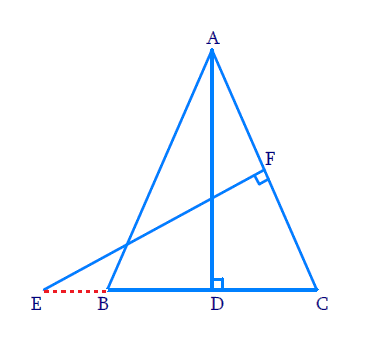
In ΔABD and ΔECF:

∠ADB = ∠EFC = º [∵ AD ⊥ and EF ⊥ ]

∠ABD = ∠ [∵ In ΔABC, AB = AC which signifies ∠ABC = ∠ACB as angles opposite to equal sides are ]

Thus we have ΔABD ΔECF (AA criterion)

12. Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ∆ PQR (see Fig.). Show that ∆ ABC ~ ∆ PQR

Solution:

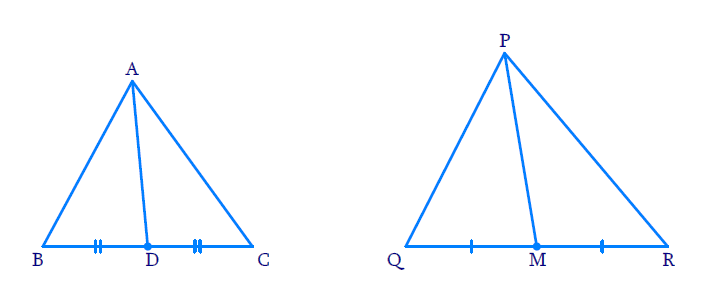
In ΔABC and ΔPQR:

ABPQ = BCQR = (given)

AD and PM are of ΔABC and ΔPQR respectively.

⇒ BDQM = (BC/2)(QR/2) =

Now, in ΔABD and ΔPQM

ABPQ = BDQM =

⇒ ΔABD ∼ Δ [SSS criterion]

Now, in ΔABC and ΔPQR

ABPQ = [ given ]

∠ABC = ∠ [∵ ΔABD ∼ ΔPQM]

⇒ ΔABC ΔPQR [SAS criteion]

13. D is a point on the side BC of a triangle ABC such that ∠ADC = ∠ BAC. Show that CA2 = CB.CD

Solution:

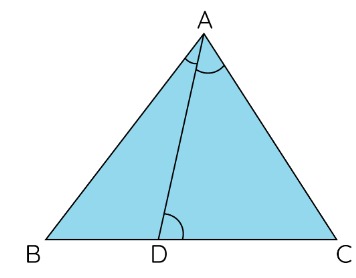
In ΔABC and ΔDAC:

∠BAC = ∠ (Given in the statement)

∠ACB = ∠ ( angles)

⇒ ΔABC ∼ Δ (AA criterion)

If two triangles are similar, then their corresponding sides are

⇒ CACD =

⇒ CA2 = CB ×

Hence, proved.

14. Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ∆ABC ~ ∆ PQR

Solution:

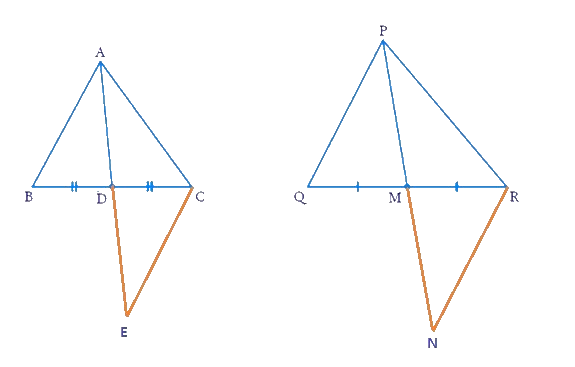
In ΔABD and ΔCDE:

AD = [By Construction]

BD = [AD is the ]

∠ADB = ∠ [ opposite angles]

Therefore, ΔABD ≅ Δ [By SAS criterion of congruence]

⇒ AB = by CPCT ...(i)

Also, in ΔPQM and ΔMNR:

PM = (By Construction)

QM = (PM is the )

∠PMQ = ∠ ( angles)

Therefore, ΔPQM = Δ (By criterion of congruence)

⇒ PQ = (CPCT)...(ii)

Now, ABPQ = ACPR = ADPM (Given)

⇒ = ACPR = ADPM (from (i) and (ii))

⇒ CERN = ACPR =

⇒ CERN= ACPR = (2AD = and 2PM = )

Therefore, ΔACE ~ Δ (By similarity criterion)

Therefore, ∠CAE = ∠

Similarly, ∠BAE = ∠

Hence, ∠CAE + ∠BAE = ∠RPN + ∠

⇒ ∠BAC = ∠

⇒ ∠A = ∠ ....(iii)

Now, In ΔABC and ΔPQR

ABPQ =

∠A = ∠ [from (iii)]

Therefore, ΔABC ~ ΔPQR [By SAS similarity criterion]

15. A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower

Solution:

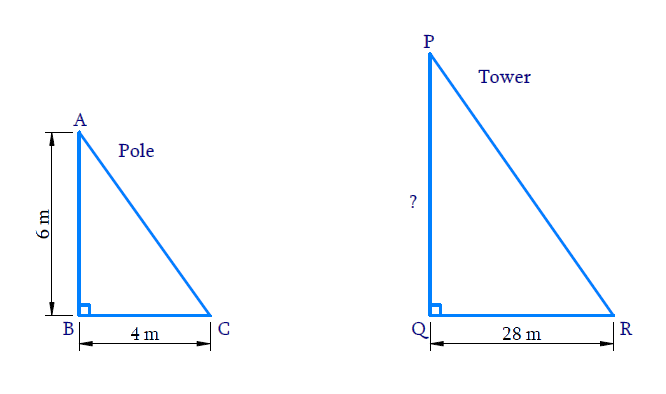
AB is the pole = m

BC is the shadow of pole AB = m

PQ is the tower = ?

QR is the shadow of the tower PQ = m

In ΔABC and ΔPQR

∠ABC = ∠PQR = º (The objects and shadows are to each other)

∠BAC = ∠ (Sunray falls on the pole and tower at angle, at the same time)

⇒ ΔABC ∼ Δ (AA criterion)

The ratio of any two corresponding sides in two equiangular triangles is always the same.

⇒ ABBC =

⇒ 64 = PQ28

⇒ PQ = (6 × 28)4

⇒ PQ = m

Hence, the height of the tower is 42 m.

16. If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that ABPQ = ADPM

Solution:

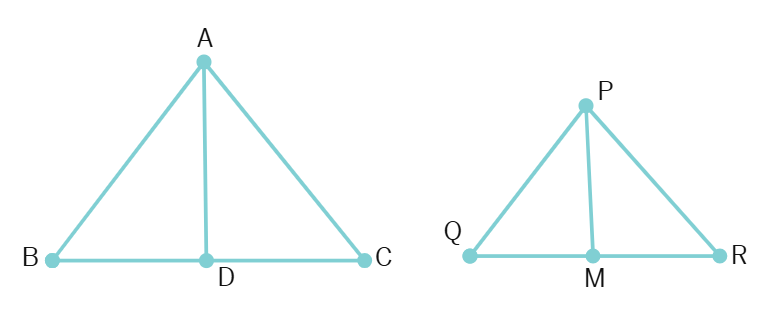
Given, ΔABC ∼ Δ

⇒ ∠ABC = ∠ ( angles) --------- (1)

⇒ ABPQ = ( sides)

⇒ABPQ = (BC/2)(QR/2)

⇒ ABPQ = (D and M are mid-points of and QR) ------------ (2)

In ΔABD and ΔPQM,

∠ABD = ∠ (from 1)

ABPQ = (from 2)

⇒ ΔABD ΔPQM ( criterion)

⇒ ABPQ= = ( sides)

⇒ ABPQ = ADPM

Chapter 6: Triangles

Glossary

Exercise 6.3

(i)

(ii)

(iii)

(iv)

(v)

(vi)

(i)

(ii)

(iii)

(iv)

(i)

(ii)

(i)

(ii)

(iii)

Sign in to Innings2

Chapter 6: Triangles

Reset Progress

Glossary

Exercise 6.3

(i)

(ii)

(iii)

(iv)

(v)

(vi)

(i)

(ii)

(iii)

(iv)

(i)

(ii)

(i)

(ii)

(iii)