Trigonometric Ratios of Some Specific Angles
From geometry, you are already familiar with the construction of angles of 30°, 45°, 60° and 90°. In this section, we will find the values of the trigonometric ratios for these angles and, of course, for 0°.
Look at the triangle to the side
△AFD has an angle ∠DAF of measure 45 o.
It is a right-angled triangle.
If ∠A = 45o then ∠D =
This means that DF =
Let us assume DF = AF = a.
From Pythogoras theorem we have
AD =
sin A = sin 45° =
cos A = cos 45° =
tan A = tan 45° =
Also, cosec 45° =
with sec 45° =
and cot 45° =
Let us now try to find the trigonometric ratios for 60o.
When you hear 60 degress the triangle that comes to mind is
△ABC has an ∠A of 60o.
It is an equilateral triangle. Draw a perpendicular from C to side AB.
∆ACD is
AD = DB =
Since ∆ABC is equilateral, AB = BC = AC.
Since ∆ACD is a
If AC = 2a, then AD =
For ∆ACD, we have AC = 2a and AD = a. We need to find CD. Using pythagoras theorem, we get CD =
Now that we have all the sides:
sin A = sin 60° =
cos A = cos 60° =
tan A = tan 60° =
Further, cosec 60° =
sin ACD = sin 30° =
cos ACD = cos 30° =
tan ACD = tan 30° =
So, we can conclude that: cosec 30° =
What about 90o and 0o? Let's see if we can easily find the trigonometric ratios of these special angles.
When we talk about the sine of an angle, we are referring to the ratio of the length of the side opposite the angle in a right triangle to the length of the hypotenuse of that triangle.
So, if we have a right triangle with one angle equal to 0°, the opposite side of the triangle will have a length of
And, if the opposite side has a length of 0, then the ratio of that side to the hypotenuse will also be
Let's try this out with a simple exercise. Check the triangle to the side. Move the top of the triangle(B) towards C. As you can see, as the angle decreases, the size of BC(height) also decreases.
In this triangle sinA =
But as ∠A becomes 0°, BC also tends towards
And if BC = 0 then
That means sin A = sin 0° =
What happens to cos A? we have: cos A =
Thus, we define : sin 0° = 0 and cos 0° = 1.
Using these, we have :
tan 0° =
We also get: sec 0° =
As in the previous example, move A towards C. We can see that as the ∠A increases towards 90o, AB becomes almost equal to
When ∠A =
Thus, sin 90° =
What about cos 90° ? The side AB is nearly zero, so cos A is very close to
So, we define : sin 90° = 1 and cos 90° = 0.
Using this, we get: tan 90° =
Remark: From the table above you can observe that as ∠A increases from 0° to 90°, sin A increases from 0 to 1 and cos A decreases from 1 to 0.
6. In ∆ ABC, right-angled at B, AB = 5 cm and ∠ACB = 30°. Determine the lengths of the sides BC and AC.
Solution : To find the length of the side BC, we will choose the trigonometric ratio involving BC and the given side AB. Since BC is the side adjacent to angle C and AB is the side opposite to angle C, therefore
i.e.
which gives BC =
To find the length of the side AC, we consider:
sin 30° =
Substituting the values
i.e., AC =
Note that alternatively we could have used Pythagoras theorem to determine the third side in the example above,
i.e., AC =
Example 7
7. In Δ PQR, right-angled at Q, PQ = 3 cm and PR = 6 cm. Determine ∠ QPR and ∠ PRQ.
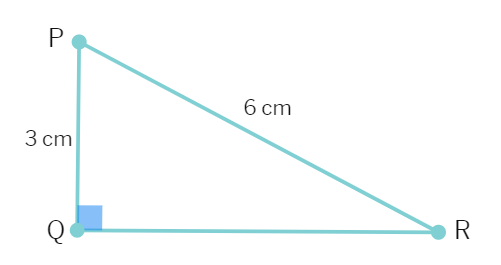
Solution : Given PQ =
Therefore,
So, ∠ PRQ =
and therefore, ∠ QPR =
You may note that if one of the sides and any other part (either an acute angle or any side) of a right triangle is known, the remaining sides and angles of the triangle can be determined.
Example 8
8. If sin (A – B) =
Solution : Since, sin (A – B) =
Also, since cos (A + B) =
Solving (1) and (2), we get : A =
The below table shows the most common angles and their trigonometric ratios.
| ∠A | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| Sin | 0 | 1 | |||
| Cos | 1 | 0 | |||
| Tan | 0 | 1 | Not Defined | ||
| Cosec | Not Defined | 2 | 1 | ||
| Sec | 1 | 2 | Not Defined | ||
| Cot | Not Defined | 1 | 0 |
