Measuring Line Segments
We have learnt in the previous section about line segments. A triangle is made of
We saw that a line segment is a
To compare any two line segments, we need to find a relation between their lengths.
This can be done in several primitive ways.
Comparison by observation
Comparison by observation is a simple and useful method only when the difference in the lengths is very obvious i.e. a large margin of difference.
Using tracing paper, we trace the line segments.
- Comparison by Tracing
Click on the red line segment and click on the copy icon. Now, try to align the two separate segments such that they overlap each other. This same concept is used when trying to measure the lengths of different line segments.
Are the two line segments given below of equal length?
We can see that the accuracy of the method (for measurment of line segments) depends heavily on how well the tracing has been done. Also, we come to an understanding that the method is time-consuming and not very efficient. Thus, we need a better method.
Comparison using Ruler and a Divider
The Universal accepted method for measuring line segments. The ruler also provides us with quantifiable values for the length.
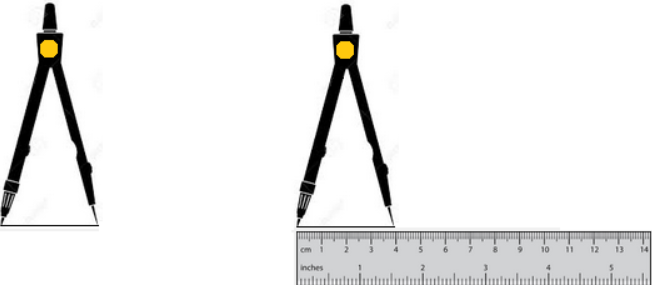
Using a Ruler: A ruler (or a scale) is a simple and direct way to measure the length of a line segment.
Align one end of the segment with the zero mark on the ruler.
Check the measurement where the segment ends.
Measure the second line in the same way.
The segment with a greater numerical value is longer.
Using a Divider: A divider is a more accurate tool for comparing line segments without measuring them numerically. It consists of two pointed arms that can be adjusted to match a length.
Place one end of the divider at one endpoint of the first line segment.
Adjust the other end to reach the second endpoint of the segment.
Transfer this length to the second line segment by placing one point of the divider at its endpoint.
If the second segment is longer, there will be a gap.
If the second segment is shorter, the divider will extend beyond it.
If both match exactly, they are equal in length.
Advantages of a Divider Over a Ruler
More accurate as it directly compares lengths without relying on numerical readings.
No parallax error because no direct scale reading is involved.
Useful for uneven surfaces where rulers may not sit flat.
Have you seen or can you recognise all the instruments in your instrument box? Among other things, you have a ruler and a divider.
Note how the ruler is marked along one of its edges. It is divided into 15 parts. Each of these 15 parts is of length 1cm.
Each centimetre is divided into
Each subpart of the division of a cm is
1 mm is
2 mm is
2.3 cm will mean
In the above drawing panel Place the zero mark of the ruler at A. Read the mark against B. This gives the length of AB.
Suppose the length is 5.8 cm, we may write, Length AB = 5.8 cm or more simply as AB = 5.8 cm.
There is room for errors even in this procedure.
The thickness of the ruler may cause difficulties in reading off the marks on it.
Positioning Error
The angle at which we measure is very important. In order to minimize, especially due to the position of our eye, always view the scale marks from just vertically above(90O angle). Otherwise, angular viewing errors will arise.

