Enhanced Curriculum Support
This is a comprehensive educational resource designed to provide students with the tools and guidance necessary to excel. This support system is structured to cater to various aspects of learning, ensuring that students are well-prepared for academic challenges and practical applications of mathematical concepts. Some are the key benefits are mentioned below:
Comprehensive Learning: This holistic approach helps students gain a thorough understanding of the subject. Practical Application: The resources encourage students to apply mathematical concepts to real-life scenarios, enhancing their practical understanding and problem-solving skills.
Critical Thinking and Reasoning: Value-Based and HOTS questions promote critical thinking and reasoning abilities. These skills are crucial for students to tackle complex problems and make informed decisions.
Exam Preparedness: Sample Question Papers and NCERT Exemplar Solutions provide ample practice for exams. They help students familiarize themselves with the exam format and types of questions, reducing exam anxiety.
Ethical and Moral Development: Value-Based Questions integrate ethical and moral lessons into the learning process, helping in the overall development of students' character and social responsibility. By incorporating these diverse elements, Enhanced Curriculum Support aims to provide a robust and well-rounded knowledge, preparing students for both academic success and real-world challenges.
Sec A
1. A gang of labors promise to do a piece of work in 10 days, but 5 out of them become absent. If the rest of the gang do the work in 12 days, find the original number of men.
(a) 35 (b) 25 (c) 40 (d) 30
2. A mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of base. How many parts of base will be used in mixture by mixing 7 part of red pigment?
(a) 63 (b) 49 (c) 56 (d) 70
3. x and y are in inverse proportion. When x = 12, y = 3. Which of the following is not a possible pair of corresponding values of x and y?
(a) 5 and 6 (b) 10 and 3.6 (c) 4 and 9 (d) 72 and 0.5
4. If 5 workers can complete a task in 12 days, how many days will 10 workers take to complete the same task?
5. If 8 pens cost ₹96, find the cost of 5 pens.
6. Two quantities x and y are in direct proportion. If x=6 when y=18, find y when x=10.
7. If 15 kg of rice costs ₹450, find the cost of 20 kg of rice.
8. A machine fills 500 bottles in 5 hours. How many bottles can it fill in 3 hours?
Sec B
1. The distance between school and house of a girl is given by 5 cm in a picture, using the scale 1cm: 5 km. Find the actual distance between the two places?
2. From the following table, determine if x and y are in direct proportion or not.
| x | y |
|---|---|
| 4 | 24 |
| 7 | 42 |
| 10 | 60 |
| 16 | 96 |
(OR)
A contractor undertook a contract to complete a part of a stadium in 9 months with a team of 560 persons. Later on, it was required to complete the job in 5 months. How many extra persons should he employ to complete the work?
Sec C
1. An electric pole, 14 metres high, casts a shadow of 10 metres. Find the height of a tree that casts a shadow of 15 metres under similar conditions.
2. Suppose 2 kg of sugar contains 9 × 10^6 crystals. How many sugar crystals are there in (i) 5 kg of sugar ? (ii) 1.2 kg of sugar ?
3. If y varies directly with x, write an equation for the direct variation. Then find each value. a. If y = -12 when x = 9, find y when x = -3. b. Find y when x = 10 if y = 8 when x = 20.
4. A car travels 240 km in 4 hours. If the speed remains constant, how far will it travel in 7 hours?
5. If the cost of 12 apples is ₹180, find the cost of 7 apples and 25 apples.
6. A truck consumes 40 liters of fuel to cover 200 km. How much fuel will it consume to cover 350 km?
7. A factory produces 1200 units of a product in 6 days by working 8 hours a day. How many units will it produce in 9 days by working 10 hours a day?
8. A car is traveling at a speed of 72 km/h. How long will it take to cover a distance of 540 km?
Sec D
1. A truck covers a distance of 720 km in 9 hours. How long will it take to cover 480 km at the same speed? If the speed is reduced by 20%, how long will it take to cover 480 km?
2. If 12 men can paint a wall in 18 days, how many men are required to paint the same wall in 9 days? How long will it take for 6 men to paint the same wall?
3. A school has a provision of food for 200 students for 30 days. How long will the food last if 50 more students join the school?
4. The cost of 20 kg of wheat is ₹800. Find the cost of 12 kg and 25 kg of wheat.
5. A pump can fill a tank in 8 hours. If two more similar pumps are added, how long will it take to fill the tank?
Problem 1
During a flood relief campaign, it is observed that 10 volunteers can pack 500 relief kits in 5 hours. If more volunteers join to reduce the time to 3 hours, how many additional volunteers would be needed? Discuss how teamwork and quick action in emergencies can save lives.
Problem 2
A student club needs to complete 600 tasks for an upcoming event. If 5 students working together can complete them in 4 days, how many students would be required to finish in 2 days? How does this scenario illustrate the importance of cooperation and time management in achieving goals?
Q1
A tank can be filled by two different pipes with varying capacities. Pipe X fills the tank in 4 hours, while Pipe Y takes 6 hours. If you want to fill half of the tank, how long should each pipe be used? Would this setup involve direct or inverse proportion?
Q2
In a science experiment, the intensity of light inversely affects the growth rate of a plant. Explain how the growth rate would change if the light intensity is increased threefold. Why does this represent an inverse proportional relationship, and how could you represent it graphically?
Q3
You are given two hoses to fill a swimming pool. Hose A fills it in 10 hours alone, while Hose B fills it in 15 hours alone. You are asked to fill the pool in 5 hours. Can you use both hoses to meet this requirement? If yes, explain how the combined rates create an inverse proportion and calculate the result.
Choose the correct option
Questions
1. Which of the following is in direct proportion?
(a) One side of a cuboid and its volume.
(b) Speed of a vehicle and the distance travelled in a fixed time interval.
(c) Change in weight and height among individuals.
(d) Number of pipes to fill a tank and the time required to fill the same tank.
2. The number of teeth and the age of a person vary:
(a) directly with each other.
(b) inversely with each other.
(c) neither directly nor inversely with each other.
(d) sometimes directly and sometimes inversely with each other.
3. A truck needs 54 litres of diesel for covering a distance of 297 km. The diesel required by the truck to cover a distance of 550 km is:
(a) 100 litres (b) 50 litres (c) 25.16 litres (d) 25 litres
4. Both x and y are in direct proportion, then
(a) in indirect proportion.
(b) in inverse proportion.
(c) neither in direct nor in inverse proportion.
(d) sometimes in direct and sometimes in inverse proportion.
5. If two quantities p and q vary inversely with each other, then:
(a)
(c) p × q remains constant. (d) p – q remains constant.
Fill in the blanks
Questions
1. If x and y are inversely proportional then ? = k where k is positive constant.
2. If 12 pumps can empty a reservoir in 20 hours, then time required by 45 such pumps to empty the same reservoir is ? hours.
3. Side of a rhombus and its perimeter are in ? proportion.
4. On increasing a, b increases in such a manner that
5. The perimeter of a circle and its diameter vary ? with each other.
6. If the thickness of a pile of 12 cardboard sheets is 45 mm, then the thickness of a pile of 240 sheets is ? cm.
7. If the area occupied by 15 postal stamps is 60
State True (or) False
Questions
1. When the speed is kept fixed, time and distance vary inversely with each other.
2. Length of a side of a square and its area vary directly with each other.
3. When two quantities x and y are in inverse proportion, then
4. Length of a side of an equilateral triangle and its perimeter vary inversely with each other.
5. If x and y are in direct proportion, then (x – 1) and (y – 1) are also in direct proportion.
6. If one angle of a triangle is kept fixed then the measure of the remaining two angles vary inversely with each other.
Answer the following questions
Questions
1. In a scout camp, there is food provision for 300 cadets for 42 days. If 50 more persons join the camp, for how many days will the provision last?
2. If two cardboard boxes occupy 500 cubic centimetres space, then how much space is required to keep 200 such boxes?
3. Under the condition that the temperature remains constant, the volume of gas is inversely proportional to its pressure. If the volume of gas is 630 cubic centimetres at a pressure of 360 mm of mercury, then what will be the pressure of the gas if its volume is 720 cubic centimetres at the same temperature?
4. Which of the following vary directly and which vary inversely with each other and which are neither of the two?
(i) The time taken by a train to cover a fixed distance and the speed of the train.
(ii) The distance travelled by CNG bus and the amount of CNG used.
(iii) The number of people working and the time to complete a given work.
(iv) Income tax and the income.
(v) Distance travelled by an auto-rickshaw and time taken.
(vi) Number of students in a hostel and consumption of food.
(vii) Area of the walls of a room and the cost of white washing the walls.
(viii) The number of people working and the quantity of work.
(ix) Simple interest on a given sum and the rate of interest.
(x) Compound interest on a given sum and the sum invested.
(xi) The quantity of rice and its cost.
(xii) The height of a tree and the number of years.
(xiii) Increase in cost and number of shirts that can be purchased if the budget remains the same.
(xiv) Area of land and its cost.
(xv) Sales Tax and the amount of the bill.
5. l varies directly as m and l is equal to 5, when m =
6. Sobi types 108 words in 6 minutes. How many words would she type in half an hour?
7. Find the values of x and y if a and b are in inverse proportion: (a) 12 x 8 (b) 30 5 y
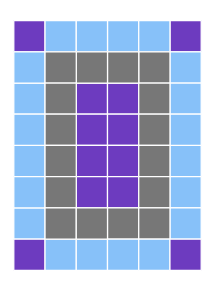
8. Write at least five ratio statements about this quilt, which has white, blue, and purple squares. How many squares of each colour will be there in 12 such quilts?
9. Ravi starts for his school at 8:20 a.m. on his bicycle. If he travels at a speed of 10km/h, then he reaches his school late by 8 minutes but on travelling at 16 km/h he reaches the school 10 minutes early. At what time does the school start?
10. The variable x is inversely proportional to y. If x increases by p%, then by what per cent will y decrease?
Q1
With improving technology, the need for better infrastructure continues to increase. When banks reduce the interest rates (say as a result of reduced REPO rates), we often witness more road and building construction projects getting initiated. The construction costs depend on the cost of material, transport, labour charge, etc. When the number of construction projects increases, the demand for labourers also increases and hence the labour cost increases further.
Do you think the REPO rate can impact the cost of constructing a house/apartment? Mrs. Shenoy is supervising the construction of an apartment. She realised that the construction cost is different for each floor, primarily because of the additional labour involved in carry ing the material to the higher floors.
Mrs. Shenoy collects the charges quoted by different labour groups for different floors. A part of the data is shown in the table. Classify these charges in one of these three categories. Additional cost for each floor is:
1. Directly proportional to the number of floors
2. Inversely proportional
3. Not related
| S.No. | Group | Ground Floor Price (Rs./ | First Floor Price (Rs./ | Second Floor Price (Rs./ |
|---|---|---|---|---|
| 1 | Wall makers | 100 | 130 | 160 |
| 2 | Plastering | 45 | 60 | 75 |
| 3 | Tile workers (floor) | 100 | 100 | 100 |
| 4 | Window/door workers | 700 | 700 | 700 |
| 5 | Painting | 30 | 40 | 50 |
1. Fill the table based on your classification.
| Directly Proportional | Inversely Proportional | Not Related |
|---|---|---|
2. To minimise the cost of the project, Mrs. Shenoy wanted to negotiate and get the lowest quote from the labour groups. However, to save her time, she decided to focus only on those labour groups whose costs were dependent on the number of floors and whose per square foot cost for the ground floor was more than ₹50. Which groups out of those listed in the table would she talk to?
Sol 1
(1)
| Directly Proportional | Inversely Proportional | Not Related |
|---|---|---|
| Wall makers | Tile workers (floor) | |
| Plastering | Window/door workers | |
| Painting |
(2) Therefore, Mrs. Shenoy would talk to Wall makers for negotiation.
Q2
Mr. Vargese was fond of driving. There were times when this hobby would make him spend extra money, especially when he used to drive alone from his hometown, Kannur, to Bengaluru, which is about 300 km away. For a round-trip journey, his cost on petrol alone was about ₹4500, whereas the bus or train would cost him around ₹2000. These are average costs of the round-trip across multiple trips.
Mr. Vargese used to fill 30 litres of petrol each time he refilled the car tank. He had to wait for a long time to get back the change. To solve this problem, he made a habit of filling
petrol for a fixed amount of money. These days, he fills petrol for ₹3000. He continues this habit even now in the age of payment through cards and online payment.
1. Since the traffic and road conditions between Kannur and Bangalore did not change much during this time, Mr. Vargese found that, on an average, the money he spent on fuel was directly proportional to the distance travelled. What is the constant of proportionality?
2. If P is the petrol price, which varies often, then is P directly proportional to the amount of petrol or inversely proportional to the amount of petrol that Mr. Vargese fills in his car every time he goes to a petrol station? Remember that he always fills as much petrol as he gets for ₹3000.
3. Mr. Vargese planned a South India trip with his family in his car. He figured out that he would have travelled at least 4500 km when he finishes the journey. If the fuel price per km is the same as what is applicable to his journey from Kannur to Bengaluru, then which of the following is the correct estimation of the total cost of fuel for his South India trip? Choose the closest answer.
(a) ₹28,000
(b) ₹34,000
(c) ₹45,000
(d) ₹48,000
4. The cost of fuel for his South India trip really made Mr. Vargese rethink about his mode of transport. He decided to look at electric cars. He learnt that the cost of electricity for an electric car is around ₹1.5 /km. He also learnt that he has to plan his trip such that at every major town he needs to halt for some time to charge the battery. To answer if this was worth it, let us answer these two questions: How much money would Mr. Vargese spend during one round-trip on electricity? How much would he save compared to petrol?
Sol 2
(1) Constant of proportionality k is ₹7.5 per km.
(2) P is inversely proportional to the amount of petrol filled.
(3) Option (b)
(4) Mr. Vargese would spend ₹900 on electricity for the round trip and would save ₹3600 compared to petrol.
Q3
A spring balance is a type of weighing scale that consists of a spring fixed at one end and having a hook at the other end to attach the objects to be weighed. It has a scale with equally spaced markings to indicate the weight of the objects being weighed. You can make your own simple spring balance to measure the weights of some lighter objects.


The spring balance shown in Fig. 5.1 is useful in weighing objects, which fall in the weight range of 100 g to 400 g. For objects weighing below 100 g and above 400 g, the spring used here doesn’t give accurate readings. Table 5.3 shows the observations made while testing the spring balance.
| S.No. | Known weight addded | Weight added above 100g | Displacement from 0 g (mm) | Displacement from 100 g mark (mm) |
|---|---|---|---|---|
| 1 | 100 g | 0 g | 0 5 | 0 0 |
| 2 | 200 g | 100 g | 2 0 | 1 5 |
| 3 | 300 g | 200 g | 3 5 | 3 0 |
| 4 | 400 g | 300 g | 5 0 | 4 5 |
1. Which of the following statements is true about the observation given in Table 5.3?
(a) ‘Known weight added’ is directly proportional to ‘Displacement from 0 g mark’
(b) ‘Known weight added’ is directly proportional to ‘Displacement from 100 g mark’
(c) ‘Weight added above 100 g’ is directly proportional to ‘Displacement from 0 g’
(d) ‘Weight added above 100 g’ is directly proportional to ‘Displacement from 100 g mark’
2. (i) If the ‘Weight added above 100 g’ is 150 g, then the ‘Displacement from 100 g mark’ would be close to ?
(a) 10 mm
(b) 18 mm
(c) 22 mm
(d) 28 mm
(ii) While weighing an object with an unknown weight using this spring balance, if you observe a ‘Displacement from 100 g mark’ of 37.5 mm, then the weight of that object is equal to ? .
3. The constant of proportionality between the force applied on a spring and the increase in the length of the spring is known as the spring constant of that spring. In our experiment above, the spring constant can also be expressed as the constant of proportionality between the weight and the displacement because weight is a measure of force due to gravity. Based on your answer to Question 8 (the right pair which is directly proportional), calculate the spring constant in terms of weight/distance (g/mm). (Note: A constant of proportionality is the ratio between two directly proportional quantities)
Sol 3
(1) Option (a)
(2) (i) Option (c)
(ii) The weight of the object is 350 g.
(3) The spring constant is 20 g/mm.
Q4
Bharat, Manoj and Varun, studying in grade 8, are close friends who are in the same class. Except for the last week of every month, they bring boxes for lunch. They have their lunch together from their boxes, sharing the different foods cooked in each of their homes. All three of them had convinced their parents to allow them to have lunch in their school canteen for the last week of every month. For this purpose, each of them receives ₹400 every month.
Usually, they order three thalis (combo meal), which costs ₹80 each. This way, ₹400 lasts for five days for each of them.
1. There was a hike in the price of all the food items in the canteen and each thali now costs ₹100. But three of them continued to receive only ₹400 every month.
(i) Compare the number of days they can eat the canteen thali after the price hike with the number before:
(a) More after the price hike
(b) Less
(c) Same
(ii) Choose the correct option to fill the blank in the statement below:
“If Bharat, Manoj and Varun continue to receive only ₹400, the number of days they can eat canteen thali is ? to the price of the thali”.
(a) Directly proportional
(b) Inversely proportional
(c) Not related
2. Three of them became curious about the cause for such a price hike in the canteen. They tried to find it out by discussing this with others and realised that the recent increase in the fuel price could be the reason. The table shows the fuel price for the last four years and also the price of the thali in their school canteen.
| Year | Petrol price (per litre) | Diesel price (per litre) | LPG price (per kg) | Price of the thali |
|---|---|---|---|---|
| 2019 | ₹73 | ₹65 | ₹50 | ₹60 |
| 2020 | ₹82 | ₹76 | ₹58 | ₹65 |
| 2021 | ₹90 | ₹85 | ₹64 | ₹75 |
| 2022 | ₹100 | ₹96 | ₹70 | ₹80 |
(i) Choose the correct option to fill the blank in the statement made by Bharat:
“According to the data given in Table 5.4, we can conclude that the price of the thali ? when the price of LPG increases.
(a) Increases
(b) Decreases
(c) Remains the same
(ii) Manoj suggested that “Along with the increase in LPG price, increase in the diesel and petrol price also contributes to the increase in the food price because the truck and vans which deliver the goods will also charge more”. Is Manoj right in making the above statement?
(a) Yes
(b) No
3. On a certain day, three of them ordered 2 pizzas in the school canteen, just for a change. Each pizza has three slices. While they were about to receive their order, their common friend Sachin joined them.
(i) If four of them shared the pizza equally, then the quantity of pizza eaten by each of them is ?
(a) 1 slice
(b) 1.5 slices
(c) 2 slices
(ii) If Riya and Mary also join their table and share the pizzas equally, then the number of slices available to each of them is ?
(a) 0.5
(b) 1
(c) 1.5
(d) 2
(iii) In the above scenario of sharing the pizza, the quantity of pizza received by each person is ? to the number of people around the table.
(a) Directly Proportional
(b) Inversely Proportional
(c) Not Related
4. On some other day, Bharat, Manoj and Varun were having lunch from their boxes. Each of them had brought different food items. This time, again, they are joined by Sachin, Riya and Mary, who also brought their boxes with another three different food items in their boxes. If all six of them shared each other’s food, then the number of food items tasted by each of them is ? to the number of people in the group.
(a) Directly Proportional
(b) Inversely Proportional
(c) Not Related
Sol 4
(1) (i) Option (b)
(ii) Option (b)
(2) (i) Option (a)
(ii) Option (a)
(3) (i) Option (b)
(ii) Option (b)
(iii) Option (b)
(4) Option (a)
