Enhanced Curriculum Support

SecA

1. The total number of propositions in the Euclid’s Elements is:

(a) 460 (b) 465

(c) 32 (d) 13

2. The number of dimensions, a surface has:

(a) 2 (b) 1

(c) 0 (d) 3

3. The edges of a surface are:

(a) Curves (b) None of these

(c) Point (d) Lines

4. Euclid stated that if equals are added to equals, the wholes are equal in the form of:

(a) A definition (b) An axiom

(c) A theorem (d) None of these

5. The number of dimensions a line has.

(a) 1 (b) 2 (c) 0 (d) 3

6. State Euclid’s fifth postulate.

7. How is a ray different from a line in Euclid’s geometry?

SecB

1. In how many lines two distinct planes can intersect ?

2. Which of the following statements are true and which are false? Give reasons for your answers.

(i) Two lines can intersect at more than one point.

(ii) Two distinct planes can intersect in more than one line.

(iii) If two triangles have the same area, then they are congruent.

(iv) If two angles are equal, their supplements are also equal.

3. State and explain Euclid’s first two postulates with examples.

4. Explain how the statement "The whole is greater than the part" can be applied to solve geometrical problems.

5. Prove that the diagonals of a rectangle bisect each other using Euclid’s axioms.

SecC

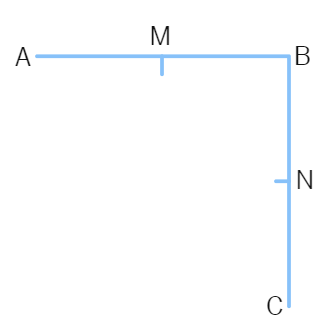
1. (i) AB = BC, M is the mid-point of AB and N is the mid-point of BC. Show that AM = NC.

(ii) BM = BN, M is the mid-point of AB and N is the mid-point of BC. Show that AB = BC.

2. Consider the following postulates.

(i) Given two distinct points, there is a unique line that passes through them.

(ii) A circle can be drawn with any center and radius. Do these postulates contain undefined terms? Are they consistent with Euclid’s geometry?

3. Prove that the sum of two sides of a triangle is always greater than the third side using Euclid’s axioms.

4. Using Euclid’s definitions and axioms, prove that "Two angles of a triangle are together less than two right angles."

5. If a point C lies between A and B such that AC = BC, prove that AC = 1/2 AB. Also, explain the concept of the midpoint.

6. Why is Euclid’s Axiom 5 considered a universal truth? Explain with examples.

Sec D

1. Two postulates are given.

(i) Any two points are connected by exactly one straight line.

(ii) There exist at least three points that are not collinear.

Discuss whether these postulates are consistent with each other and with Euclid's postulates. Provide detailed reasoning and examples.

2. Prove that "Two distinct lines cannot intersect at more than one point" using Euclid’s axioms and postulates. Then, extend the proof to show that two planes can intersect in exactly one line.

Problem 1

1. In a construction project, a team is responsible for laying the foundation of a building. The team leader insists on using accurate measurements and adhering strictly to geometric principles, particularly ensuring that the angles and lengths conform to the design specifications.

Discuss how the principles of Euclid’s geometry, such as the exactness of measurements and the consistency of geometric constructions, reflect the values of integrity and fairness in real-life situations. Why is it important for professionals, like engineers and architects, to uphold these values? How can disregarding these principles lead to larger ethical issues?

Problem 2

Euclid’s dedication to discovering and organizing geometric truths exemplifies a lifelong commitment to learning and intellectual honesty. His work reminds us of the importance of seeking truth in all areas of life.

In what ways can the pursuit of truth, as demonstrated in Euclid’s geometric investigations, inspire you in your own education and personal growth? How does valuing truth and knowledge contribute to a more ethical and informed society? Provide an example where seeking the truth had a positive impact on your life or the lives of others.

Q1

Euclid’s fifth postulate states: "If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the angles are less than two right angles."

Consider a scenario where two straight lines, when extended, appear to remain parallel. If these lines meet at some extremely distant point, what might this imply about the nature of the angles formed by a transversal cutting these lines? Can this situation arise in a non-Euclidean geometry? How does Euclid's fifth postulate change in such a geometry?

Q2

Euclid’s geometry is largely based on the notion of flat, two-dimensional space. Consider how Euclidean concepts might be generalized to three dimensions or even higher dimensions.

Choose one of Euclid’s postulates (other than the fifth) and generalize it to three dimensions. For instance, how would Euclid’s first postulate (a straight line can be drawn from any point to any point) be expressed in three-dimensional space? Discuss any new complexities that arise when moving from two to three dimensions, particularly in the context of defining and understanding geometric objects.

Q3

A surveyor needs to determine the distance between two points, A and B, located on opposite banks of a river, without directly measuring across the river. The surveyor constructs a right-angled triangle on one bank, with one leg along the bank and the other leg perpendicular to the river.

Using Euclid’s axioms, explain how the surveyor can indirectly calculate the distance between points A and B. Consider the implications of Euclid's first postulate (a straight line can be drawn from any point to any point) and the use of similar triangles in your explanation.

Questions

1. Euclid’s second axiom is:

(A) The things which are equal to the same thing are equal to one another.

(B) If equals be added to equals, the wholes are equal.

(C) If equals be subtracted from equals, the remainders are equals.

(D) Things which coincide with one another are equal to one another.

2. Euclid’s fifth postulate is:

(A) The whole is greater than the part.

(B) A circle may be described with any centre and any radius.

(C) All right angles are equal to one another.

(D) If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.

3. The things which are double of the same thing are:

(A) equal

(B) unequal

(C) halves of the same thing

(D) double of the same thing

4. Axioms are assumed:

(A) universal truths in all branches of mathematics

(B) universal truths specific to geometry

(C) theorems

(D) definitions

5. John is of the same age as Mohan. Ram is also of the same age as Mohan. State the Euclid’s axiom that illustrates the relative ages of John and Ram:

(A) First Axiom (B) Second Axiom

(C) Third Axiom (D) Fourth Axiom

6. If a straight line falling on two straight lines makes the interior angles on the same side of it, whose sum is 120°, then the two straight lines, if produced indefinitely, meet on the side on which the sum of angles is:

(A) less than 120° (B) greater than 120°

(C) is equal to 120° (D) greater than 180°

State if the given statements are True (or) False

7. Write whether the following statements are True or False? Justify your answer :

8. Euclidean geometry is valid only for curved surfaces.

9. The boundaries of the solids are curves.

10. The edges of a surface are curves.

11. The things which are double of the same thing are equal to one another.

12. If a quantity B is a part of another quantity A, then A can be written as the sum of B and some third quantity C.

13. The statements that are proved are called axioms.

14. “For every line l and for every point P not lying on a given line l, there exists a unique line m passing through P and parallel to l ” is known as Playfair’s axiom.

15. Two distinct intersecting lines cannot be parallel to the same line.

16. Attempts to prove Euclid’s fifth postulate using the other postulates and axioms led to the discovery of several other geometries.

17. Write whether the following statements are True or False? Justify your answer.

(i) Pyramid is a solid figure, the base of which is a triangle or square or some other polygon and its side faces are equilateral triangles that converges to a point at the top.

(ii) In Vedic period, squares and circular shaped altars were used for household rituals, while altars whose shapes were combination of rectangles, triangles and trapeziums were used for public worship.

(iii) In geometry, we take a point, a line and a plane as undefined terms.

(iv) If the area of a triangle equals the area of a rectangle and the area of the rectangle equals that of a square, then the area of the triangle also equals the area of the square.

(v) Euclid’s fourth axiom says that everything equals itself.

(vi) The Euclidean geometry is valid only for figures in the plane.

18. Ram and Ravi have the same weight. If they each gain weight by 2 kg, how will their new weights be compared ?

19. Solve the equation a – 15 = 25 and state which axiom do you use here.

20. Read the following statement:

“A square is a polygon made up of four line segments, out of which, length of three line segments are equal to the length of fourth one and all its angles are right angles”.

Define the terms used in this definition which you feel necessary. Are there any undefined terms in this? Can you justify that all angles and sides of a square are equal?

21. Read the following statements which are taken as axioms :

(i) If a transversal intersects two parallel lines, then corresponding angles are not necessarily equal.

(ii) If a transversal intersect two parallel lines, then alternate interior angles are equal.

Is this system of axioms consistent? Justify your answer.

Q1

A construction team is working on a triangular plot of land. The sides of the triangle are given as 7 m, 8 m, and 9 m. The team is tasked with verifying whether they can construct a triangle using these measurements. They need to use Euclid’s postulates and axioms to justify the construction.

(a) According to Euclid's first postulate, what can be said about the possibility of constructing a triangle with sides 7 m, 8 m, and 9 m?

(b) Which Euclidean axiom can be used to verify if the sum of any two sides of this triangle is greater than the third side?

(c) Using Euclid’s axioms, how would you explain the uniqueness of the triangle that can be constructed with these side lengths?

(d) If a perpendicular is drawn from one vertex of the triangle to the opposite side, explain how Euclid’s postulates ensure the existence and uniqueness of this perpendicular.

Sol 1

(a)

Euclid's first postulate states that a straight line can be drawn between any two points. Applying this to a triangle, it means we can connect the endpoints of three line segments to form a triangle.

For the given measurements (7 m, 8 m, and 9 m), the triangle inequality theorem must also hold: 7 + 8 > 9 (True)
7 + 9 > 8 (True)
8 + 9 > 7 (True)

Since these conditions are satisfied, a triangle can indeed be constructed with these side lengths, in accordance with Euclid’s first postulate.

(b)

The Euclidean axiom used is: "The whole is greater than the part."

In the context of triangles, this axiom ensures that the sum of any two sides (parts) of the triangle is greater than the third side (the whole side left). This axiom is fundamental to the triangle inequality theorem.

(c)

The uniqueness of the triangle follows from Euclid's fourth postulate: "All right angles are equal to one another."

Additionally, the side-side-side (SSS) congruence criterion in Euclidean geometry states that if the three sides of a triangle are given, only one unique triangle can be constructed. This is because the specific lengths determine fixed angles and shape, ensuring no other triangle can share the exact same side lengths.

(d)

• Existence: Euclid's postulates state that a straight line can be drawn between any two points and that a circle can be drawn with any center and radius. Using these, a perpendicular line can be constructed by determining the shortest distance from the vertex to the opposite side. This ensures that the perpendicular always exists.

• Uniqueness: Euclid's fifth postulate ensures that through a point not on a given line, exactly one perpendicular can be drawn to the line. This guarantees that the perpendicular from the vertex to the opposite side is unique.

Thus, Euclid’s postulates and axioms collectively establish both the existence and uniqueness of the perpendicular.

Q2

In a city planning project, two streets are to be laid out such that they are parallel to each other. The surveyor claims that if two lines are intersected by a transversal, and the corresponding angles are equal, then the lines are parallel.

(a) Which of Euclid’s postulates or axioms justifies the surveyor’s claim about the parallel lines?

(b) If the streets are not exactly parallel and deviate slightly, how would this impact the corresponding angles formed by the transversal? Use Euclid's geometry to explain.

(c) Describe how Euclid’s fifth postulate (also known as the parallel postulate) applies to the layout of these streets.

(d) If an alternate interior angle is found to be unequal, what conclusion can be drawn about the lines, and how does this relate to Euclid's axioms?

Sol 2

(a)

The surveyor's claim is justified by Euclid's axiom:

This axiom is a direct application of the properties of parallel lines in Euclidean geometry. Equal corresponding angles imply that the lines do not meet, no matter how far they are extended.

(b)

If the streets are not perfectly parallel and deviate slightly, the corresponding angles formed by the transversal would no longer be equal.

In Euclidean geometry:

• The measure of corresponding angles reflects the degree of deviation from parallelism.
• A small deviation would result in corresponding angles that are nearly, but not exactly, equal.

Thus, the inequality of corresponding angles indicates that the streets are not truly parallel.

(c)

Euclid’s fifth postulate states:

For parallel streets:

• The sum of the interior angles on the same side of the transversal must equal exactly two right angles.
• This condition ensures that the streets will never meet, maintaining their parallel nature.

(d)

If an alternate interior angle is found to be unequal, it indicates that the two lines are not parallel.

This conclusion is based on Euclid's axiom:

The inequality of alternate interior angles violates this axiom, confirming that the lines deviate and will eventually intersect if extended far enough.