Enhanced Curriculum Support

Sec A

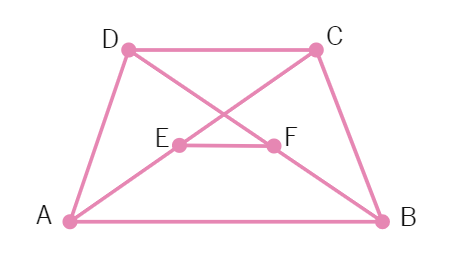
1. In a trapezium ABCD, E and F be the midpoints of the diagonals AC and BD respectively. Then, EF = ?

(a) 12 AB (c) 12 (AB−CD) (b) 12 (AB + CD) (d) 12 CD

2. ABCD is a parallelogram. If is produced to E such that ED bisects BC at O. Then which of the following is correct?

(a) OC = BE (c) AB = OE (b) OE = OC (d) AB = BE

3. A diagonal of a Rectangle is inclined to one side of the rectangle at an angle of 25°. The Acute Angle between the diagonals is :

(a) 115° (b) 40° (c) 50° (d) 25°

4. Two adjacent angles of a parallelogram are in the ratio 4 : 5. The angles are:

(a) 90°,90° (c) 60°,120° (b) 80°,100° (d) 40°,140°

5. Assertion (A): In ABC, E and F are the midpoints of AC and AB respectively. The altitude AP at BC intersects FE at Q. Then, AQ = QP.

Reason (R): Q is the midpoint of AP.

(a) Both A and R are true and R is the correct explanation of A.

(b) Both A and R are true but R is not the correct explanation of A.

(c) A is true but R is false

(d) A is false but R is true.

Sec B

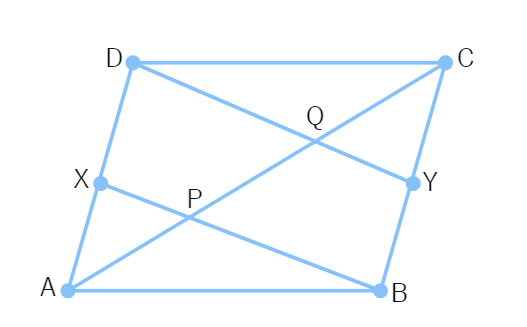
1. In the fig., X and Y are respectively the mid-points of the opposite sides AD and BC of a parallelogram ABCD. Also, BX and DY intersect AC at P and Q, respectively. Show that AP = PQ = QC.

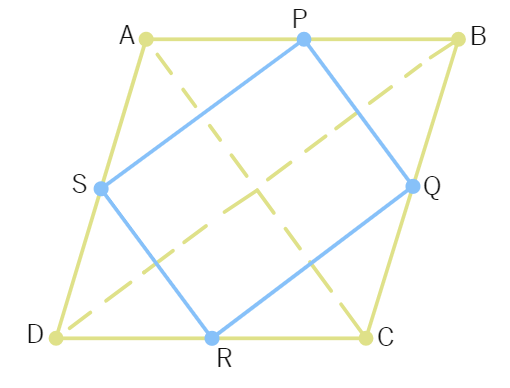
2. Show that the quadrilateral formed by joining the mid-points the sides of a rhombus, taken in order, form a rectangle.

OR

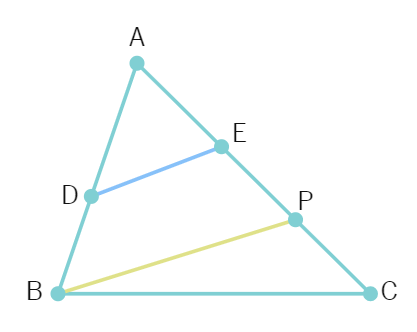
In figure D is mid-points of AB. P is on AC such that PC = 12 AP and DE ∥ BP, then show that AE = 13 AC.

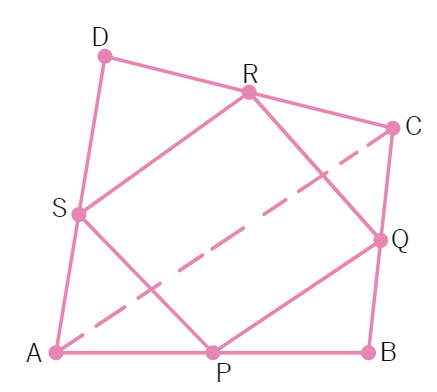
3. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that (i) SR || AC and SR = AC (ii) PQ = SR (iii) PQRS is a parallelogram.

4. ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that:

(i) D is the mid-point of AC

(ii) MD ⊥ AC

(iii) CM = MA = 12 AB

Sec C

1. Read the following text carefully and answer the questions that follow: Modern curricula include several problem-solving strategies. Teachers model the process, and students work independently to copy it. Sheela Maths teacher of class 9th wants to explain the properties of parallelograms in a creative way, so she gave students colored paper in the shape of a quadrilateral and then ask the students to make a parallelogram from it by using paper folding.

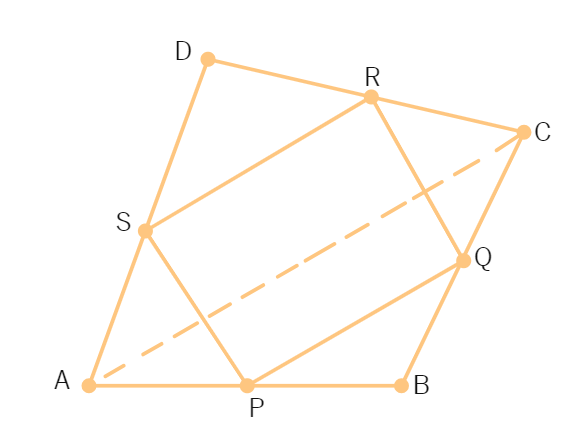
(i) How can a parallelogram be formed by using paper folding?

(ii) If ∠ RSP = 30°, then find RQP.

(iii) If ∠ RSP = 50° , then find SPQ ?

(OR)

If SP = 3 cm, Find RQ.

2. Haresh and Deep were trying to prove a theorem. For this they did the following:

(i) Draw a triangle ABC

(ii) D and E are found as the mid points of AB and AC

(iii) DE was joined and DE was extended to F so DE = EF

(iv) FC was joined.

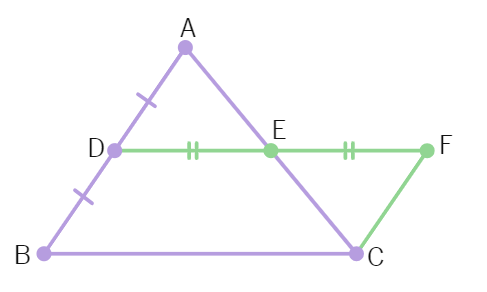
(a) △ADE and △EFC are congruent by which criteria?

(b) Show that CF ∥ AB.

(c) Show that CF = BD.

3. Prove that the line joining the mid-points of the diagonals of a trapezium is parallel to each of the parallel sides and is equal to half of the difference of these sides.

Sec D

1. In a trapezium ABCD, AB ∥ CD. Prove that the line joining the midpoints of the diagonals is parallel to the parallel sides and is equal to half the difference between the lengths of the parallel sides. Explain how this concept applies in dividing a trapezium into two regions of equal area.

2. In a quadrilateral ABCD, it is given that diagonals AC and BD bisect each other at O. Prove that ABCD is a parallelogram. If the lengths of AC and BD are 12 cm and 16 cm respectively, find the lengths of AO, BO, CO, and DO.

3. Prove that the diagonals of a rhombus bisect each other at right angles. Using this property, find the area of a rhombus with diagonals measuring 16 cm and 12 cm.

4. In a kite ABCD, prove that one of its diagonals is the perpendicular bisector of the other. If the diagonals are 10 cm and 24 cm, calculate the area of the kite.

Problem 1

A farmer owns a plot of land in the shape of a trapezium. He plans to divide this land between his two children. He ensures that the division is done using the median, so each child gets an equal share.

How does the concept of the median in a trapezium, which divides it into two equal areas, demonstrate the value of justice and responsibility?

Why is it important to take responsibility for fair decision-making, especially in matters of inheritance or distribution of property?

Problem 2

A surveyor is measuring the sides of a rhombus to verify that the diagonals are perpendicular to each other and bisect each other at right angles. Accurate measurements are essential for ensuring that the rhombus shape is maintained.

How does ensuring that the diagonals of a rhombus bisect each other perpendicularly reflect the value of accuracy and precision?

Why is precision important not only in mathematics but also in daily life when making decisions or performing tasks?

Problem 3

A city government plans to distribute a quadrilateral-shaped piece of land to two families. The land is a parallelogram with diagonals that bisect each other. The government decides to divide the land equally using the diagonals.

How does the concept of diagonals bisecting each other in a parallelogram demonstrate fairness in distributing the land equally?

Can you relate this to the value of equality in real life? Why is it important to ensure fairness when distributing resources?

Q1

In a quadrilateral ABCD, diagonals AC and BD bisect each other at right angles. However, AB ≠ CD and AD ≠ BC.

What type of quadrilateral can ABCD be, and how would you prove it? Explain why the given conditions make it impossible for ABCD to be a parallelogram, square, or rectangle.

Q2

In an isosceles trapezium ABCD, where AB || CD, the diagonals are equal in length. If AB = 8 cm and CD = 12 cm, can you determine the height of the trapezium if one of the diagonals is 10 cm long?

Use the properties of isosceles trapeziums and the Pythagorean theorem to calculate the height. Analyze how the equality of diagonals helps simplify the solution.

Q3

In quadrilateral ABCD, it is known that angle A + angle C = 180°. The diagonals intersect at point O.

Prove that ABCD must be a cyclic quadrilateral. How does the given angle condition help in proving this, and what other properties of cyclic quadrilaterals can you use to support your proof?

Questions

1. Diagonals of a parallelogram ABCD intersect at O. If ∠BOC = 90º and ∠BDC = 50º, then ∠OAB is:

(A) 90º (B) 50º (C) 40º (D) 10º

2. A diagonal of a rectangle is inclined to one side of the rectangle at 25º. The acute angle between the diagonals is:

(A) 55º (B) 50º (C) 40º (D) 25º

3. ABCD is a rhombus such that ∠ACB = 40º. Then ∠ADB is:

(A) 40º (B) 45º (C) 50º (D) 60º

4. The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if:

(A) PQRS is a rectangle

(B) PQRS is a parallelogram

(C) diagonals of PQRS are perpendicular

(D) diagonals of PQRS are equal.

5. The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rhombus, if:

(A) PQRS is a rhombus

(B) PQRS is a parallelogram

(C) diagonals of PQRS are perpendicular

(D) diagonals of PQRS are equal.

6. If bisectors of ∠A and ∠B of a quadrilateral ABCD intersect each other at P, of ∠B and ∠C at Q, of ∠C and ∠D at R and of ∠D and ∠A at S, then PQRS is a:

(A) rectangle (B) rhombus (C) parallelogram

(D) quadrilateral whose opposite angles are supplementary

7. If APB and CQD are two parallel lines, then the bisectors of the angles APQ, BPQ, CQP and PQD form:

(A) a square (B) a rhombus

(C) a rectangle (D) any other parallelogram

8. The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only if:

(A) ABCD is a rhombus

(B) diagonals of ABCD are equal

(C) diagonals of ABCD are equal and perpendicular

(D) diagonals of ABCD are perpendicular.

9. D and E are the mid-points of the sides AB and AC respectively of ∆ABC. DE is produced to F. To prove that CF is equal and parallel to DA, we need an additional information which is:

(A) ∠DAE = ∠EFC

(B) AE = EF

(C) DE = EF

(D) ∠ADE = ∠ECF.

Questions

1. Diagonals AC and BD of a quadrilateral ABCD intersect each other at O such that OA : OC = 3: 2. Is ABCD a parallelogram? Why or why not?

2. Diagonals of a parallelogram are perpendicular to each other. Is this statement true? Give reason for your answer.

3. In quadrilateral ABCD, ∠A + ∠D = 180º. What special name can be given to this quadrilateral?

4. In ∆ABC, AB = 5 cm, BC = 8 cm and CA = 7 cm. If D and E are respectively the mid-points of AB and BC, determine the length of DE.

5. ABCD is a rhombus in which altitude from D to side AB bisects AB. Find the angles of the rhombus.

6. E and F are points on diagonal AC of a parallelogram ABCD such that AE = CF. Show that BFDE is a parallelogram.

7. ABCD is a trapezium in which AB || DC and ∠A = ∠B = 45º. Find angles C and D of the trapezium.

8. P is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.

9. E and F are respectively the mid-points of the non-parallel sides AD and BC of a trapezium ABCD. Prove that EF || AB and EF = 12 (AB + CD).

[Hint: Join BE and produce it to meet CD produced at G.]

10. E is the mid-point of a median AD of ∆ABC and BE is produced to meet AC at F. Show that AF = 13 AC.

11. P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.

12. In a parallelogram ABCD, AB = 10 cm and AD = 6 cm. The bisector of ∠A meets DC in E. AE and BC produced meet at F. Find the length of CF.

13. In the below figure, it is given that BDEF and FDCE are parallelograms. Can you say that BD = CD? Why or why not?

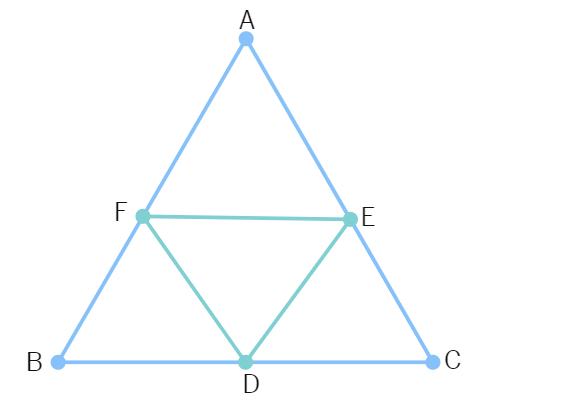
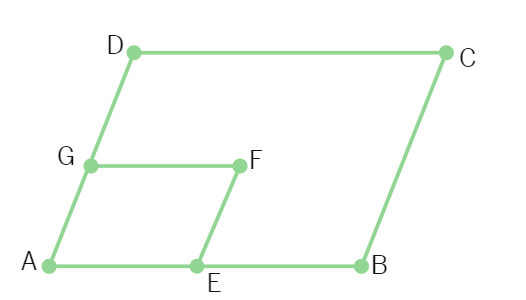
14. In the below figure, ABCD and AEFG are two parallelograms. If ∠C = 55º, determine ∠F.

15. In the below figure, X and Y are respectively the mid-points of the opposite sides AD and BC of a parallelogram ABCD. Also, BX and DY intersect AC at P and Q, respectively. Show that AP = PQ = QC.

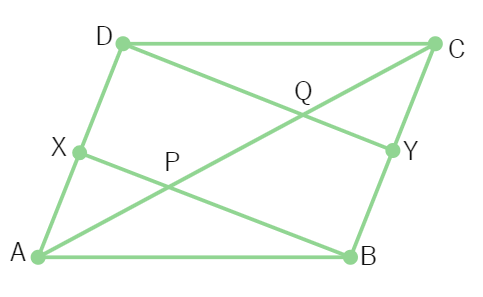
16. In the figure, AX and CY are respectively the bisectors of the opposite angles A and C of a parallelogram ABCD. Show that AX || CY.

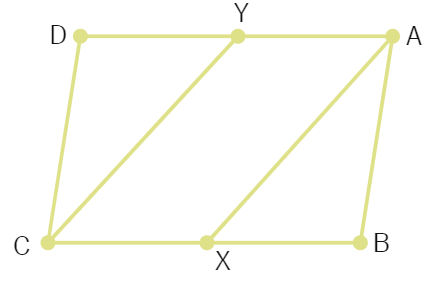
17. Through A, B and C, lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a ∆ ABC as shown in the below figure. Show that BC = 12 QR.

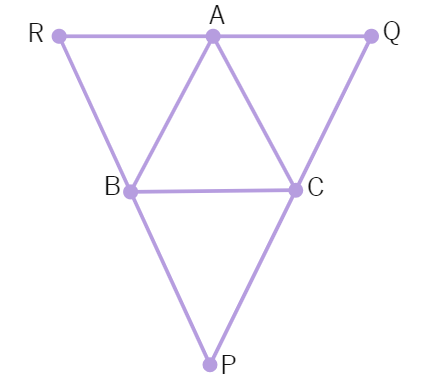
18. Points P and Q have been taken on opposite sides AB and CD, respectively of a parallelogram ABCD such that AP = CQ (see figure). Show that AC and PQ bisect each other.

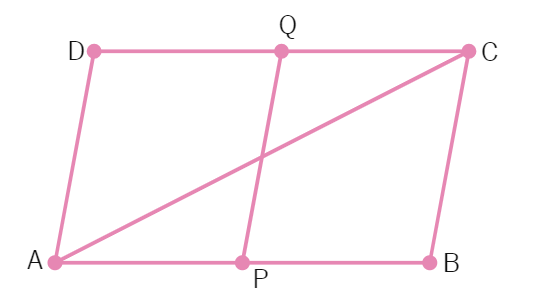
19. In the figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP = ∠DAP. Prove that AD = 2CD.

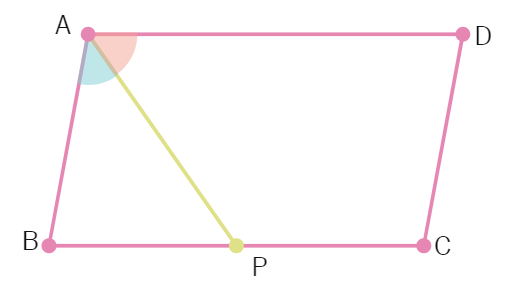
20. PQ and RS are two equal and parallel line-segments. Any point M not lying on PQ or RS is joined to Q and S and lines through P parallel to QM and through R parallel to SM meet at N. Prove that line segments MN and PQ are equal and parallel to each other.

21. Show that the quadrilateral formed by joining the mid-points the sides of a rhombus, taken in order, form a rectangle.

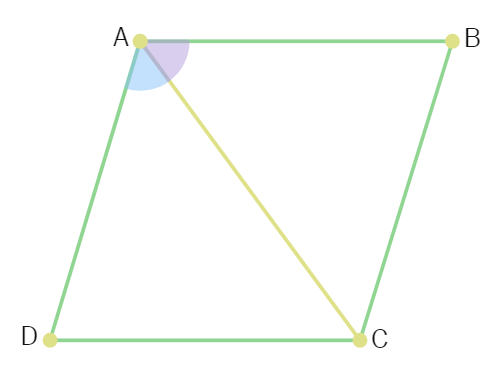
22. A diagonal of a parallelogram bisects one of its angle. Prove that it will bisect its opposite angle also.

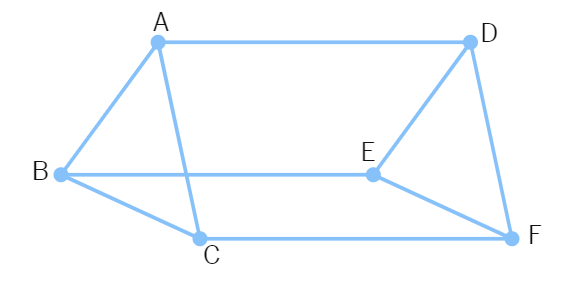
32. In the figure, AB || DE, AB = DE, AC || DF and AC = DF. Prove that BC || EF and BC = EF.

Q1

Faisal Ali is a perfume manufacturer. He farms various kinds of flowers to make perfumes. He has a piece of land on which he wants to farm jasmine and rose shrubs, each occupying equal area. As the farmland lies between two parallel roads, its shape could be approximated to a parallelogram (ABCD), as shown in Fig. 4.2. Mr. Ali thought of two methods for dividing the farmland equally, i.e. to draw a boundary line either along BD or AC.

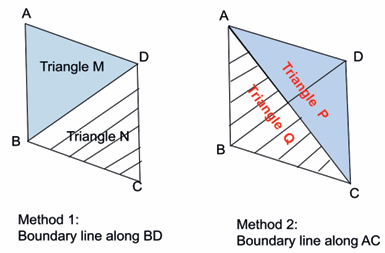
1. If Mr. Ali chooses the blue shaded area for planting jasmine shrubs, how much area is left for planting the rose shrubs?

(a) Less than the blue shaded area

(b) More than the blue shaded area

(c) Both are equal in area

2. Mr. Ali wants to fence the two parts separately. Which method of partitioning will result in more expense for him?

(a) Method 1 by having the boundary line along BD

(b) Method 2 by having the boundary line along AC

(c) Both are the same

Sol 1

1. Mr. Ali is dividing a parallelogram into two triangles either along the diagonal BD or AC. In both cases, the parallelogram is divided into two triangles that have equal areas because a diagonal of a parallelogram divides it into two congruent triangles. Thus, if the blue shaded area is used for planting jasmine shrubs, the remaining area for rose shrubs will be equal to the blue shaded area.

So, the correct answer is: (c) Both are equal in area.

2. The expense for fencing will depend on the length of the boundary line, which is the diagonal in each case. In a parallelogram, the diagonals BD and AC are generally of different lengths unless the parallelogram is a rhombus or square. The longer diagonal will result in more fencing cost. So, if AC is longer than BD, Mr. Ali will incur more expense if he partitions along AC. If BD is longer, the expense will be higher for partitioning along BD.

Since, from the figure, AC> BD, we will have more expense, when fencing the boundary along AC. Thus, (b) Method 2 by having the boundary line along AC.

Q2

1. Mrs. Radha had a rectangular patch of land in her farmhouse to be used as a lawn. She also wants a part of the land to be used for planting trees and have sitting areas. She tells her workers to mark the midpoints of each side of the rectangular patch and use the area obtained by joining the midpoints for creating the lawn. At two opposite corners of the rectangular patch, she decides to have sitting areas with big shady trees. And at the other two opposite corners, she decided to have ornamental plants. The workers fixed small poles to mark out the midpoints of the rectangular patch. They joined the consecutive midpoints with multicoloured pebbles to fix the boundary of the lawn and sow grass seeds in that area.

Assuming the grass growth is uniform throughout, after a few months, what shape does the grass lawn look like?

(a) Rectangle

(b) Square

(c) Rhombus

(d) Trapezium

2. Also, there is a rectangular patch of land unutilised in the backyard. Mrs. Radha decides to use the patch as a vegetable garden, but her daughter insists on growing some herbs too. Which partitioning described below does not satisfy the criterion of equal area allocation for both the purposes?

(a) Partition the land by the imaginary line connecting the midpoint of the longer sides.

(b) Partition the land by the imaginary line connecting the midpoint of the shorter sides.

(c) Partition the land by the imaginary line connecting one pair of opposite vertices.

(d) Partition the land by the imaginary line connecting the midpoint of adjacent sides.

Sol 2

1. Mrs. Radha asks the workers to mark the midpoints of each side of the rectangular patch and join the consecutive midpoints. The figure formed by joining the midpoints of a rectangle is a rhombus.

So, the shape of the grass lawn will look like a rhombus. (c) Rhombus

2. Mrs. Radha wants to partition the rectangular patch of land for equal area allocation for growing vegetables and herbs. The partition should divide the rectangle into two equal areas.

Partitioning by the imaginary line connecting the midpoints of the longer sides divides the rectangle into two equal parts.

Partitioning by the imaginary line connecting the midpoints of the shorter sides also divides the rectangle into two equal parts.

Partitioning by the imaginary line connecting one pair of opposite vertices also divides the rectangle into two equal parts.

However, partitioning by the imaginary line connecting the midpoints of adjacent sides does not divide the rectangle into two equal parts. This partitioning would create two triangles of different areas.

So, the partitioning that does not satisfy equal area allocation is:

(d) Partition the land by the imaginary line connecting the midpoint of adjacent sides.

Q3

Shubhajit is exploring parallelograms and their area. In order to get a better feel for the area occupied by any polygon, Shubhajit usually draws them on a sheet of paper, cuts them out, wraps/covers them over different objects etc. He does this instead of just memorising the formula.

As a further step of his exploration of parallelograms, he decided to fold the parallelograms along a diagonal and also cut it along that. He drew parallelogram ABCD on a sheet of paper for this purpose (Fig. 4.3).

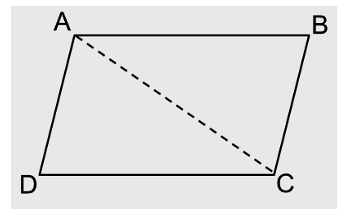
1. Which of the following is true about ∆ABC and ∆ADC? Choose all that apply.

(a) They are congruent to each other.

(b) Both of them have a common hypotenuse, which is AC.

(c) They lie between the same parallels and have equal base lengths.

(d) The area of each of them is half of the area of the parallelogram ABCD.

2. Shubhajit folds the parallelogram ABCD along AC.

(i) Will the the triangles ABC and ADC overlap exactly on each other?

(ii) Which of the following quadrilaterals will result in complete overlap of the triangles when folded along the diagonals? Choose all that apply.

(a) Square

(b) Rectangle

(c) Rhombus

(d) Trapezium

Shubhajit cuts the parallelogram along AC and obtains two triangular pieces, T1 and T2. He wants to completely cover T2 with T1. Among the different steps given below, choose the ones which will be useful to Shubhajit and arrange them in the correct order.

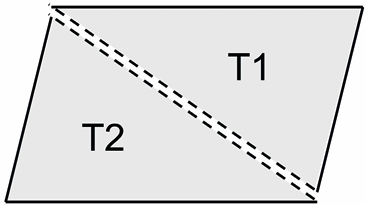
Note: While answering this question, assume the distance between the longer sides of the parallelogram to be H1 and the distance between the shorter sides to be H2. Also, in the answer options, the words ‘left’, ‘right’, ‘top’, ‘bottom’ etc. stand for the respective sides of the paper.

I. Move T1 rightwards by a distance of H1

II. Rotate T1 by 90°, clockwise, about the top-right corner of the parallelogram

III. Move T1 downwards by a distance of H1

IV. Rotate T1 by 180°, clockwise/anti-clockwise, about the top-left corner of the parallelogram

V. Move T1 downward by a distance of H2

VI. Rotate T1 by 270° clockwise about the bottom-left corner of the parallelogram

VII. Move T1 upwards by a distance of H2

VIII. Move T1 leftwards by a distance of H1

Sol 3

1. Which of the following is true about ∆ABC and ∆ADC? These triangles are formed by cutting the parallelogram ABCD along the diagonal AC.

(a) They are congruent to each other.

Yes, the triangles ∆ABC and ∆ADC are congruent because they share the same side (AC), and their corresponding angles are equal due to the properties of a parallelogram.

(b) Both of them have a common hypotenuse, which is AC. This statement is incorrect. AC is not a hypotenuse because these are not right-angled triangles. AC is the diagonal of the parallelogram, not the hypotenuse.

(c) They lie between the same parallels and have equal base lengths.

Yes, both triangles lie between the same parallel lines (AB and CD) and have equal base lengths (AB and CD are equal in a parallelogram).

(d) The area of each of them is half of the area of the parallelogram ABCD.

Yes, the diagonal divides the parallelogram into two equal-area triangles. So the area of each triangle is half of the area of the parallelogram. Correct options: (a), (c), (d)

2. Will the triangles ABC and ADC overlap exactly when folded along AC?

Yes, when you fold the parallelogram along the diagonal AC, the triangles ∆ABC and ∆ADC will overlap exactly because they are congruent.

3. Which of the following quadrilaterals will result in complete overlap of the triangles when folded along the diagonals?

(a) Square Yes, folding along a diagonal of a square results in two congruent triangles that overlap exactly.

(b) Rectangle Yes, folding along a diagonal of a rectangle results in two congruent triangles that overlap exactly.

(c) Rhombus Yes, folding along a diagonal of a rhombus also results in two congruent triangles that overlap exactly.

(d) Trapezium No, folding a trapezium along a diagonal will not result in two congruent triangles unless it is an isosceles trapezium. Correct options: (a), (b), (c)

4 Steps for Shubhajit to cover T2 with T1 (in correct order): IV. Rotate T1 by 180°, clockwise/anti-clockwise, about the top-left corner of the parallelogram.

This is the first step to orient T1 for alignment with T2. V. Move T1 downward by a distance of H2.

After rotation, T1 needs to be moved downwards by the distance between the shorter sides (H2). VIII. Move T1 leftwards by a distance of H1.

Finally, move T1 leftwards by the distance between the longer sides (H1) to align it over T2. So, the correct steps in order are: IV → V → VIII