Pairs of Lines
Intersecting Lines
Here, we have the top view of the famous Flatiron Building in New York City. When we observe the two fronts of the building, what can be said? The two fronts of the building are at an angle (not parallel, as in the usual case) and they meet along a common edge. In geometric terms (3D), we can think of it as two planes at an angle to each other, meeting and sharing a number of points along the common edge.

In 2D geometry, two lines which have a



The legs of an easel (frame for holding painting canvas), a road merging/diverging (if we consider roads as straight lines) and grill bars on a window, what do all these have in common?
They are all examples of
Say, two lines l and m intersecting at O then O becomes their "common point" and the point of intersection.
If two lines intersect, do they always intersect at right angles?
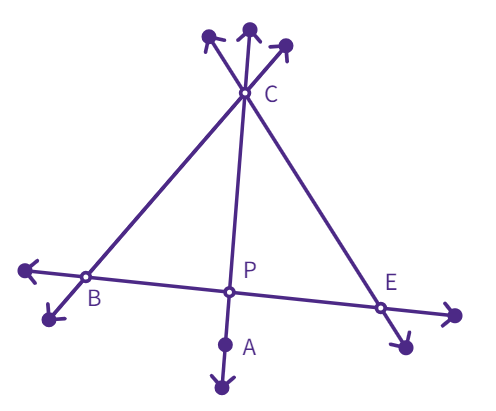
In the given figure, AC and BE intersect at P. AC and BC intersect at C, AC and EC intersect at C.
Should any two lines or line segments necessarily intersect?
Can you find two pairs of non-intersecting line segments in the figure?
If Yes, which ones ?
Can two lines intersect in more than one point?




A line that intersects two or more lines at distinct points is called a transversal. In the below figure, two non-parallel lines are crossed by a transversal line.

In the below figure, the line p is not a transversal, although it cuts two lines q and r. Why is that?
1. Find examples from your surroundings where lines intersect at right angles.
2. Find the measures of the angles made by the intersecting lines at the vertices of an equilateral triangle.
Solution:
In an equilateral triangle, all three sides are equal in length, and all three interior angles are equal as well.
Figure
AB = BC = CA
∠a + ∠b + ∠c =
This means tha: ∠a = ∠b = ∠c
∠a + ∠a + ∠a = 180°
∠a =
Therefore, measures of the angles made by the intersecting lines in an equilateral triangle are ∠a = 60°, ∠b = 60°, ∠c = 60°.
3. Draw any rectangle and find the measures of angles at the four vertices made by the intersecting lines
Solution:
Figure
AB =
∠a + ∠b + ∠c + ∠d =
∠a = ∠b = ∠c = ∠d
∠a + ∠a + ∠a + ∠a = 360°
∠a =
Therefore, the measures of angles at the four vertices made by the intersecting linesare ∠a = 90°, ∠b = 90°, ∠c = 90°, ∠d = 90°.
4. If two lines intersect, do they always intersect at right angles?
Solution:
Right angles, Obtuse angles and Acute angles
No, it is not necessary that lines always intersect at right angles. The lines may form an acute angle (another angle will be obtuse as to form linear pair)
Angles Made By a Transversal
In the figure below, two parallel lines say, 'l' and 'm' are cut by transversal line 'p'. The eight angles marked 1 to 8 have their special names:
(1) Interior angles: ∠AJI ∠CIJ ∠BIJ ∠DJI
(2) Exterior angles: ∠AJE ∠CIF ∠DJE ∠BIF
(3) Pairs of Corresponding angles: ∠AJE and ∠BIJ ∠EJD and ∠JIC ∠AJI and ∠BIF ∠DJI and ∠CIF
(4) Pairs of Alternate interior angles: ∠AJI and ∠CIJ ∠DJI and ∠BIJ
(5) Pairs of Alternate exterior angles: ∠AJE and ∠CIF ∠DJE and ∠BIF
(6) Pairs of interior angles on the same side of the transversal: ∠AJI and ∠BIJ ∠DJI and ∠CIJ
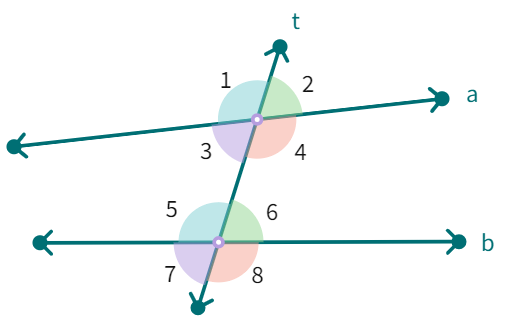
| Term | Diagram Example |
|---|---|
| Interior angles | ∠3, ∠ |
| Exterior angles | ∠1, ∠ |
| Pairs of Corresponding angles | ∠1 and ∠ ∠ ∠3 and ∠ ∠ |
| Pairs of Alternate interior angles | ∠ ∠4 and ∠ |
| Pairs of Alternate exterior angles | ∠1 and ∠ ∠ |
| Pairs of interior angles on the same side of the transversal | ∠ ∠ |
Note:
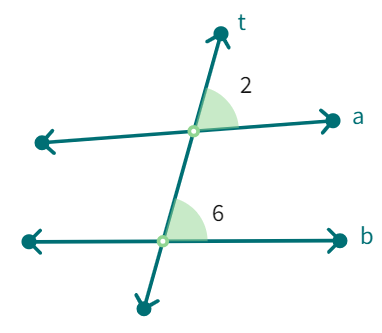
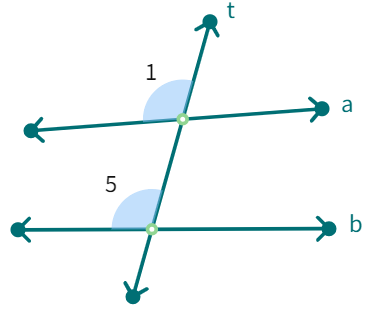
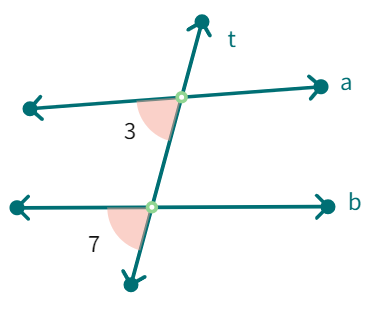
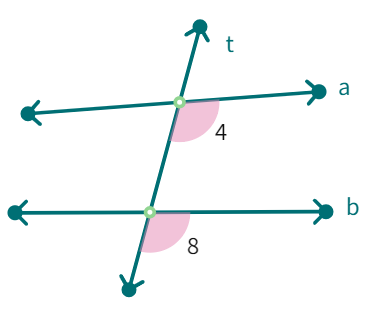
Corresponding angles: (like ∠1 and ∠5 ) include:
(i) different vertices
(ii) are on the same side of the transversal and
(iii) are in ‘corresponding’ positions (above or below, left or right) relative to the two lines.
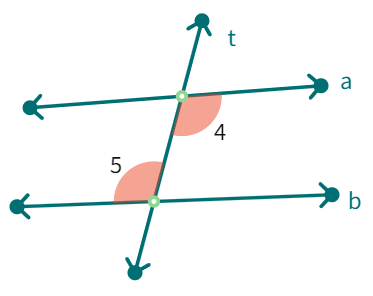
Alternate interior angles: (like ∠3 and ∠6)
(i) have different vertices
(ii) are on opposite sides of the transversal and
(iii) lie ‘between’ the two lines.
Classify the pair of angles in the following figures:




Actitvity: Take a ruled paper and draw a pair of parallel lines coinciding with the ink lines. Draw a random transverse line which cuts both the lines. Measure the corresponding angles.

This activity illustrates the following fact:
If two parallel lines are cut by a transversal, each pair of corresponding angles are equal in measure.
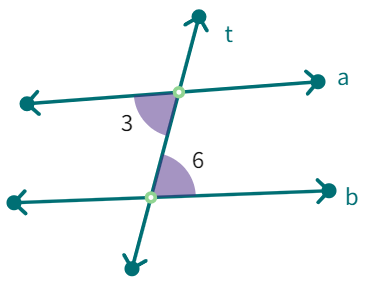
We can use this result to get another interesting result. Look at figure above.
When 't' cuts the parallel lines, m and n, we get : ∠3 = ∠7 (vertically opposite angles).
But also, ∠7 = ∠8 (corresponding angles).
Therefore, ∠3 = ∠
Similarly we can show that ∠1 = ∠
Thus, we have the following result:
If two parallel lines are cut by a transversal, each pair of alternate interior angles are equal
∠3 + ∠1 =
But ∠1 = ∠6 (A pair of
Therefore, we can say that ∠3 + ∠6 =
Similarly, ∠1 + ∠8 =
Thus, we obtain the following result:
If two parallel lines are cut by a transversal, then each pair of interior angles on the same side of the transversal are supplementary.
We can very easily remember these results while looking for relevant ‘shapes’.
The F-shape stands for corresponding angles.
The Z - shape stands for alternate angles.
1. Lines l || m with t is a transversal. Then ∠ x = ?
l || m
Solution:
If two parallel lines are cut by a transversal, then alternate interior angles are
60° and x is a pair of alternate interior angles
Therefore, we have: x =
2. Lines a || b with c is a transversal. Find the value of ∠ y = ?
a || b
Solution:
Here, line a is parallel to line b and they are cut by c, a transversal.
The angle y is equal to the angle of
Therefore, the value of angle y is
3. l1 ,l2 are two lines with 't' as a transversal. Is ∠ 1 = ∠2 ?
l1 and l2 are two lines
Solution:
If l1 and l2 are parallel, then by the Alternate Interior Angles Theorem, the alternate interior angles are congruent. Hence, ∠1 would be
Since, l1 and l2
4. Lines l || m with t is a transversal. Find ∠ z = ?
l || m
Solution:
In the given diagram, lines l and m are parallel, and t is a transversal. The angle 60° is given, and we need to find the measure of angle z.
Using the "Same Side Interior Angles Theorem", if two parallel lines are cut by a transversal, then the same side interior angles are
So, ∠60° + ∠z = 180° (as sum of interior angles on same side of transversal is 180°)
∠z = 180° - 60° =
Therefore, ∠z = 120°.
5.Lines l || m with 't' as a transversal. Find the value of ∠ x = ?
l || m
Solution:
Since, l || m and t is a transversal and ∠ x is
Therefore, angle x is equal to
Thus, ∠x = 120°
6. Lines l || m as well as p || q. Find the angle measures of a, b, c, d.
l || m, p || q
Solution:
Since, p || q and l is a transversal: a +
⇒ a = 180°- 60° =
Since l || m and q is a transversal
Observe ∠1.
∠a = ∠1 (pair of
Also ∠1 =
Now, ∠1 + ∠c =
⇒ 120° + ∠c =
⇒ ∠c = 180° - 120° =
⇒ ∠b = ∠c =
Hence, ∠a = 120°, ∠b = 60°, ∠c = 60°, ∠d = 120°
