Innings2
Create New Account

Sign in to Innings2

or

New Account     Reset Password     

Chapter 8: Triangles

    Introduction

    Similar Figures

    Similarity of Triangles

    Criteria for Similarity of Triangles

    Pythagoras’ Theorem

    Different Forms Of Theoretical Statements

    Summary

    Enhanced Curriculum Support

    Easy Level Worksheet

    Moderate Level Worksheet

    Hard Level Worksheet

Powered by Innings 2

Reset Progress

This will delete your progress and chat data for all chapters in this course, and cannot be undone!

Glossary

Select one of the keywords on the left…

Chapter 8: Triangles > Enhanced Curriculum Support

Enhanced Curriculum Support

This is a comprehensive educational resource designed to provide students with the tools and guidance necessary to excel. This support system is structured to cater to various aspects of learning, ensuring that students are well-prepared for academic challenges and practical applications of mathematical concepts. Some are the key benefits are mentioned below:

Comprehensive Learning: This holistic approach helps students gain a thorough understanding of the subject. Practical Application: The resources encourage students to apply mathematical concepts to real-life scenarios, enhancing their practical understanding and problem-solving skills.

Exam Preparedness: Sample Question Papers provide ample practice for exams. They help students familiarize themselves with the exam format and types of questions, reducing exam anxiety.

Sample Questions

About the Section

Sec A

(1) Give two different examples of pair of similar figures.

(2) In △ ABC, DE || BC, where AD = 2 cm, DB = 3 cm and AE = 4 cm, then AC is ......

(A) 5 cm

(B) 10 cm

(C) 6 cm

(D) 9 cm

(3) Among the following, the pair of triangles which are always similar is .....

(A) two isosceles triangles.

(B) two scalene triangles.

(C) two equilateral triangles.

(D) two right-angled triangles.

(4) Corresponding sides of two similar triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, then the area of the larger triangle is .....

(A) 108 cm2 (B) 72 cm2

(C) 36 cm2 (D) 90 cm2

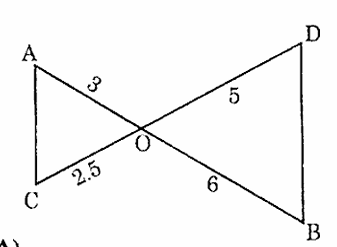
(5) Write the similarity criterion by which the given pair of triangles are similar.

Sec B

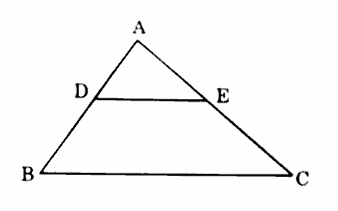
(1) The sides of a triangle measure 2sqt2, 4 and 26 units. Is it a right-angled triangle? Justify.

(2) In the given figure, ABC is a triangle. AD = 3 cm, DB = 5 cm, AE = 6 cm and EC = 10 cm. Is DE || BC ? Justify.

(3) In ΔABC, PQ||BC and AP=3x−19, PB=x−5, AQ=x−3, QC=3cm. Find x.

Sec C

(1) In a trapezium ABCD, AB || DC. If diagonals intersect each other at point 'O', then show that AOBO = CODO.

(2) ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point 'O'. Show that AOBO = CODO.

(3) In a rectangle ABCD, AB = 2x - y, BC = 15, CD = 2 and DA = x + 3y, then find the values of x and y.

(4) Construct an equilateral triangle XYZ of side 5 cm and construct another triangle similar to ΔXYZ, such that each of its sides is 45 of the sides of ΔXYZ.

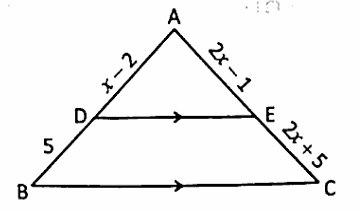
(5) In ΔABC, DE || BC. If AD = x – 2, DB = 5, AE = 2x – 1, EC = 2x + 5, then find the value of x.

Sec D

(1) Construct triangle ABC with BC = 7 cm, ∠B = 45° and ∠C = 60°. Then construct another triangle similar to △ ABC, whose sides are 35 times of the corresponding sides of △ ABC.

(2) Construct a triangle ABC with AB = 5.6 cm, BC = 7.2 cm and CA = 4.8 cm. Construct another triangle similar to △ ABC, whose sides are 35 times of the corresponding sides of △ ABC.

(3) Construct a triangle PQR, in which PQ=4cm, QR=6cm and ∠PQR=70°. Construct triangle such that each side of the new triangle is 34 of the triangle PQR.

Sec E

(1) Construct an isosceles triangle whose base is 6 cm and altitude is 3 cm. Then draw another triangle whose sides are 1 13 times the corresponding sides of the isosceles triangle.