Innings2
Create New Account

Sign in to Innings2

or

New Account     Reset Password     

Chapter 4: Basic Geometric Ideas

    Introduction

    Points

    A Line Segment

    A Line

    Ray

    Curves

    Angles

    Triangles

    Quadrilaterals

    Circles

    Exercise 4.1

    Exercise 4.2

    Exercise 4.3

    Exercise 4.4

    Exercise 4.5

    What Have We Discussed?

    Enhanced Curriculum Support

    Easy Level Worksheet

    Moderate Level Worksheet

    Hard Level Worksheet

Powered by Innings 2

Reset Progress

This will delete your progress and chat data for all chapters in this course, and cannot be undone!

Glossary

Select one of the keywords on the left…

Chapter 4: Basic Geometric Ideas > Curves

Curves

Take a piece of paper and just start doodling randomly whatever comes to your mind. The results of your random doodling are called curves.

Important Note:

‘Curve’ in everyday usage means “not straight”. In Mathematics, a curve can be straight.

We can draw some of these drawings without lifting the pencil from the paper and without the use of a ruler. These are all classified as curves and have different types.

  • Curves
    • Based on Presence of Intersection Points
      • Simple Curves
      • Non-Simple Curves

If a curve does not cross itself, then it is called a simple curve. A simple curve changes its direction but does not cross itself.

It can be open and closed. If a curve does cross itself, it is a non-simple curve.

Examples for simple closed curves -Circle, ellipse.

Out of the seven below given figures, classify as "Simple"/ "Not Simple" / "Open" Curve.

Simple
Not Simple
Open

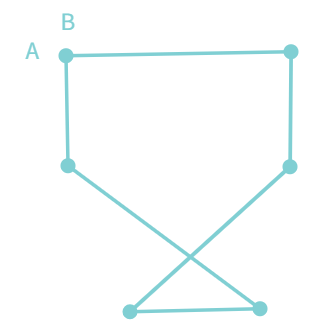
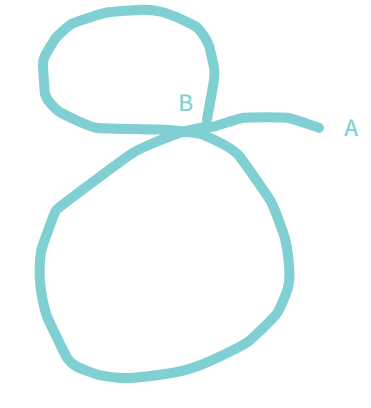
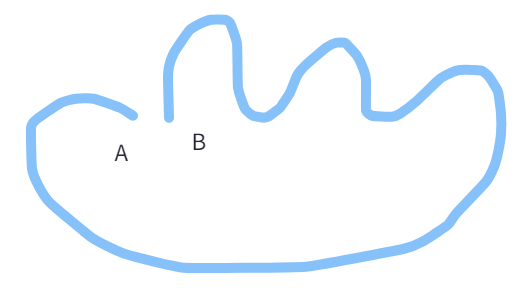
Let's see in detail?

Position in a figure

Think about this: When we see a house or a building, there is often a fence or a compound wall that separates the building from the road and the rest of the surrounding land. A division like that causes the land to be separated into parts- inside the fencing, exactly on the fence and outside the fence. We cannot enter the building without crossing the fence or the gate/ main entrance of the building.

Similarly, when we have a closed curve on a piece of paper and we randomly select points, we can classify the points into three types:

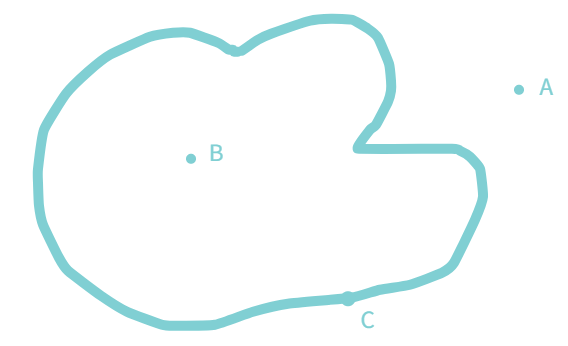
  • (i) interior (‘inside’) points
  • (ii) boundary (‘on’) points
  • (iii) exterior (‘outside’) points

In the below given figure, B is the point , A is the and C is .

The interior of a curve together with its boundary is called its region.

Region enclosed by a closed curve

Polygons

A figure is a polygon if it is a simple figure made up entirely of .

Distinguish the following figures as a polygon or not:

Sides, vertices and diagonals

Polygon with six sides i.e. Hexagon

The line segments forming a polygon are called its Sides

Above polygon ABCDEF has the sides: AB, BC, CD, DE EF and FA.

The corners are usually named in order.

The meeting point of a pair of adjacent sides is called its vertex .

Sides EF and FA meet at F, so F is a vertex of the polygon ABCDEF. So, are points like A, B,C etc.

Any two sides with a common end point are called the adjacent sides of the polygon.

Are the sides AB and BC adjacent?

How about AF and DC?

The end points of the same side of a polygon are called the adjacent vertices. Vertices E and D are adjacent, whereas vertices A and D are not adjacent vertices.

Consider any pairs of vertices which are not adjacent and join them with a line segment.

The line segment joining two non-adjacent vertices in a polygon is called the diagonal of the polygon.

So, in the above figure- AD, BE, CF etc. are diagonals.

How many total diagonals does the polygon have?

If we try to join adjacent vertices with a line segment, what is the result? The line segment will be a .