Equivalent Fractions

Equivalent fractions are the fractions that have different numerators and denominators but are equal to the same value. For example, 2/4 and 3/6 are equivalent fractions, because they both are equal to the .

A fraction is a part of a whole. Equivalent fractions represent the same portion of the whole.

These fractions are 12, 24, 36 representing the parts taken from the total number of parts. If we place the pictorial representation of one over the other they are found to be equal. You can try it out below. When you place the squares on top of each other you will find that the green and red parts overlap exactly though there are different number of green and red pieces in each image.

All these fractions are Equivalent?

Instruction

1. Are 13 and 27 ; 25 and 27 ; 29 and 627 equivalent? Give reason.

13 and 27 is not eqivalent fraction because is not exactly divisible by 3.

27.

27 is not equivalent fraction of 25 because is not exactly divisible by 5.

627.

29 will be equivalent to 627 because if we multiply 29 by in both numerator and denominator then ans will be 627.

Instruction

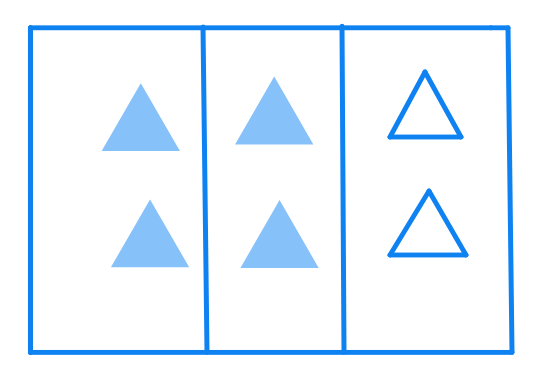
Drag and drop the equivalent fractions of 12 into the box.

Equivalent Fraction

Not a Equivalent Fraction

Identify the fractions in each. Are these fractions equivalent?

(i)

(ii)

(iii)

(iv)

Why do the equivalent fractions represent the same part of a whole?

How can we obtain one from the other?

Let see an example?

12=

To obtain equivalent fractions of a fraction, we have to either multiply or divide the same number in both the numerator and denominator.
Let us multiply 2 in both the numerator and denominator and then we find the fraction is
Simplifying this fraction then the fraction is
Let us multiply 3 in both the numerator and denominator.
Multiply the fractions and the fraction is .
Simplifying this fraction then we get the fraction is
Let us multiply 4 in both the numerator and denominator.
Multiply this fraction then we get the answer is
Divide the fraction again and we get the fraction as
Hence, we have found the equivalent fractions of 12.

Rajni says that equivalent fractions of 13

13=

To obtain equivalent fractions of a fraction, we have to either multiply or divide the same number in both the numerator and denominator.
Let us multiply 2 in both the numerator and denominator and then we find the fraction is
Simplifying this fraction then the fraction is
Let us multiply 3 in both the numerator and denominator.
Multiply the fractions and the fraction is .
Simplifying this fraction then we get the fraction is
Let us multiply 4 in both the numerator and denominator.
Multiply this fraction then we get the answer is
Divide the fraction again and we get the fraction as
Hence equivalent fractions of 13 have been found.

Do you agree with her?

Rajni is correct in her method of finding equivalent fractions because she follows the rule that to get an equivalent fraction, you multiply both the numerator and the denominator of a given fraction by the same number.

Find five equivalent fraction for below numbers.

(i) 23

Instruction

To find equivalent fractions of 23, multiply both the numerator and denominator by different numbers.

Let us multiply 2 in both the numerator and denominator 23 × = =

Let us multiply 3 in both the numerator and denominator 23 × = =

Let us multiply 4 in both the numerator and denominator 23 × = =

Let us multiply 5 in both the numerator and denominator 23 × = =

Let us multiply 6 in both the numerator and denominator 22 × = =

So, five equivalent fractions of 23 are : 46 , 69 , 812 , 1015 and 1218.

(ii) 15

To find equivalent fractions of 15, multiply both the numerator and denominator by different numbers.

Let us multiply 2 in both the numerator and denominator 15 × = =

Let us multiply 3 in both the numerator and denominator 15 × = =

Let us multiply 4 in both the numerator and denominator 15 × = =

Let us multiply 5 in both the numerator and denominator 15 × = =

Let us multiply 6 in both the numerator and denominator 15 × = =

So, five equivalent fractions of 15 are : 210 , 315 , 420 , 525 and 630.

(iii) 35

To find equivalent fractions of 35, multiply both the numerator and denominator by different numbers.

Let us multiply 2 in both the numerator and denominator 35 × = =

Let us multiply 3 in both the numerator and denominator 35 × = =

Let us multiply 4 in both the numerator and denominator 35 × = =

Let us multiply 5 in both the numerator and denominator 35 × = =

Let us multiply 6 in both the numerator and denominator 35 × = =

So, five equivalent fractions of 35 are : 610 , 915 , 1220 , 1525 and 1830.

(iv) 59

To find equivalent fractions of 59, multiply both the numerator and denominator by different numbers.

Let us multiply 2 in both the numerator and denominator 59 × = =

Let us multiply 3 in both the numerator and denominator 59 × = =

Let us multiply 4 in both the numerator and denominator 59 × = =

Let us multiply 5 in both the numerator and denominator 59 × = =

Let us multiply 6 in both the numerator and denominator 59 × = =

So, five equivalent fractions of 59 are : 1018 , 1527 , 2036 , 2545 and 3054.

Is there any other way to obtain equivalent fractions?

46 is shaded here

23 is shaded here

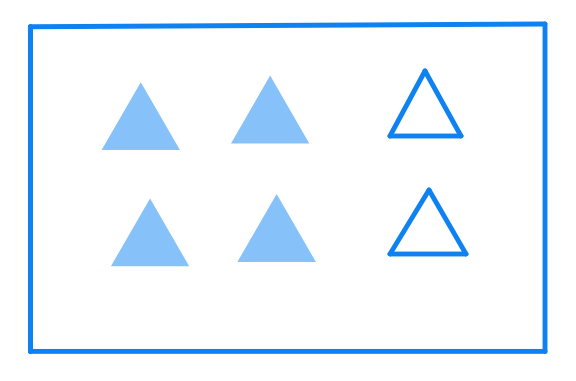
These include equal number of shaded things i.e. 46 = 23 = 4÷26÷2

To find an equivalent fraction, we may divide both the numerator and the denominator by the same number.

One equivalent fraction of 1215 is 12÷315÷3 =

Can you find an equivalent fraction of 915 having denominator 5 ?

915

We divide both the numerator and the denominator of 915 by and then we get the fraction is
Divide the fraction with 3
Hence is the required equivalent fraction.
We found the answer.

Find the equivalent fraction of 25 with numerator 6.

23=

We know 2 × 3 = .
This means we need to multiply both the numerator and the denominator by 3 to get the equivalent fraction.
We get the fraction is .
is the required equivalent fraction.

Find the equivalent fraction of 1535 with denominator 7.

1535

We divide both the numerator and the denominator of 1535 by and then we get the fraction is
divide the fraction with 5
Hence is the required equivalent fraction..

Let us now note an interesting fact about equivalent fractions. For this, complete the given table.

Equivalent fractions	Product of the numerator of the 1st and the denomenator of the 2nd	Product of the numerator of the 2nd and the denomenator of the 1st
13 = 39	1 × 9 =	3 × 3 =
45 = 2835	4 × 35 =	5 × 28 =
14 = 416	× = 16	× = 16
23 = 1015	2 × = 30	× 10 = 30
37= 2456	× =	7 × 24 =

What do we infer?

The product of the numerator of the first and the denominator of the second is to the product of denominator of the first and the numerator of the second in all these cases. These two products are called cross products.

This rule is helpful in finding equivalent fractions.

Find the equivalent fraction of 29 with denomiantor of 63.

Instruction

We need 29 with denominator 63.

For this, we should have 9 × y = × 63.

But 63 = × 9 , So 9 × y = 2 × (7 × 9) = × 9

By comparison, y = 14. Therefore, 29 = .

Given the fraction 3654, let us try to get an equivalent fraction in which the numerator and the denominator have no common factor except 1.

How do we do it?

We see that both 36 and 54 are divisible by .

3654 = 36 ÷ 254 ÷ 2 = .

But 18 and 27 also have common factors other than one.

The common factors are , , with the highest one being .

Therefore, 1827 = 18 ÷ 927 ÷ 9 =

Now 2 and 3 have no common factor except 1; we say that the fraction 23 is in the simplest form.

A fraction is said to be in the simplest (or lowest) form if its numerator and denominator have no common factor except 1.

The shortest way to find the equivalent fraction in the simplest form is to find the HCF of the numerator and denominator, and then divide both of them by the HCF.

The equivalent fractions given here are quite interesting.

Each one of them uses all the digits from 1 to 9 once!

26 = 39 =

24 = 36 =

Try to find two more such equivalent fractions.

To find such fractions, we need to create fractions where both the numerator and the denominator use unique digits from 1 to 9 and the fractions are equivalent.

12 = 48 = =

13 = 412 =

1. Write the simplest form.

(i)1575

1575=

It can be observed that is the highest common factor of 15 and 75.
Divide the numerator and denominator by the highest common factor 15.
Hence, we get the fraction is .
We have found the answer.

(ii)1672

1672=

It can be observed that is the highest common factor of 16 and 72.
Divide the numerator and denominator by the common factor 8.
Hence, we get the fraction is .
We have found the answer.

(iii)1751

1751=

It can be observed that is the highest common factor of 17 and 51.
Divide the numerator and denominator by the common factor 17.
Therefore, we get the fraction is .
We have found the answer.

(iv)4228

4228=

It can be observed that is the highest common factor of 42 and 28.
Divide the numerator and denominator by the common factor 14.
Therefore, we get the fraction is .
We have found the answer.

(v)8024

8024=

It can be observed that is the highest common factor of 80 and 24.
Divide the numerator and denominator by the common factor 8.
Therefore, we get the fraction is .
We have found the answer.

2. Is 4964 in its simplest form?

Instruction

Is 4964 in its simplest form ?

We know that: 49 and 64 has common divisor.

So, , 4964 is in its simplest form.

Fractions and Decimals

Glossary

Equivalent Fractions

Sign in to Innings2

Fractions and Decimals

Reset Progress

Glossary

Equivalent Fractions