Exercise 3.3

1. Write the missing numbers in the factor tree for 90?

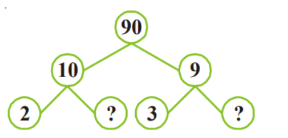
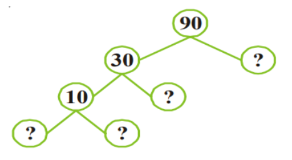
Factors of 90 are integers that can be divided evenly into 90. There are 12 factors of 90 of which 90 itself is the biggest factor and its prime factors are , , and . The Prime Factorization of 90 is 2×32×5.

Factors of 90: , , , , , , , , , , and .

2. Factorise 84 by division method?

We can find the factor pairs, by multiplying two numbers in a pair to get the original number as 84, such as;

1 × = 84

2 × = 84

3 × = 84

4 × = 84

6 × = 84

7 × = 84

Therefore, the factor pairs are (1, ), (2, ), (3, ), (4, ), (6, ) and (7, ). Thus, with this we can evaluate the unique factors of number 84 as given below;

Factors of 84 : , , , , , , , , , , and .

3. Write the greatest 4 digit number and express it in the form of it's prime factors?

The largest 4-digit number is .

We will see the prime factors of 9999 to answer this question.

The prime factors of 9999 are , , and .

We can express 9999 as the product of its prime factors, that is, 9999 = 32 × × .

Therefore, we can write 9999 = 32 × 11 × 101.

4. I am the smallest number, having four different prime factors. Can you find me?

is the smallest number having four different prime factors.

The smallest number having four different prime factors will be the product of the first four prime numbers.

Explanation: The first four prime numbers are , , and .

The required number will be the product of these numbers. 2 × 3 × 5 × 7 = 210.

Hence, 210 is the smallest number having four different prime factors.