Convex and concave polygons

We are also aware that a simple closed curve made up of only line segments is called a .

We know that polygons have a classification based on the number of sides it if made up of. However, there is another that helps in differentiating them.

We know that polygons consist of a number of diagonals. Based on the position of the diagonals we get two types of polygons:

Convex Polygons:

Polygons which have all theirs diagonals, contained within the interiors of their boundaries are known as convex polygons. In other words, any line segment joining any two vertices must lie wholly in the interior of the polygon.

Concave Polygons:

When the contrary is true i.e. when atleast one diagonal lies in the exterior region of the polygon, the polygon is classified as a concave polygon.

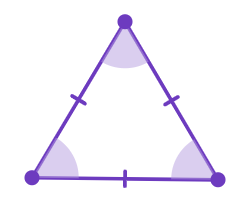
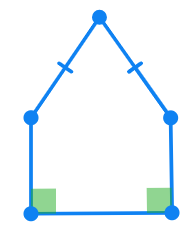
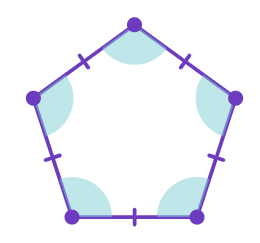
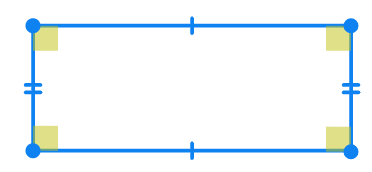
Let's revise this concept by correctly classifying the below given figures.

Instructions

Concave Polygon

Convex Polygon

In this section, we will be dealing with convex polygons only.

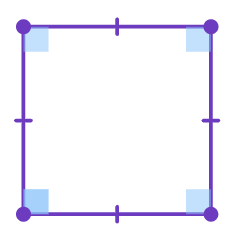
Regular and irregular polygons

We know that a regular polygon is both ‘equiangular’ and ‘equilateral’. For example: a square has sides of equal length and angles of equal measure. Hence, it is a polygon.

A rectangle is equiangular but not equilateral. Thus, it is .

Note: Sides with hash marks (| or ||) denotes equal sides.

Instructions