Exercise 5.1
1. Find the ratio of the following
i. Smita works in office for 6 hours and Kajal works for 8 hours in her office. Find the ratio of their working hours.
Solution:
Ratio of Smita's working hours to Kajal's working hours = 6 hours : 8 hours
We can simplify this ratio by divding both sides by their greatest common divisor, which is
6 : 8 = (
Therefore, the ratio of their working hours is
ii. One pot contains 8 litres of milk while the other contains 750 millilitres.
Solution:
First, we need to convert the quantities to the same unit. Let's convert litres to millilitres. We know that 1 litre =
So, 8 litres = 8 × 1000 millilitres =
Now we can find the ratio:
Ratio of milk in the first pot to the second pot =
We can simplify this ratio by dividing both sides by their greatest common divisor, which is
8000 : 750 = (
Therefore, the ratio of the quantities of milk is
iii. Speed of a cycle is 15 km/h and the speed of a scooter is 30 km/h.
Solution:
Ratio of speed of cycle to speed of scooter = 15 km/h : 30 km/h
We can simplify this ratio by dividing both sides by their greatest common divisor, which is
15 : 30 = (
Therefore, the ratio of their speeds is
2. If the compound ratio of 5:8 and 3:7 is 45:x. Find the value of x.
Solution:
The compound ratio of two ratios a:b and c:d is given by
In this case, the compound ratio of 5:8 and 3:7 is (5 × 3) : (8 × 7) =
We are given that this compound ratio is equal to
Therefore: 15 : 56 = 45 : x
We can set up a proportion:
Cross-multiply:
15x =
x =
x =
Therefore, the value of x is 168.
3. If the compound ratio of 7:5 and 8:x is 84:60. Find x.
Solution:
The compound ratio of 7:5 and 8:x is (7×8):(5×x) =
We are given that this compound ratio is 84 : 60. So:
56 : 5x = 84 : 60
We can set up a proportion:
Cross-multiply:
56 ×
x =
x =
Therefore, the value of x is 8.
4. The compound ratio of 3:4 and the inverse ratio of 4:5 is 45:x. Find x.
Solution:
The inverse ratio of 4:5 is
The compound ratio of 3 : 4 and 5 : 4 is (3 × 5) : (4 × 4) =
We are given that this compound ratio is equal to 45 : x. Therefore:
15 : 16 = 45 : x
We can set up a proportion:
Cross-multiply:
15x = 45 × 16
15x =
x =
x =
Therefore, the value of x is 48.
5. In a primary school there shall be 3 teachers to 60 students. If there are 400 students enrolled in the school, how many teachers should be there in the school in the same ratio?
Solution:
The ratio of teachers to students is 3 : 60, which can be simplified to 1:20 (by dividing both sides by 3).
This means for every
If there are 400 students, we can set up a proportion to find the number of teachers (let's call it 'x'):
Cross-multiply:
x =
x =
Therefore, there should be
6. In the adjacent ΔABC, write all possible ratios by taking measures of sides pair wise.
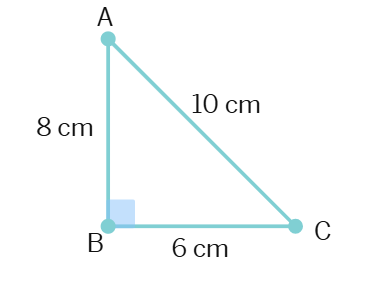
(Hint : Ratio of AB : BC = 8 : 6)
Solution:
Given the side lengths AB = 8, BC = 6, and AC = 10 (though AC isn't explicitly used in the ratios, it's good to note we have a 3-4-5 triangle scaled by 2).
We can form the following ratios by taking the sides pairwise, expressed as fractions:
7. If 9 out of 24 students scored below 75% marks in a test. Find the ratio of students who scored below 75% marks to the students who scored 75% and above marks.
Solution:
Students scoring below 75% marks:
Total students:
Students scoring 75% and above marks:
Ratio of students scoring below 75% to students scoring 75% and above:
We can simplify this ratio by dividing both sides by their greatest common divisor, which is
9:15 = (
Therefore, the required ratio is 3:5.
8. Find the ratio of the number of vowels in the word 'MISSISSIPPI' to the number of consonants in the simplest form.
Solution:
The word MISSISSIPPI has
Vowels: I, I, I, I (
Consonants: M, S, S, S, S, P, P (
Ratio of vowels to consonants:
Since 4 and 7 have no common factors other than 1, the ratio is already in its simplest form.
Therefore, the ratio of vowels to consonants is 4:7.
9. Rajendra and Rehana own a business. Rehana receives 25% of the profit each month. If Rehana received ₹2080 in a particular month, what is the total profit in that month?
Solution:
Let the total profit in that month be 'P'.
Rehana receives 25% of the profit, which is equal to ₹
We can express this as an equation:
25% of P = ₹ 2080
P = ₹
P = ₹
Therefore, the total profit in that month was ₹8320.
10. In triangle ABC, AB = 2.2 cm, BC = 1.5 cm and AC = 2.3 cm. In triangle XYZ, XY = 4.4 cm, YZ = 3 cm and XZ = 4.6 cm. Find the ratio AB : XY, BC : YZ, AC : XZ. Are the lengths of corresponding sides of ΔABC and ΔXYZ in proportion?
Solution:
Ratio AB : XY = 2.2 cm : 4.4 cm =
Ratio BC : YZ = 1.5 cm : 3 cm =
Ratio AC : XZ = 2.3 cm : 4.6 cm =
Since all the corresponding sides have the same ratio (1:2), the lengths of the corresponding sides of ΔABC and ΔXYZ
Therefore, the answer is
11. Madhuri went to a super market. The price changes are as follows. The price of rice reduced by 5% jam and fruits reduced by 8% and oil and dal increased by 10%. Help Madhuri to find the changed prices in the given table.
| Item | Original Price/Kg | Changed Price |
|---|---|---|
| Rice | ₹ 30 | |
| Jam | ₹ 100 | |
| Apples | ₹ 280 | |
| Oil | ₹ 120 | |
| Dal | ₹ 80 |
Solution:
Rice: Reduced by 5%. Changed price = ₹
Jam: Reduced by 8%. Changed price = ₹
Apples: Reduced by 8%. Changed price = ₹
Oil: Increased by 10%. Changed price = ₹
Dal: Increased by 10%. Changed price = ₹
12. There were 2075 members enrolled in the club during last year. This year enrolment decreased by 4%.
(a). Find the decrease in enrolment.
Solution:
Decrease in enrolment = 4 % of 2075 =
=
Therefore, the decrease in enrolment is 83 members.
(b) How many members are enrolled during this year?
Solution:
Members enrolled last year:
Decrease in enrolment:
Members enrolled this year: Members enrolled last year - Decrease in enrolment
= 2075 - 83
=
Therefore, 1992 members are enrolled during this year.
13. A farmer obtained a yielding of 1720 bags of cotton last year. This year she expects her crop to be 20% more. How many bags of cotton does she expect this year?
Solution:
Increase in yield = 20 % of 1720 bags
=
=
=
Expected yield this year = Last year's yield + Increase in yield
=
=
Therefore, the farmer expects to yield 2064 bags this year.
14. Points P and Q are both on the line segment AB and on the same s> ide of its m> idpoint. P div> ides AB in the ratio 2:3, and Q div> ides AB in the ratio 3:4. If PQ = 2, then find the length of the line segment AB.
Solution:
Let the length of AB be 'x'.
Point P:
Point Q:
Since P and Q are on the same side of the midpoint, and the ratios indicate P is closer to A than Q is, we know that AP
Therefore, PQ =
PQ =
2 = (15x - 14x)/
2 =
x = 2 ×
x =
Therefore, the length of the line segment AB is 70 units.
