Exercise 2.2
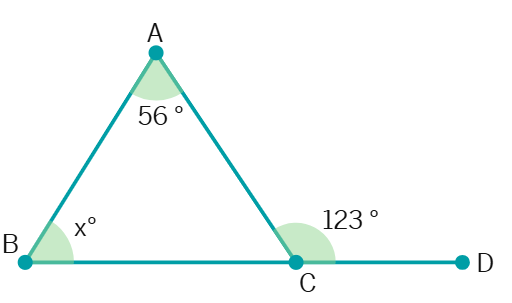
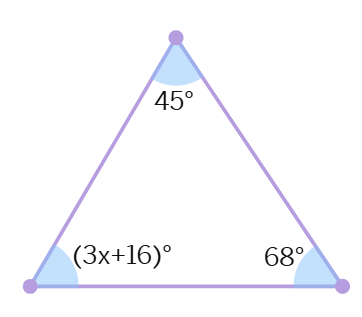
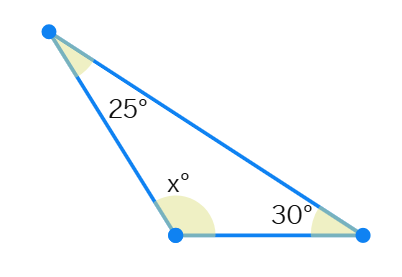
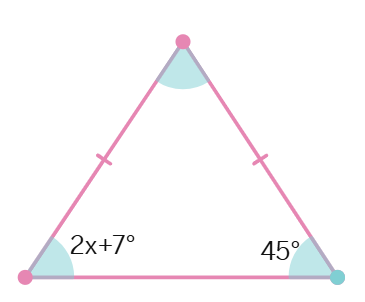
2. The difference between two numbers is 8. If 2 is added to the bigger number, the result will be three times the smaller number. Find the numbers.
Solution:
Let the two numbers be x and y, where x is the bigger number.
Given: x - y = 8 and x + 2 = 3y
From equation (1), x =
Substituting this into equation (2):
(y + 8) + 2 = 3y
y +
y =
Substituting y = 5 back into x = y + 8:
x = 5 + 8
x =
The two numbers are 13 and 5.
3. What are those two numbers whose sum is 58 and difference is 28?
Solution:
Let the two numbers be x and y.
Given: x + y = 58 and x - y = 28
Adding equations (1) and (2):
x =
Substituting x = 43 into equation (1):
43 + y = 58
y =
The two numbers are 43 and 15.
4. The sum of two consecutive odd numbers is 56. Find the numbers.
Solution:
Let the two consecutive odd numbers be x and (x + 2).
Given: x + (x + 2) = 56
2x =
x =
The numbers are 27 and 29.
5. The sum of three consecutive multiples of 7 is 777. Find these multiples. (Hint: Three consecutive multiples of 7 are ‘x’, ‘x + 7’, ‘x + 14’).
Solution:
Let the three consecutive multiples of 7 be x,
Given:
x + (x + 7) + (x + 14) = 777
3x + 21 = 777
3x =
x =
The multiples are 252,
6. A man walks 10 km, then travels a certain distance by train and then by bus as far as twice by the train. If the whole journey is of 70km, how far did he travel by train?
Solution:
Let the distance traveled by train be x km.
The distance traveled by bus is
Total distance = Walking distance + Train distance + Bus distance
70 = 10 +
x =
The man traveled 20 km by train.
7. Vinay bought a cake and cut it into three pieces. When he weighed the first piece he found that it was 7g lighter than the second piece and 4g heavier than the third piece. If the whole cake weighed 300g. How much d> id each of the three pieces weigh?
Solution:
Let the weight of the first piece be x g.
Weight of the second piece = x +
Weight of the third piece = x -
Total weight = x + (x + 7) + (x - 4) =
3x =
x =
Weight of the first piece = 99 g
Weight of the second piece = 99 + 7 =
Weight of the third piece = 99 - 4 =
8. The distance around a rectangular field is 400 meters. The length of the field is 26 meters more than the breadth. Calculate the length and breadth of the field?
Solution:
Let the breadth be b meters and the length be l meters.
Given:
From (1): l + b =
Substituting (2) into this: (b + 26) + b = 200
2b =
b =
l = b + 26 = 87 + 26 =
Thus, Length = 113 meters, Breadth = 87 meters.
9. The length of a rectangular field is 8 meters less than twice its breadth. If the perimeter of the rectangular field is 56 meters, find its length and breadth?
Solution:
Let the breadth be b meters and the length be l meters.
Given: l =
Substituting (1) into (2): 2(2b - 8 + b) = 56
2(3b - 8) = 56
6b =
b =
l = 2b - 8 = 2(12) - 8 =
Thus, Length = 16 meters, Breadth = 12 meters.
10. Two equal sides of a triangle are each 5 meters less than twice the third side. If the perimeter of the triangle is 55 meters, find the length of its sides?
Solution:
Let the third side be x meters.
The two equal sides are each
Perimeter = x + (2x - 5) + (2x - 5) =
5x =
x =
The sides are 13 meters, 21 meters, and 21 meters.
11. Two complementary angles differ by 12°. Find the angles?
Solution:
Let the two angles be x and y.
Given: x + y =
Adding (1) and (2): 2x =
x =
y = 90 - x = 90 -
The angles are 51° and 39°.
12. The ages of Rahul and Laxmi are in the ratio 5:7. Four years later, the sum of their ages will be 56 years. What are their present ages?
Solution:
Let Rahul's age be 5x and Laxmi's age be 7x.
Four years later: Rahul's age =
(5x + 4) + (7x + 4) =
12x =
x =
Rahul's age = 5x = 5(4) =
Laxmi's age = 7x = 7(4) =
13. There are 180 multiple choice questions in a test. A cand> idate gets 4 marks for every correct answer, and for every un-attempted or wrongly answered question one mark is deducted from the total score of correct answers. If a cand> idate scored 450 marks in the test how many questions d> id he answer correctly?
Solution:
Let the number of correct answers be x.
Number of incorrect/unattempted questions =
Marks for correct answers =
Marks deducted = 180 - x
Total score = 4x - (180 - x) =
4x -
5x =
x =
The candidate answered 126 questions correctly.
14. A sum of ₹500 is in the form of denominations of ₹5 and ₹10. If the total number of notes is 90 find the number of notes of each denomination. (Hint: let the number of 5 rupee notes be ‘x’, then number of 10 rupee notes = 90–x)
Solution:
Let the number of ₹5 notes be x.
Number of ₹10 notes =
Total amount = 5x +
5x +
900 -
x =
Number of ₹ 5 notes = 80
Number of ₹ 10 notes = 90 - 80 =
