Polygons

School districts need an accurate estimate of the number of students that may attend their schools. Below is a map of primary schools in London. In general, students attend the school closest to where they live. Click anywhere on the map to see the distance between that point and all the schools on the map.

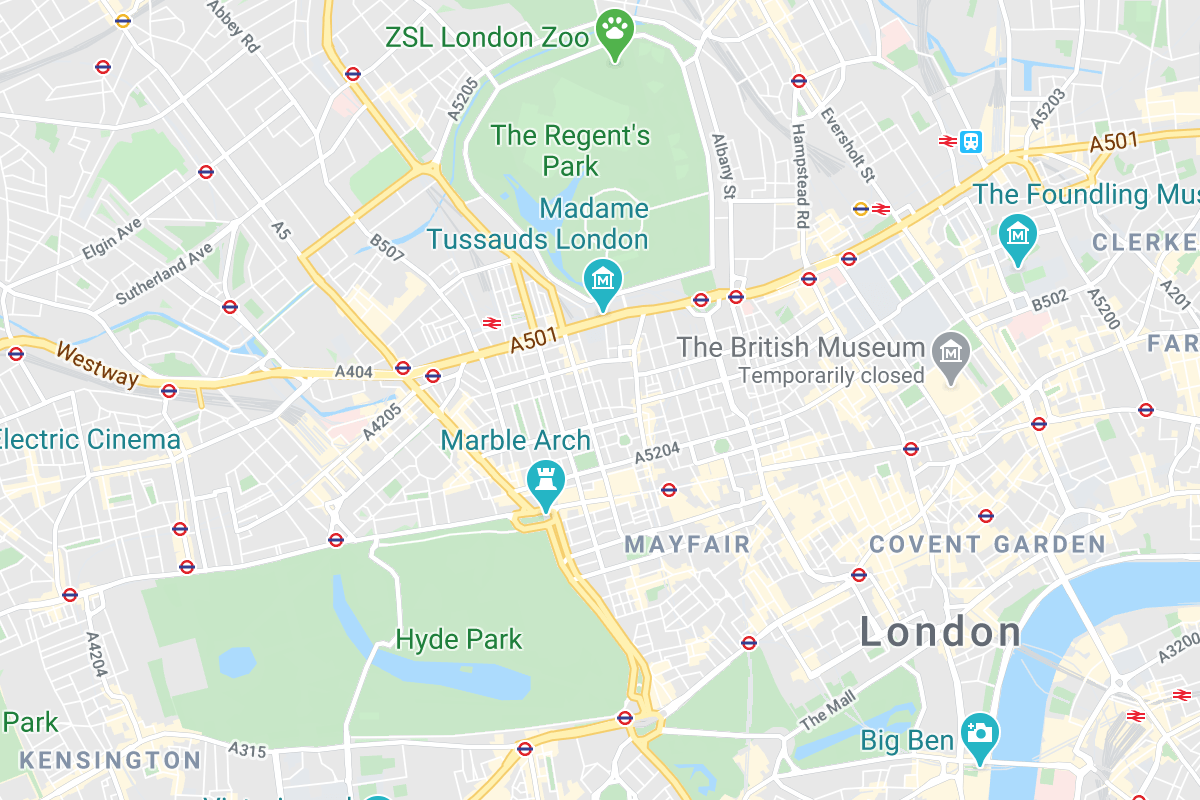
Pick 4 other points on the map.

Create voronoi diagram

We’ve just made a Voronoi diagram. Each region contains all the points on the map that are closest to the school in that region. Click a few spots in different regions to check.

The first person to think about these things was probably Rene Descartes 400 years ago - he was a famous philosopher too! But they’re named after a Russian mathematician, Gregory Feodosevich Voronoy. Physician John Snow used a version of a Voronoi diagram in 1854 during a cholera epidemic In London to locate an infected water pump on Broad Street in London

In our example, using a Voronoi diagram can help schools make estimates of how many students will attend. In London, about 1500 people live in each square kilometer. To use this statistic, we first need to first know the area perimeter of each region in the diagram.

Some of these regions are shapes we’ve learned about in previous chapters. This shape is a triangle and we can find the area by doing xbasexheight.

Click on the side of the triangle you want to use as the base.

Now draw in the height that corresponds with the base you selected.

The area of this triangle is [TODO] square km km.

1500 people1 square km= peopleTODO square km

[TODO] people live closest to that school and that can be a good starting point for the school to use to estimate how many students might attend that school. Next, the schools would want to use other statistics to estimate how many of those people are elementary aged students.

The other regions are more complicated. Some have 4 sides. Some have 5 sides. And some have 6 sides.

All of these regions in the Voronoi diagram are examples of polygons. A polygon is a closed, two-dimensional shape with straight sides that do not cross each other. A polygon does not have any holes in the shape. Click on a card below and drag it to the “Polygon” or “Non Polygon” side.

A regular polygon has all equal all different side lengths.

Let’s revisit the Voronoi diagram and find out how many people live in one of the regions with 5 sides. Note the region outlined in white in the image below.

Just by looking at this region, it seems that more less students will attend the school in this region than the school in the triangular region we explored above. The region looks similar in size, so it’s hard to be sure just by looking. Let’s find its area by splitting it up into rectangles and triangles and compare the area to the area of the triangular region.

[TODO]: People equation

So, indeed more students will likely attend the school in the pentagon region than the triangular region.

We give different names to polygons based on how many sides they have. You may remember some of the names. Drag the names on top of the correct shapes.

Polygons in real life

Let’s practice using these names by looking at some examples of polygons out in the world.

The Dome of the Rock is an Islamic Shrine in the Old City of Jerusalem. Built in 692 BCE, the base is a regular octagon pentagon hexagon.

The Giant’s Causeway in Northern Ireland is made up of over 40,000 polygonal basalt (a type of igneous rock) columns sticking out of the sea. The column outlined in white in the photo is a hexagon pentagon octagon.

Most traffic signs are polygons - some regular and some irregular:

Polygons show up in all sorts of natural objects - honeycomb and starfish - to name a few. The 10-sided starfish is a decagon nonagon octagon:

The ground of a dried out desert, the skin patterns on giraffes, and dragonfly wings look strikingly similar to Voronoi diagrams!

Lastly, many flags use polygons. Drag the name of each country to the correct flag. Just make a guess if you’re not sure!

The hexagons in the South African flag and the pentagon in the Nepalese flag may not appear to be the standard image you may have in your head of a pentagon and a hexagon. Move around the vertices (these are the points where the edges meet) in the regular polygons below to make some irregular polygons of your own.

Tangram

Below are 7 polygons. Move and rotate the polygons to completely fill in the square

Area of Polygons

Now that we have a firm understanding of polygons, let’s revisit thinking about the area of polygons. The football below is made up of 12 black pentagons hexagons octagons and 20 white hexagons pentagons octagons. The mathematical name for this is 3D shape is a truncated icosahedron. A football is slightly more rounded than a true truncated icosahedron since the pentagons and hexagons bulge out due to the air pressure inside.

Most footballs are made of synthetic leather. Manufacturers make so many footballs that they pay great attention to the amount of synthetic leather they need to produce each football. Let’s find the amount of synthetic leather needed to make one professional football.

Recently, football manufacturers have begun to experiment with different shaped panels other than hexagons and pentagons. Here are some of the official footballs from the recent men’s World Cup tournaments.

While these designs are creative and interesting, some studies have shown that the different shaped panels impact how the ball travels through the air!

Below is a polygon from a different Voronoi diagram. Each grid represents 1 square kilometer. Let’s find the area of this region in a few different ways.

Coming Soon!

No matter which approach we take, the area of the pentagon is 27.5 square units!

Curry’s Paradox

Throughout our work on area, we have often used the idea that as parts of a shape are moved around, the area stays the same - as long as the pieces don’t overlap and all the pieces are used.

We’ve made a triangle with a base of 13 units and a height of 5 units. The area of this triangle is square units. So, the area of these 4 pieces must also be square units.

This triangle also has a base of and a height of so the area of the triangle has stayed the same at 32.5 square units. However, now it seems the area of the 4 pieces is one less than more than the area of the triangle! How can this be when we expect the area of shapes to stay the same when we move them around? Move the slider back and forth to see this again.

This situation is called Curry’s Paradox. A paradox is a statement or situation that contradicts itself. This paradox, created by American mathematician Haskell Curry, is that the area of the 4 pieces first seemed to equal 32.5 square units and then they seem to equal 31.5 square units!

Let’s take the shape apart and find the area of each piece to help us see what’s happening here.

The red triangle has a base of 8 and a height of 3, so the area of the red triangle is square units. The area of the blue triangle is square units. The area of the green hexagon is square units and the area of the orange hexagon is square units. So, the total area of all the pieces when pulled apart is square units. However, in the first arrangement, they seem to make a triangle with an area of 32.5 square units and in the second arrangement, they seem to have an area of 31.5 square units. The area of these 4 pieces seems to be changing as we are moving them around! What is going on here?

Well, it turns out that neither of the shapes we made using the 4 pieces are in fact triangles. Below is the 1st arrangement. It looks like the red and blue triangles line up perfectly, but they do not. Move the slider below to zoom in on the green line connecting the corners of two triangles.

While the blue and red seem to line up so the ends connect with a straight line, they do not. Using the formula ½ x b x h to find the area of this shape made by the 4 pieces is incorrect because the shape is not is a triangle. The area of this shape is 32 square units. Using 12xbxh, we got 32.5 square units. The extra 12 unit came from the amount of space in between the green line and the actual line connecting the endpoints of the red and blue triangle.

In the 2nd arrangement, the shapes also seem to make a triangle with the same total area, but we’ve used one additional square unit. So, our first thought was that the area of these 4 shapes decreased by one. Move the slider below to zoom in on the green line connecting the corners of two triangles.

Adding the extra square unit into this arrangement of the 4 pieces causes the triangles to bulge outside of the green line. So, this arrangement is not a triangle either! The total area of the pieces is remaining constant at 32!

So, we’ve made sense of this paradox. The area of the green triangle is 32.5 square units and the area of the 4 pieces is 32 square units. The pieces do NOT fit perfectly inside the triangle. When we tried just using the 4 pieces, we still had 12 of a square unit to fill in within the triangle. At first, we just didn’t notice the 12 of the square unit missing.

In the second arrangement, we added in an additional square unit to make the 4 pieces fit inside the green triangle. Again, it seemed to fit, but it actually was 12 square unit too big. Our eyes just couldn’t perceive the extra 12 square unit.

Phew! Our fundamental idea that the area of shapes remains the same regardless of the arrangement of the shapes remains true. We’ll use this idea to explore circles in the next few chapters.