Exercise 10.2
1. From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is ?
Solution:
Let's draw a figure as per the given question.
A tangent at any point of a circle is
Therefore,
By Pythagoras theorem,
r = ±
Radius cannot be a negative value, hence, r =
2. In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°,then ∠PTQ is equal to ?
Solution:
The tangent at any point of a circle is perpendicular to the
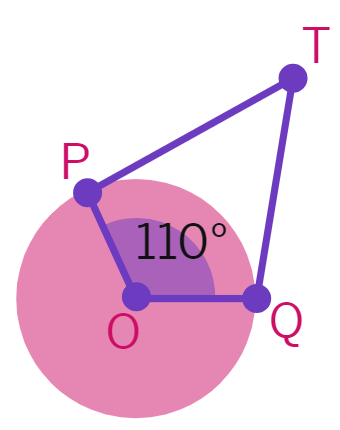
In the above figure,
The sum of the interior angles of a quadrilateral is
Therefore, in OPTQ,
∠Q + ∠P + ∠POQ + ∠PTQ =
∠PTQ = 360° - 290°
∠PTQ =
Therefore, ∠PTQ is equal to 70°.
3. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠POA is equal to ?
Solution:
Let's draw a figure as per the question.
The lengths of tangents drawn from an external point to a circle are
A tangent at any point of a circle is
In ΔOAP and in ΔOBP
OA =
AP =
OP = OP (common)
Therefore, by SSS congruency ΔOAP ≅ Δ
SSS congruence rule: If three sides of one triangle are
If two triangles are congruent then their corresponding parts are
Hence,
∠POA = ∠POB
∠OPA = ∠OPB
Therefore,
Hence, ∠OPA = ∠OPB =
=
=
By angle sum property of a triangle,
In ΔOAP
∠A + ∠POA + ∠OPA =
and OA ⊥ AP.
Theorem : The tangent at any point of a circle is perpendicular to the radius through the point of contact.
Therefore, ∠A =
90° + ∠
130° + ∠POA = 180°
∠POA = 180° -
∠POA =
Therefore,∠POA is equal to 50°.
4. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Solution:
A tangent to a circle is a line that intersects the circle at only
Let's draw the tangents PQ and RS to the circle at the ends of the diameter AB.
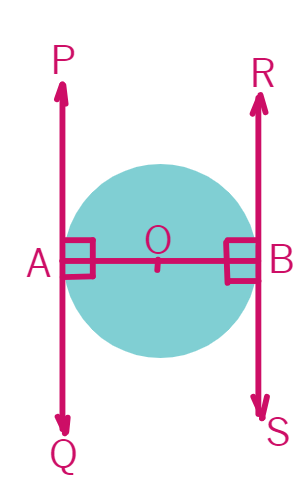
According to theorem: The tangent at any point of a circle is
We know that radius is perpendicular to the tangent at the point of contact.
Thus, OA ⊥
Since the tangents are perpendicular to the
∠PAO = 90°, ∠RBO =
and ∠OAQ =
Here ∠OAQ is equal to ∠
If the alternate interior angles are equal, then lines
We know that
Hence, it is proved that tangents drawn at the ends of a diameter of a circle are parallel.
5. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Solution:
Let's draw a tangent PQ to a circle as shown below.
As we know that, a tangent at any point of a circle is
At the point of contact P,
We also know that the radius or diameter will always pass through the
Therefore,
Hence it is proved that perpendicular PR of tangent PQ passes through centre O.
6. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Solution:
Let's draw a tangent from point A to the circle as shown below.
A tangent at any point of a circle is
Therefore, ∠OTA =
By Pythagoras theorem,
OT = ±
Radius OT cannot be
Hence, the radius is
7. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution:
The chord of the larger circle is a tangent to the smaller circle as shown in the figure below.
PQ is a chord of a larger circle and a tangent of a smaller circle.
Tangent
Therefore, ∠OSP =
In ΔOSP (Right-angled triangle)
By the Pythagoras Theorem,
SP = ±
SP is the length of the tangent and cannot be
Hence, SP =
QS =
Therefore, QS = SP =
Length of the chord PQ = QS + SP = 4 +
PQ =
Therefore, the length of the chord of the larger circle is
8. A quadrilateral ABCD is drawn to circumscribe a circle see below figure. Prove that AB + CD = AD + BC
Solution:
From the given figure we can consider a few points which are as follows:
(i) DR =
(ii) BP =
(iii) AP =
(iv) CR =
Since they are
Now let us add both the LHS and RHS of the above equations separately and observing the result.
DR + BP + AP +
By rearranging the terms we get,
(DR + CR) + (BP +
On further simplifying,
CD +
Hence it is proved AB + CD = AD + BC.
9. In below figure, XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that ∠AOB = 90°.
Solution:
Draw a line between points O and C.
In ΔOPA and ΔOCA
OP =
AP =
AO =
By SSS congruency, ΔOPA ≅ Δ
SSS congruence rule: If three sides of one triangle are equal to the
Therefore, ∠POA = ∠
Similarly, ΔOCB ≅ Δ
Therefore, ∠COB = ∠
PQ is a diameter, hence a straight line and ∠POQ =
But ∠POQ = ∠POA + ∠
∴ ∠POA + ∠AOC + ∠COB + ∠BOQ =
2∠AOC + 2∠COB =
∴ ∠AOC + ∠COB =
From the figure,
∠AOC + ∠COB = ∠
∴ ∠AOB =
Hence, proved ∠AOB = 90°.
10. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Solution:
Let us consider O as the centre point of the circle.
Let P be a point outside the circle from which two tangents PA and PB are drawn to the circle which touches the circle at point
Draw a line segment between points A and B such that it subtends ∠AOB at centre O of the circle.
According to theorem: The tangent at any point of a circle is always perpendicular to the
∴ ∠OAP = ∠OBP =
In a quadrilateral, the sum of interior angles is
∴ In OAPB,
∠OAP + ∠APB + ∠
Using Equation (i), we can write the above equation as
90° + ∠APB +
∠APB + ∠BOA = 360° -
∴ ∠APB + ∠BOA =
Where,
∠APB = Angle between the two tangents
∠BOA = Angle subtended by the line segment
Hence, proved the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
11. Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:
ABCD is a
AB =
BC =
According to theorem: The lengths of tangents drawn from an external point to a circle are equal.
Therefore,
BP =
CR =
DR =
AP =
Adding (1) + (2) + (3) + (4)
BP + CR + DR +
On re-grouping,
BP + AP + CR + DR = BQ + CQ + DS + AS
AB + CD = BC +
Substitute CD = AB and AD = BC since ABCD is a
AB + AB = BC +
2AB =
AB =
∴ AB = BC = CD =
This implies that all the four sides are
Therefore, the parallelogram circumscribing a circle is a rhombus.
12. A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively see below figure. Find the sides AB and AC.
Solution:
Given: Triangle ABC is drawn to circumscribe a circle of radius
From the diagram, BD =
Let, AE = AF = x (The lengths of tangents drawn from an external point to a circle are
CD = CE =
BD = BF =
Using Heron's formula, area of the triangle =
where
s =
a, b and c are sides of a triangle
a = AB = x +
b = BC = 8 + 6 =
c = CA =
s =
s =
s = x +
Area of ΔABC =
=
=
=
Area of ΔABC = Area of Δ
=
= 2x + 12 + 2x + 16 +
= 4x +
=
Equating (1) and (2)
Squaring both sides
48(
48(
3
3
2
Solving by factorization method,
x (x + 14) -
(x + 14)(x -
x + 14 =
x =
Since x represents length, it cannot be
∴ x =
AB = a = x + 8 = 7 + 8 = 15 cm
AC = c = 6 + x = 6 + 7 =
Thus, AB = 15 cm and AC = 13 cm
13. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution:
We know that tangents drawn from a point outside the circle, subtend equal angles at the centre.
In the above figure,
AS =
∠SOA = ∠
Similarly,
∠3 = ∠4, ∠5 = ∠6, ∠7 = ∠
Since complete angle is
We have,
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 =
2 (∠1 + ∠8 + ∠4 + ∠5) = 360° (or) 2 (∠2 + ∠3 + ∠6 + ∠7) =
∠1 + ∠8 + ∠4 + ∠5 =
From above figure,
∠1 + ∠8 = ∠
Thus we have,
∠AOD + ∠BOC = 180° (or) ∠AOB + ∠COD =
∠AOD and ∠BOC are angles subtended by
Hence proved.
