Number of Tangents from a Point on a Circle
In this section let us see the relationship between a point and tangents from the point to the circle.
The point can either be inside, on (or) outside the circle. Let us look at each case one by one.
Case 1: P lies inside the circle
Can you draw a tangent to the circle through this point P? Try to draw a line joining the points O and P.
Conclusion: So, it is not possible to draw any tangent to a circle through a point inside it.
Case 2: P lies on the circle
Can you draw a tangent to the circle through this point P? Try to join the points O and P.
Observation:
Conclusion: Thus,there is only one tangent to the circle at a point located on the circle.
Case 3: P lies outside the circle
Can you draw a tangent to the circle through this point P? Try to join the exterior point A with circle center O.
Observation:
Conclusion: So, exactly two tangents can be drawn to a circle through a point located outside the circle.
Let us consider the third case where T1 and T2 are the points of contact of the tangents PT1 and PT2 respectively.
The length of the segment of the tangent from the external point P and the point of contact with the circle is called the length of the tangent from the point P to the circle.
What can we conclude about PT1 and PT2? As it turns out both
Can we prove that?
Length of tangents from an external point
Theorem: The lengths of tangents drawn from an external point to a circle are equal.
Let's apply the above concepts and check which one has to be applied.
Proof: Given, circle with centre O has a point P outside the circle.
We draw two tangents PR and PQ from the point. We need to prove that PQ = PR
Construction: Join radii OR and OQ. Also join OP. This gives us △OQP and △ORP.
In △OQP and △ORP:
(1) OQ =
(2) OP =
(3) ∠OQP = ∠
Thus, by
△OQP ≅ △
By CPCT:
Hence, the lengths of tangents drawn from an external point to a circle are
Remarks :
1. The theorem can also be proved by using the Pythagoras Theorem as follows:
2. Note also that ∠ OPQ = ∠ OPR. Therefore, OP is the angle bisector of ∠ QPR, i.e., the centre lies on the bisector of the angle between the two tangents.
1. Prove that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
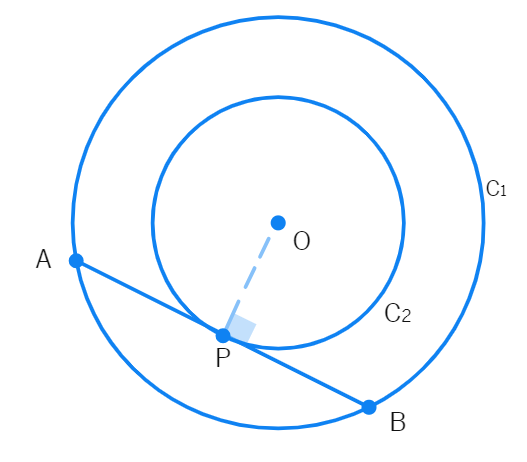
- Let's join OP.Now, AB is a tangent to
C 2 - Now, we know that OP is
to AB. - We also see that AB is a
of the circle C 1 - Therefore, OP is the bisector of the chord AB, as the perpendicular from the centre bisects the chord.
- Hence, AP =
.
2. Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠ PTQ = 2 ∠OPQ.
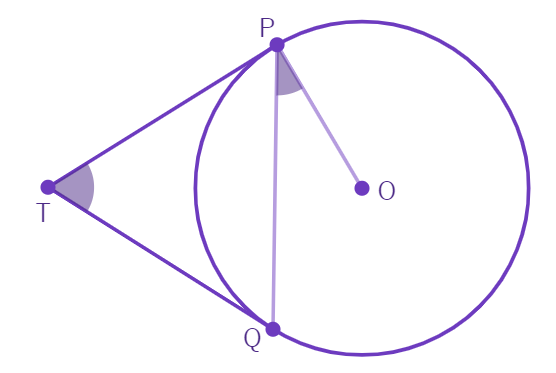
- Let ∠ PTQ = θ. We also know that TP =
. Thus, △TPQ is an triangle - ∠ TPQ = ∠
= 1 2 180 ° − θ ° - θ 2 °) - We also know ∠ OPT =
° - ∠ OPQ = ∠
– ∠ = 90° – ( 90 ° − θ 2 - Hence, ∠ PTQ =
∠ OPQ.
3. PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the length TP.
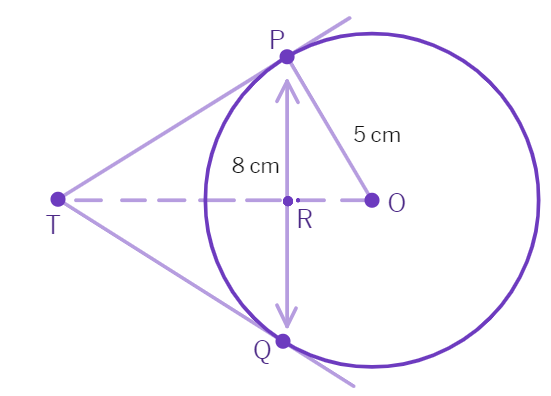
- Join OT and let it intersect PQ at the point R. Also Δ TPQ is
and TO is the angle bisector of ∠ - Thus, OT ⊥
and OT bisects PQ which gives PR = RQ = cm. - OR =
OP 2 − PR 2 5 2 − 4 2 cm. - Now, ∠ TPR + ∠ RPO =
° = ∠ TPR + ∠ PTR - ∠ RPO = ∠
- Therefore, Δ TRP is similar to the Δ PRO by AA similarity. This gives:
TP PO - Putting values: TP =
cm. - Calculating
- Value has been found.
Alternate Method: TP can also be found by using the Pythagoras Theorem, as follows:
Let TP = x and TR = y. Then
Subtracting (1) from (2), we get
y =
=
or x =
