Angle Sum Property of a Triangle
Let's do a simple experiment to find out the angle sum property of a triangle. Can you guess what it is?
Take a piece of paper and cut out a triangle, say, ∆ABC. Make the altitude AM by folding ∆ABC such that it passes through A. Fold the paper triangle such that each vertex/corners A, B and C touches the point M.
Paper triangle ABC
With altitude AM
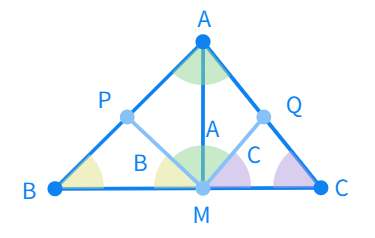
With the obtained fold lines PM and QM.
Another Activity: Draw any number of triangles, say namely ∆ABC, ∆PQR and ∆XYZ. Now, use a protractor and measure each of the angles of all these triangles individually.
| Name of ∆ | Measures of Angles | Sum of the Measures of the three Angles |
|---|---|---|
| ∆ABC | m∠A + m∠B + m∠C = | |
| ∆PQR | m∠P + m∠Q + m∠R = | |
| ∆XYZ | m∠X + m∠Y + m∠Z = |
Allowing some amount of marginal measurement errors, we find that the sum measure of all the three angles for each triangle (last column) always gives 180° (or nearly 180°).
This statement can also be proved using the exterior angle of a triangle property.
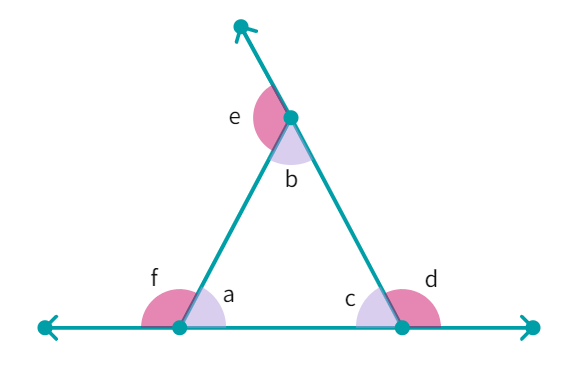
Triangle ABC with exterior angles
- By exterior angle property
- adding
∠ c to both the sides - But ∠c and ∠d form a linear pair so it is 180°.
- RHS =
° and Hence, ∠a + ∠b + ∠c = °.
In the given figure Fig find m∠P.
Fig
Solution:
By angle sum property of a triangle,
m∠P + 47° + 52° =
Therefore
m∠P = 180° –
= 180° – 99° =
1. Two angles of a triangle are 30° and 80°. Find the third angle.
Solution:
Given:
Two angles of the triangle are
To find: The measure of the third angle.
Sum of Interior Angles:
The sum of the interior angles of a triangle is
Angle 1 + Angle 2 + Angle 3 =
Substitute the Known Angles:
Given Angle 1 =
30° + 80° + Angle 3 =
Solve for the Third Angle:
Combine the known angles:
Subtract 110° from both sides:
Angle 3 = 180° -
Angle 3 =
Therefore,The measure of the third angle is 70°.
2. One of the angles of a triangle is 80° and the other two angles are equal. Find the measure of each of the equal angles.
Solution:
Given:
One angle of the triangle is
The other two angles are equal.
To find: The measure of each of the equal angles.
Sum of Interior Angles:
The sum of the interior angles of a triangle is
Angle 1 + Angle 2 + Angle 3 =
Given Information:
Let the equal angles be Angle 1 = Angle 2 = x.
Given Angle 3 =
Set Up the Equation:
Substitute the known values into the sum of angles equation:
x + x +
Combine like terms:
Solve for x:
Subtract 80° from both sides:
2x = 180° -
2x =
Divide both sides by 2:
x =
x =
Therefore,The measure of each of the equal angles is 50°.
3. The three angles of a triangle are in the ratio 1
1. Find all the angles of the triangle.Classify the triangle in two different ways.
Solution:
Given:
The three angles of a triangle are in the ratio
To find: The measure of each angle.
Classify the triangle in two different ways.
Express the Angles in Terms of a Variable:
Let the angles be x, 2x, and x based on the given ratio 11.
Sum of Interior Angles:
The sum of the interior angles of a triangle is 180°.
x + 2x + x =
Combine Like Terms:
Simplify the equation:
Divide both sides by 4: x =
x =
Substitute x = 45°:
First angle = x =
Second angle = 2x = 2 × 45° =
Third angle = x =
Therefore,The three angles are
Classification of the Triangle:
1.By Angles:
Since one of the angles is
2.By Sides:
Since two of the angles are equal (45° each), the triangle is an
isosceles triangle
Therefore, the triangle is classified as both a right-angled triangle and an isosceles triangle.
Property: The total sum of the measures of all the three angles of a triangle is 180°.