Innings2
Create New Account

Sign in to Innings2

or

New Account     Reset Password     

Chapter 6: The Triangles and its Properties

    Introduction

    Medians of a Triangle

    Altitudes of a Triangle

    Comparison and differences between altitudes and medians in a triangle

    Exterior Angle of a Triangle and its Property

    Angle Sum Property of a Triangle

    Two Special Triangles : Equilateral and Isosceles

    Relation between the Lengths of the Sides of a Triangle

    Right-Angled Triangles and Pythagoras Property

    Exercise 6.1

    Exercise 6.2

    Exercise 6.3

    Exercise 6.4

    Exercise 6.5

    What Have We Discussed ?

    Extra Curriculum Support

Powered by Innings 2

Reset Progress

This will delete your progress and chat data for all chapters in this course, and cannot be undone!

Glossary

Select one of the keywords on the left…

Chapter 6: The Triangles and its Properties > Two Special Triangles : Equilateral and Isosceles

Two Special Triangles : Equilateral and Isosceles

In an equilateral triangle:

(i) all sides have length.

(ii) each angle has measure ° ( = 180°3 )

Activity:

Using paper, cut out an isosceles triangle, say XYZ such that XY = XZ. Now fold it so that the Z vertex lies on the Y vertex. The line, say XM through X, is called the axis of symmetry. And we also find that ∠Y and ∠Z fit on each other .

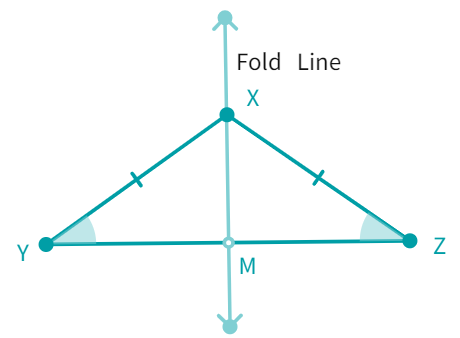
Thus, in an isosceles triangle:

(i) two sides have same length (i.e. XY and XZ are called sides)

(ii) base angles opposite to the equal sides are (YZ is the base while ∠Y and ∠Z are the base angles which are also equal)

Therefore,

A triangle in which all the three sides are of equal lengths is called an triangle.

A triangle in which two sides are of equal lengths is called an triangle.

Instruction

1. Find angle x in each figure:

a

Figure (i)

Solution:

Given angles: ° and x are the base angles of an isosceles triangle.

Since the two base angles are , we get: x = °

Thus, x = 40°.

b

Figure (ii)

Solution:

Given: One angle is 45° and the triangle is .

The other base angle is also °. The sum of angles in a triangle is °:

x + 45° + 45° = 180°

x + ° = 180°

x = 180° - 90° = °

Therefore, x = 90°

c

Figure (iii)

Solution:

Given: One angle is 50° and the triangle is .

The other base angle is also °. The sum of angles in a triangle is °

x + 50° + 50° = 180°

x + ° = 180°

x = ° - ° = °

Therefore, x = 80°

d

Figure (iv)

Solution:

Given: Angles 100° , ∠x and the other ∠x.

Since the two angles are equal-

x + x + 100° = 180°

+ ° = °

2x = °

x = 80°2 = °

Therefore, x = 40°

e

Figure (v)

Solution:

Given: Right angle 90°, ∠x and the other ∠x.

The sum of the angles in a triangle is °.

90° + x + x = 180°

90° + = 180°

2x = °

x = 90°2 = °

Therefore, x = 45°

f

Figure (vi)

Solution:

Given: Angle 40° and the other two angles x and x as the triangle is .

The sum of the angles in a triangle is °

x + x + ° = °

+ 40° = 180°

2x = °

x = 140°2 = °

Therefore, x = 70°

g

Figure (vii)

Solution:

Given: Angle 120° and the other two angles x and x (isosceles triangle).

The sum of the angles in a triangle is 180°

x + x + ° = 180°

+ 120° = 180°

2x = °

x = 60°2 = °

Therefore, x = 30°

h

Figure (viii)

Solution:

Given: Angle 110° and the other two angles x and x (isosceles triangle).

The sum of the angles in a triangle is 180°

x + x + ° = 180°

+ 110° = 180°

2x = °

x = 70°2 = °

Therefore, x = 35°

i

Figure (ix)

Solution:

Given: One exterior angle 30° which is equal to the sum of the two opposite interior angles.

The interior angles are x and x (isosceles triangle).

The sum of the angles in a triangle is 180°

x + x + (° - °) = 180°

2x + ° = 180°

2x = °

x = 30°2 = °

Therefore, x = 15°