Enhanced Curriculum Support

SecA

1. If the angle between two tangents drawn from an external point 𝑃 to a circle of radius 𝑎 and centre 𝑂, is 60°, then find the length of 𝑂𝑃.

2. 𝑃𝑄 is a tangent drawn from an external point 𝑃 to a circle with centre 𝑂, 𝑄𝑂𝑅 is the diameter of the circle. If ∠ 𝑃𝑂𝑅 = 120°, what is the measure of ∠ 𝑂𝑃𝑄?

3. From an external point 𝑃, tangents 𝑃𝐴 and 𝑃𝐵 are drawn to a circle with centre 𝑂. If ∠𝑃𝐴𝐵 = 50°, then find ∠𝐴𝑂𝐵.

4. Two circles touch each other externally at 𝑃. 𝐴𝐵 is a common tangent to the circles touching them at 𝐴 and 𝐵. The value of ∠𝐴𝑃𝐵 is

5. In a right triangle 𝐴𝐵𝐶, right-angled at 𝐵, 𝐵𝐶 = 12 𝑐𝑚 and 𝐴𝐵 = 5 𝑐𝑚. The radius of the circle inscribed in the triangle (in cm) is

6. From a point 𝑄, 13 𝑐𝑚 away from the centre of a circle, the length of tangent 𝑃𝑄 to the circle is 12 𝑐𝑚. The radius of the circle (in 𝑐𝑚) is.

7. A tangent 𝑃𝑄 at a point 𝑃 of a circle of radius 5 𝑐𝑚 meets a line through the centre 𝑂 at a point 𝑄 so that 𝑂𝑄 = 13 𝑐𝑚. Find the length 𝑃𝑄.

8. What is the distance between two parallel tangents of a circle of the radius 4 𝑐𝑚?

9. The length of tangent from a point 𝐴 at a distance of 5 𝑐𝑚 from the centre of the circle is 4 𝑐𝑚. What will be the radius of the circle?

SecB

1. Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.

2. A circle touches all the four sides of a quadrilateral 𝐴𝐵𝐶𝐷. Prove that 𝐴𝐵 + 𝐶𝐷 = 𝐵𝐶 + 𝐷𝐴.

3. Prove that tangents drawn at the ends of a diameter of a circle are parallel to each other.

4. From a point 𝑇 outside a circle of centre 𝑂, tangents 𝑇𝑃 and 𝑇𝑄 are drawn to the circle. Prove that 𝑂𝑇 is the right bisector of line segment 𝑃𝑄.

5. Two concentric circles of radii 𝑎 and 𝑏 (𝑎 > 𝑏) are given. Find the length of the chord of the larger circle which touches the smaller circle.

6. The incircle of an isosceles triangle 𝐴𝐵𝐶, in which 𝐴𝐵 = 𝐴𝐶, touches the sides 𝐵𝐶, 𝐶𝐴 and 𝐴𝐵 at 𝐷, 𝐸 and 𝐹 respectively. Prove that 𝐵𝐷 = 𝐷𝐶.

7. Prove that the parallelogram circumscribing a circle is a rhombus.

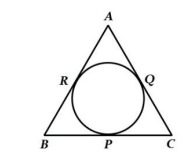
8. Tangents 𝑃𝐴 and 𝑃𝐵 are drawn from an external point 𝑃 to two concentric circles with centre 𝑂 and radii 8 𝑐𝑚 and 5 𝑐𝑚 respectively, as shown in figure. If 𝐴𝑃 = 15 𝑐𝑚, then find the length of 𝐵𝑃.

9. The incircle of an isosceles triangle 𝐴𝐵𝐶, with 𝐴𝐵 = 𝐴𝐶, touches the sides 𝐴𝐵, 𝐵𝐶 and 𝐶𝐴 at 𝐷, 𝐸 and 𝐹 respectively. Prove that 𝐸 bisects 𝐵𝐶.

10. Prove that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.

11. Two concentric circles are of radii 7 𝑐𝑚 and 𝑟 𝑐𝑚 respectively, where 𝑟 > 7. A chord of the larger circle, of length 48 𝑐𝑚, touches the smaller circle. Find the value of 𝑟.

12. Two tangents 𝑃𝐴 and 𝑃𝐵 are drawn to a circle with centre 𝑂 from an external point 𝑃. Prove that ∠𝐴𝑃𝐵 = 2∠𝑂𝐴𝐵.

SecC

1. The incircle of Δ𝐴𝐵𝐶 touches the sides 𝐵𝐶, 𝐶𝐴 and 𝐴𝐵 at 𝐷, 𝐸, and 𝐹 respectively. If 𝐴𝐵 = 𝐴𝐶, prove that BD = CD

2. Prove that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at the centre of the circle.

3. Prove that the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

4. Two tangents 𝑇𝑃 and 𝑇𝑄 are drawn to a circle with centre 𝑂 from an external point 𝑇. Prove that ∠ 𝑃𝑇𝑄 = 2 ∠ 𝑂𝑃𝑄.

5. 𝑃 & 𝑄 are centres of circles of radii 9 𝑐𝑚 and 2 𝑐𝑚 respectively. 𝑃𝑄 = 17 𝑐𝑚. 𝑅 is the centre of the circle of radius 𝑥 𝑐𝑚 which touches the above circle externally. Given that angle 𝑃𝑅𝑄 is 90°. Write an equation in 𝑥 and solve it.

6. Two tangents 𝑇𝑃 and 𝑇𝑄 are drawn to a circle with centre 𝑂 from an external point 𝑇. Prove that ∠𝑃𝑇𝑄 = 2 ∠𝑂𝑃𝑄.

7. Prove that the parallelogram circumscribing a circle is a rhombus.

8. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

SecD

1. Prove that the lengths of two tangents drawn from an external point to a circle are equal.

2. The radii of two concentric circles are 13 𝑐𝑚 and 8 𝑐𝑚. 𝐴𝐵 is a diameter of the bigger circle and 𝐵𝐷 is tangent to the smaller circle touching it at 𝐷 and intersecting the larger circle at 𝑃, on producing. Find the length of 𝐴𝑃.

3. Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.

4. Prove that the lengths of the tangents drawn from an external point to a circle are equal. Using the above theorem, prove that 𝐴𝐵 + 𝐶𝐷 = 𝐴𝐷 + 𝐵𝐶, if a quadrilateral 𝐴𝐵𝐶𝐷 is drawn to circumscribe a circle.

5. Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.

6. Prove that the lengths of the tangents drawn from an external point to a circle are equal.

7. Prove that the tangent drawn at the mid–point of an arc of a circle is parallel to the chord joining the end points of the arc.

8. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

9. A quadrilateral 𝐴𝐵𝐶𝐷 is drawn to circumscribe a circle. Prove that 𝐴𝐵 + 𝐷𝐶 = 𝐴𝐷 + 𝐵𝐶.

10. Prove that the lengths of the tangents drawn from an external point to a circle are equal. Using the above theorem prove that: If quadrilateral 𝐴𝐵𝐶𝐷 is circumscribing a circle, then 𝐴𝐵 + 𝐶𝐷 = 𝐴𝐷 +𝐵�_

11. Prove that the lengths of tangents drawn from an external point to a circle are equal. Using the above, prove the following: 𝐴𝐵𝐶 is an isosceles triangle in which 𝐴𝐵 = 𝐴𝐶, circumscribed about a circle, as shown in Fig. Prove that the base is bisected by the point of contact.

Problem1

Situation: A park is designed with a circular pathway around a fountain. The radius of the circular pathway is 20 meters. The park authorities want to install benches at regular intervals along the circumference of the pathway to allow visitors to rest.

1. Calculate the total circumference of the circular pathway. If a bench is placed every 5 meters, how many benches are needed?

2. Why is it important to design public spaces with resting points, and how does geometry help in making such calculations?

Problem2

Situation: The school’s circular playground has a radius of 50 meters. A flagpole is erected at the center of the playground, and two students stand on the circumference of the playground at points A and B. The distance between them along the circle’s circumference is 75 meters.

1. Find the angle subtended by the arc AB at the center of the playground.

2. Discuss the importance of understanding geometric shapes like circles in architectural and landscaping designs.

Problem3

Situation: A farmer has a circular field with a radius of 30 meters. He installs a sprinkler at the center of the field, which sprays water up to a radius of 15 meters.

1. Calculate the area of the field that will remain dry.

2. How do circles and areas help in solving practical problems like irrigation in agriculture?

Problem4

Situation: A historical monument has a circular base with a radius of 25 meters. The authorities want to install a protective fence 2 meters away from the edge of the monument, forming another concentric circle around it.

1. Calculate the area between the two circles that will be enclosed by the fence.

2. Why is it important to protect historical monuments, and how do geometrical concepts aid in preservation efforts?

Problem5

Situation: A round table conference is arranged in a hall where the table has a radius of 2 meters. Ten people are seated equally spaced along the circumference of the table.

1. Calculate the angle subtended at the center of the table by each pair of adjacent participants.

2. How does arranging people in a circular formation help in promoting equal participation, and what is the importance of symmetry in real-life arrangements?

Q1

From an external point P, two tangents PA and PB are drawn to a circle with center O. The length of the tangents is 12 cm, and the distance from P to the center O is 13 cm.

1. Find the radius of the circle and prove that the tangents drawn from an external point are equal.

Q2

A circle is inscribed in a triangle ABC. The tangents drawn from a point P on the circumcircle of the triangle to the inscribed circle touch it at points Q and R. The length of PQ is equal to PR.

1. Prove that the line through Q and R is parallel to one of the sides of the triangle.

Q3

In a cyclic quadrilateral ABCD, where AB = 9 cm, BC = 7 cm, CD = 6 cm, and DA = 8 cm, the diagonals AC and BD intersect at right angles.

1. Prove that the sum of the opposite angles of the quadrilateral is 180°, and find the radius of the circumcircle of the quadrilateral.

Q4

Two circles with radii 5 cm and 7 cm are externally tangent to each other. The distance between the centers of the circles is 15 cm.

1. Find the length of the direct common tangent between the two circles, and explain the significance of this tangent in real-world situations.

Q5

In a circle with center O, a chord AB subtends an angle of 60° at the center. A point P lies on the major arc of the circle such that the angle subtended by the chord at point P is 45°.

1. Find the radius of the circle and prove that the angle subtended by a chord at any point on the major arc is always less than the angle subtended at the center.

Q6

Two circles intersect at points A and B. A line passing through point A meets the circles again at points C and D, respectively.

1. Prove that BC = BD and explain the relationship between the intersecting circles and the common chord.

Questions

1. If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = a√2.

2. From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is

3. At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XT and at a distance 8 cm from A is

4. If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then length of each tangent is equal to

5. Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.

6. Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.

7. If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.

8. Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F respectively, prove that BD = s – b.

9. From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the perimeter of the triangle PCD.

10. Two circles with centres O and O’ of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O’P are tangents to the two circles. Find the length of the common chord PQ.

11. In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC at P. Prove that the tangent to the circle at P bisects BC.

12. AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°.The tangent at C intersects extended AB at a point D. Prove that BC = BD.

13. The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, Find ∠CBA.

14. if an isosceles triangle ABC, in which AB = AC = 6 cm, is inscribed in a circle of radius 9 cm, find the area of the triangle.

15. 1 is a point at a distance 13 cm from the centre 0 of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.

16. If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.

Question 1

Ramesh was fond of spinning / revolving a ball tied with a rope. While playing, the ball slipped from the rope and hit to his brother Suresh playing nearby. Suresh threw the ball back to Ramesh that made an angle with the path AX but the ball followed the path presented by XYZ which touches the imaginary circumference of the circle.

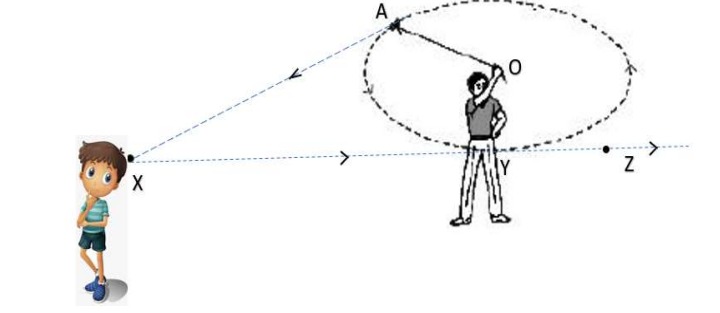
Based on your understanding of the above case study, answer all the five questions below

1. If the length of the rope used by Ramesh is 2 meters, then the distance from O to X is

2. The path represented by AX is

3. The length of XY is

4. Suresh & Ramesh are called by their parent to know what happened exactly while playing. Ramesh explained the incident. Suresh also gave his opinion. Finally, it is decided that Suresh will be asked a question and he needs to give the correct answer.

Suresh father told him to bring the rope that he used while playing. He is asked to make a circle using that rope. The radius of the circle so obtained is

5. If the length of the sides of the container AB, BC & AD are 3feet, 5 feet & 5 feet respectively, then the length of the lid represented by CD is

Question 2

Due to the COVID pandemic, no schools are opened. Arpita was at home for last 7 months. She gained 10kg weight during this period. So, her father decided to purchase a bicycle as he knows that cycling is a very good exercise. She was presented a new bicycle and she was very happy. She found that there were no mud guards in the cycle. She told her father to attach two mud guards. One at the front and another at the back.Her father attached mud guards and two circular protectors of the wheels She observed that while pedaling, chain and the chain wheels rotate simultaneously. When the bigger chain wheel completes one rotation, the smaller completes two rotations.The two chain wheels are 1 meter away from their centers.

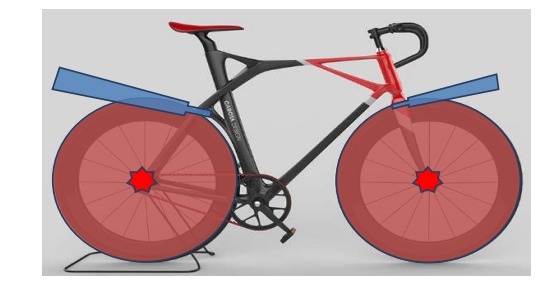
Based on your understanding of the above case study, answer all the five questions below:

1. If the diameter of the bigger chain wheel is 20cm, then the radius of the smaller chain wheel is

2. If the radius of the circular protector is 18cm and the length of the mud-guard is 24cm, then the distance from X to Z is

3. Let’s assume the mud guard of the front wheel just touches the wheel, the mud guard represents

4. A football is packed in the box in such a way that the ball touches all faces of the box. Which of the following is not true?

5. The front view of the box looks like the following, if AB, BC & CD are x units, y units & z units respectively, then AD represented by