Innings2
Create New Account

Sign in to Innings2

or

New Account     Reset Password     

Chapter 12: Applications of Trigonometry

    Introduction

    Drawing Figures to Solve Problems

    Solution for Two Triangles

    Summary

    Enhanced Curriculum Support

    Easy Level Worksheet

    Moderate Level Worksheet

    Hard Level Worksheet

Powered by Innings 2

Reset Progress

This will delete your progress and chat data for all chapters in this course, and cannot be undone!

Glossary

Select one of the keywords on the left…

Chapter 12: Applications of Trigonometry > Introduction

Introduction

In the previous chapter, we have studied about trigonometric ratios. In this chapter, we will be looking at some ways in which trigonometry is used in the life around you.

Looking at a tower

Say we are looking at the top of a tower. From our eye level a line can be drawn to the top of the tower which is called the line of sight. This line of sight makes an angle with the horizontal, which is called the angle of elevation of the top of the tower from the eye of the observer i.e. when we raise our head to look at the object.

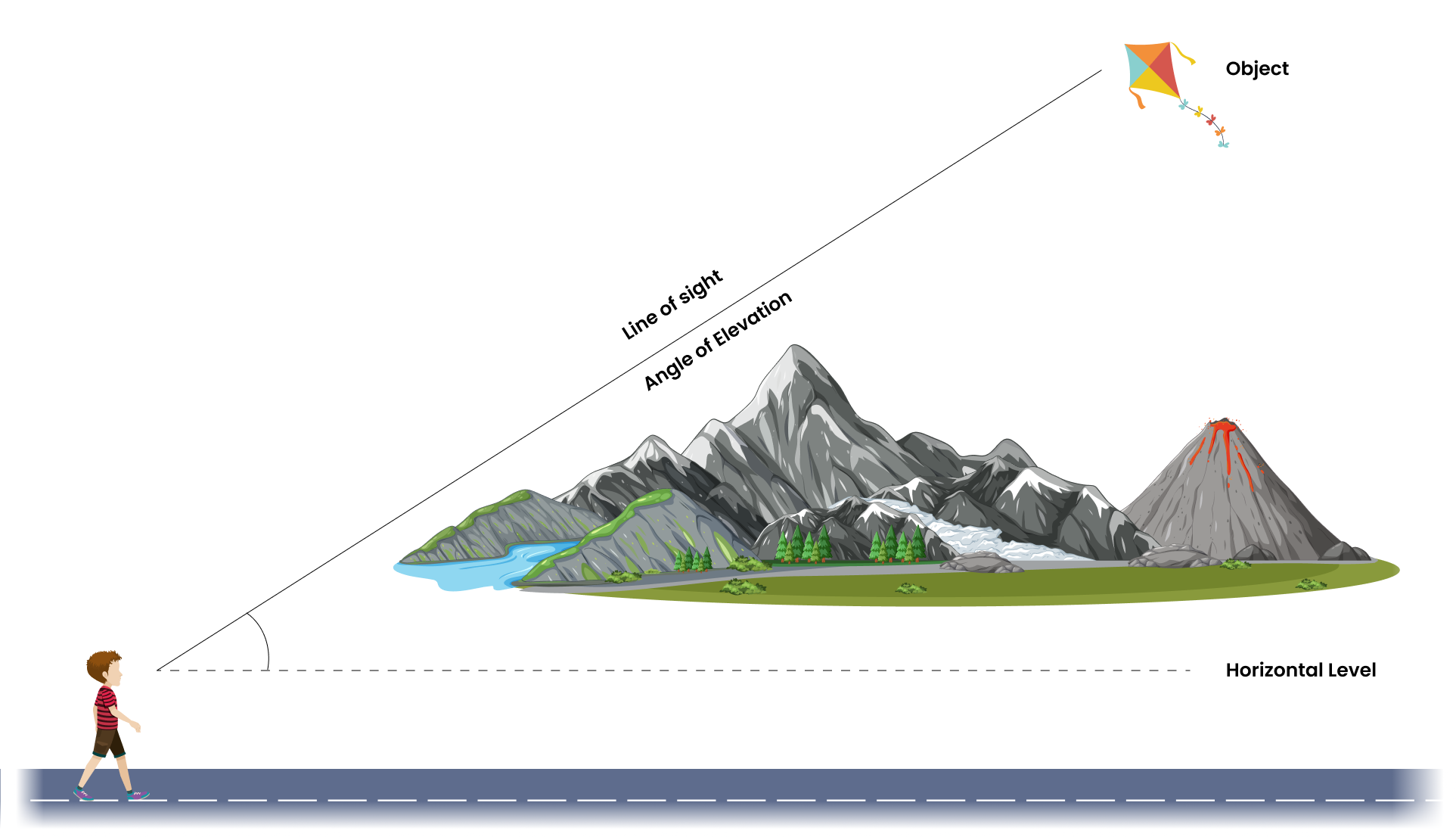
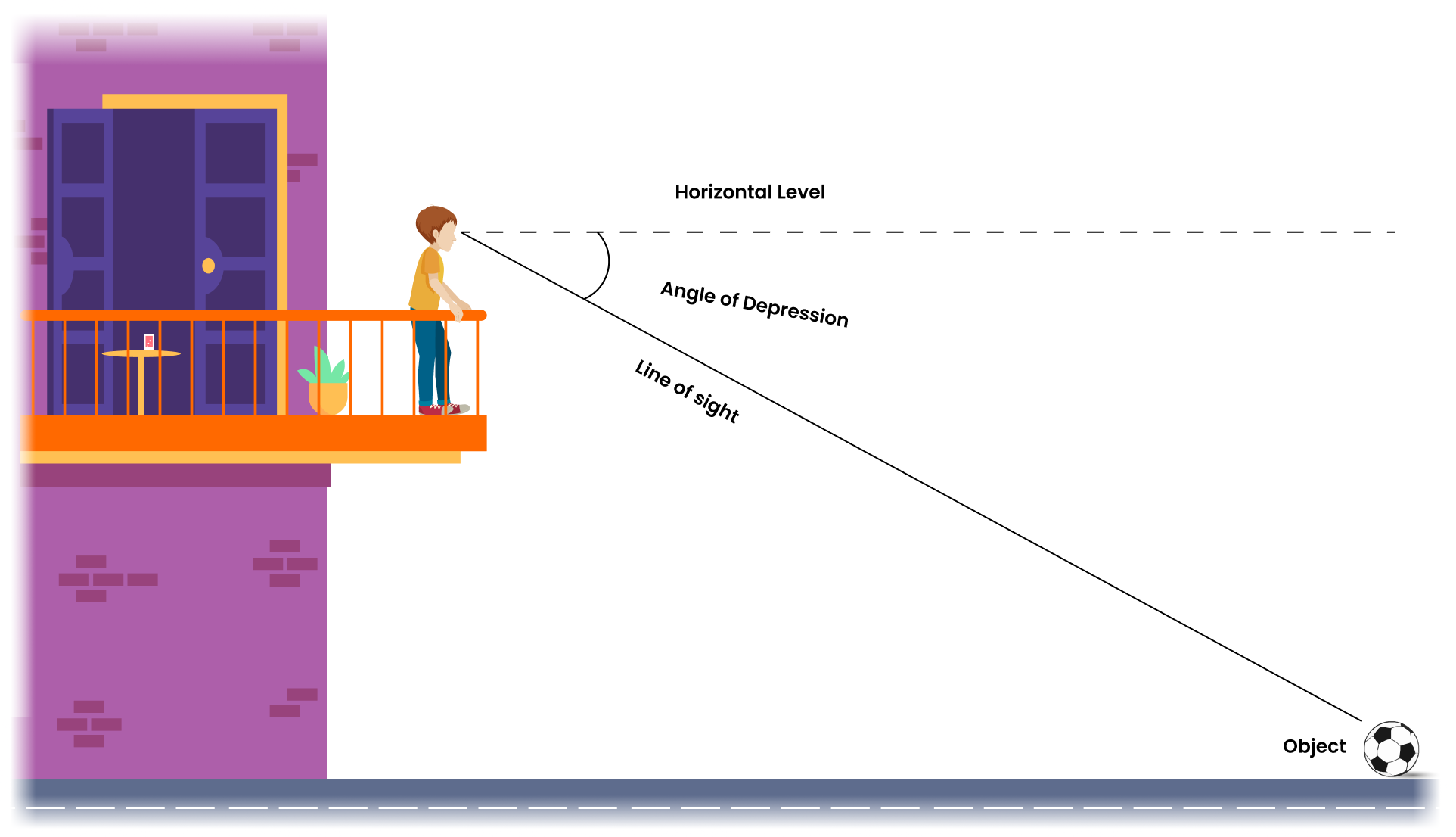
Now, look at the reverse case. Say, somebody is looking at us from the top of the tower In this case, the line of

sight (drawn from the eye of the observer) is below the reference line.

The angle so formed by the line of sight with the horizontal is called the angle of depression.

Thus, the angle of depression of a point on the object being viewed is the angle formed by the line of sight with the horizontal when the point is below the horizontal level, i.e., the case when the observer lowers their head to look at the point being viewed.

Now, let's look at the figure given below.

A person is looking at the top of the hill from the ground level and another person is watching the ground from the top of the hill.

Can you identify the lines of sight, and the angles so formed in the figure?

What are the angles of elevation (or) angles of depression?

Angle of elevation : Angle of depression : Line of Sight :

In this figure, the line AB drawn from the eye of A to the top of the mountain is called the line of sight. A is looking at the top of the mountain. ∠CAB is called the of the top of the mountain from the eye of the student.

Now, consider the situation of B. B is standing on the moutain and looking down at A. In this case, the line of sight is the horizontal level. ∠ABC is called the .

If we want to find the height of the mountain i.e. line BC without actually measuring it, what information do we need? We would need to know the following:

(i) the distance AC at which the ground observer is standing from the foot of the mountain

(ii) the angle of elevation: ∠ CAB of the top of the mountain

(iii) the height of the ground observer (AE).

We need the height of observer because we need to add that as the triangle is formed only till the horizontal level.

Assuming that the above three conditions are known, can we determine the height of the mountain?

Given that we know the distance AC and the angle: the trigonometric ratio that can be used to find the height is .

So, the height of the mountain is :

tanangle of elevation x Distance of A from the mountain + height of A