Centroid Triangle

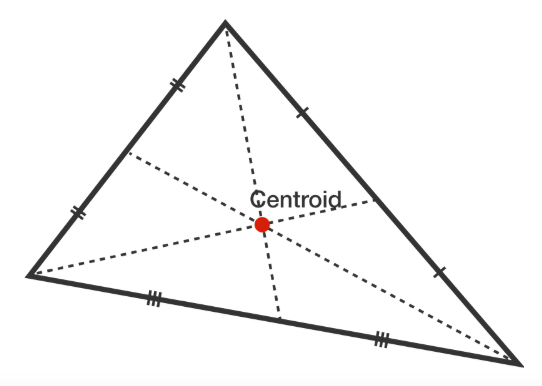
We know:

The is the point where all three medians of a triangle intersect.

A connects a vertex to the midpoint of the opposite side.

The centroid divides each median in the ratio from the vertex.

How do we get this?

Given: Let triangle ABC have vertices at: A(x1, y1), B(x2, y2), and C(x3, y3)

Step 1: Find the Midpoint of Side BC

The median from vertex goes to the midpoint of the opposite side BC.

Let's call this midpoint D. Using the midpoint formula: D = ( x2+x32x1+x22, y2+y32y1+y32 )

Step 2: Apply the Key Property of Centroids

The centroid G lies ondoesn't lie on the median AD and divides it internally in the ratio from the vertex A.

This means: AG : GD = 2 : 1

In other words, G divides the line segment joining A and D in the ratio 2:1.

Step 3: Apply the Section Formula

When a point divides a line segment joining two points internally in a given ratio, we use the section formula.

For a point dividing the line joining A(x1, y1) and D(x2+x32, y2+y32) in the ratio 2

G = (m·x2+n·x1m+n, m·y2+n·y1m+n)

where m = , n = , and the second point coordinates are from D.

Step 4: Calculate the x-coordinate of G

x-coordinate of G = 2×x2+x32+1×x12+1 = x2+x3+x13x2+x3+x13 = x1+x2+x33x1−x2−x33

Step 5: Calculate the y-coordinate of G

y-coordinate of G = 2×y2+y32+1×y12+1 = y2+y3+y13y2+y3+y13 = y1+y2+y33y1−y2−y33

Therefore, the centroid of a triangle with vertices A(x1, y1), B(x2, y2), and C(x3, y3) is:

G = (x1+x2+x33, y1+y2+y33)

Example 1: Find the centroid of a triangle with vertices at A(1, 4), B(5, -2), and C(-3, 8).

Solution: Using the centroid formula:

x-coordinate: 1+5+−33 = 33−63 =

y-coordinate: 4+−2+83 = 10373

Therefore, the centroid is at G(1, 103).

Example 2: Find the ratio in which the point (2, 1) divides the line segment joining A(-1, 3) and B(8, -3).

Solution:

Let the ratio be m:n. Using the section formula:

For x-coordinate: 2 = 8m+−1nm+n

2m+n2mn = 8m−n8m+n

2m + 2n = 8m - n

n = m

mn =

Therefore m:n = 1:2

Verification with y-coordinate: 1 = −3m+3nm+n

With m = 1, n = 2: −31+321+2 =

The ratio is 1:2. So, we have verified the result!

Example 3: Find the ratio in which the x-axis divides the line segment joining points A(3, 8) and B(-5, -4). Also find the point of intersection.

Solution:

Let the ratio be k:1. The point on the x-axis has y-coordinate = .

Using section formula for y-coordinate:

= k−4+18k+1 ⇒ 0 = + 8 ⇒ 4k = 8 ⇒ k =

So the ratio is 2:1.

Finding the intersection point using x-coordinate: x = 2−5+132+1 =

The point of intersection is (−73, 0).

Example 4: Show that the points P(2, 1), Q(5, 4), R(8, 3), and S(5, 0) form a parallelogram.

Solution: For a parallelogram, the midpoints of diagonals PR and QS must be the samehaving the same x-coordinatehaving the same y-coordinate.

Midpoint of PR = (2+82, 1+32) = (, ) (Enter fraction forms) = (, )

Midpoint of QS = (5+52, 4+02) = (, ) (Enter fraction forms) = (, )

Since both midpoints are equal, PQRS is a parallelogram.

Example 5: If A(4, 2), B(7, 5), C(10, 6), and D(q, r) are vertices of a parallelogram, find the values of q and r.

Solution: The midpoint of AC will be the same as the midpoint of .

Midpoint of AC = (4+102, 2+62) = (, )

Midpoint of BD = (7+q25+r2, 5+r27+q2)

Equating: 7+q2 = 7 ⇒ 7 + q = ⇒ q =

5+r2 = 4 ⇒ 5 + r = ⇒ r =

Therefore, D(7, 3).