TriSectional Points of a Line

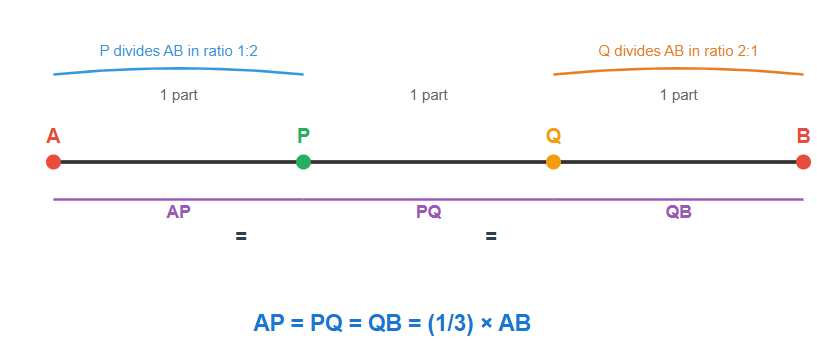
The points which divide a line segment into three equal parts are called trisectional points.

When a line segment is divided by two points into three equal segments, these dividing points are known as points of trisection. If we have a line segment AB with trisectional points P and Q, then AP = PQ = QB.

Finding Trisectional Points Using Section Formula

To find the coordinates of trisectional points, we apply the section formula twice:

(1) The first trisectional point divides the line segment in the ratio 1:22:1.

(2) The second trisectional point divides the line segment in the ratio 2:11:2.

Let's try it out with a problem:

Find the coordinates of the points of trisection of the line segment joining the points A(2, −2) and B(−7, 4).

Solution:

Let P and Q be the points of trisection of line segment AB, such that AP = PQ = QB.

Step 1: Finding point P

Point P divides AB internally in the ratio 1:2.

Using the section formula:

P(x, y) = (m1x2+m2x1m1+m2,m1y2+m2y1m1+m2)

Where m1 = , m2 = while A(2, −2) = (x1, y1), and B(−7, 4) = (x2, y2)

P(x, y) = (1−7+221+2, 14+2−21+2)

P(x, y) = (−7+43, 4−43) = (−33−13, 0363) = (, )

Step 2: Finding point Q

Point Q divides AB internally in the ratio :.

Q(x, y) = (2−7+122+1, 24+1−22+1)

Q(x, y) = (−14+23, 8−23) = (−123123, 6393) = (, )

Thus, the coordinates of the points of trisection are P(−1, 0) and Q(−4, 2).

8. Find the coordinates of the points of trisection (i.e., points dividing in three equal parts) of the line segment joining the points A(2, – 2) and B(– 7, 4) (Given in the above figure).

Solution : Let P and Q be the points of trisection of AB i.e., AP = PQAB = QB

Therefore, P divides AB internally in the ratio 1 : 2.

Therefore, the coordinates of P, by applying the section formula, are:

(1−7+221+2 , 14+2−21+2) = (Put comma in between the two numbers)

Now, Q also divides AB internally in the ratio 2 : 1. So, the coordinates of Q are:

(2−7+121+2 , 24+1−21+2) = (Put comma in between the two numbers)

Therefore, the coordinates of the points of trisection of the line segment joining A and B are (–1, 0) and (– 4, 2).

Note : We could also have obtained Q by noting that it is the mid-point of PB. So, we could have obtained its coordinates using the mid-point formula.

9. Find the ratio in which the y-axis divides the line segment joining the points (5, – 6) and (–1, – 4). Also find the point of intersection.

Solution : Let the ratio be k : 1. Then by the section formula, the coordinates of the point which divides AB in the ratio k : 1 are

(−k+5k+1, −4k−6k+1)

This point lies on the y-axis, and we know that on the y-axis the abscissa is .

Therefore, −k+5k+1 = 0

This gives us k =

That is, the ratio is : .

Putting the value of k = 5, we get the point of intersection as (0, −133)(0,−83)(0,−113).

10. If the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a parallelogram, taken in order, find the value of p.

Solution : We know that diagonals of a parallelogram bisectperpendicular each other.

So, the coordinates of the mid-point of AC = coordinates of the mid-point of BD

(6+92, 1+42) = (8+p2, 2+32)

(, ) = (8+p2, 52)

152 = 8+p2

p =