Measuring of an Angles

In the previous section, we made a tester to help classify angles into the different categories. But as always, apart from the general classification, values are required when dealing with these basic concepts in the real-life scenario.

In order to be more precise in comparison, we need to ‘measure’ the angles and that can be done with the help of a ‘protractor’.

An unit of angle is a degree. A degree, symbolized as "°", is a unit of measurement for angles. One degree represents 1360° of a full circular rotation. So, a complete circle is divided into °.

Think discuss and write

How many degrees are there in full a revolution? A full rotation is ° while one straight angle is ° and a quarter rotation is °, and so on.

Let's continue to measuring angles. Continue

Paper Tester for Measuring Angles

Similar to what we did in the previous section to classify angles using the "right-angle-tester" , we will do something similar to narrow down the range in which a said angle's value may lie.

Take a circular paper (or) cut out a circle from a large enough piece of paper using a bangle.

Now, fold the circle cut out along its diameter (say AB in figure) and then fold the resulting semi-circle again in half (say OC in figure). It becomes a quadrant upon doing so.

Open it out. You will find a semi-circle with a fold in the middle. Mark 90^o on the fold (at point C in figure).

Now further, fold the quadrant once more in half. The angle becomes half of ^o i.e. ^o. (at point D in figure)

Upon opening the folds (keep it folded as a semi-circle), two more folds appear on each side. (OD, OE, OF, OG in figure)

From the point B, the point E is half the angle of OD i.e. half of ° i.e. 22 ^o.

Point F corresponds to point D but since the angle is being measured from point B, it becomes 90^o + 45^o = ^o.

Similarly, point G is 22 ^o more than point F , so it becomes 135 ^o + 22 ^o = ^o.

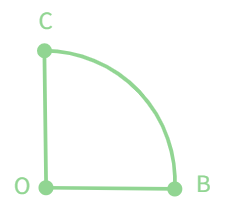
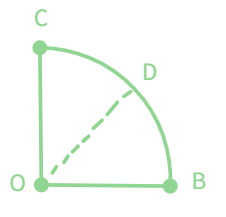
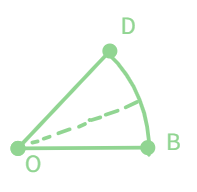
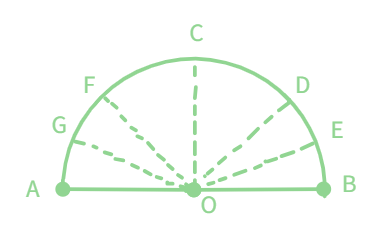
Now, we have a do-it-yourself protractor which will help us get a rough idea about the range of the angle being measured.

Protractor

Protractor

Protractor

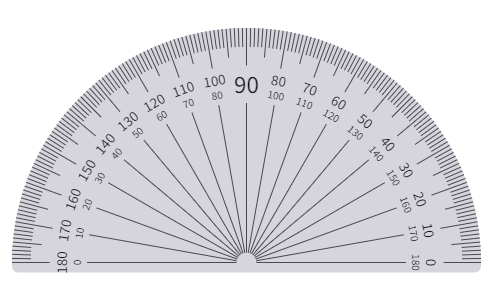
The curved edge of a protractor is divided into 180 equal parts. Each part is equal to a ‘degree’. The markings start from 0° on the right side and ends with 180° on the left side, and vice-versa.

Continue

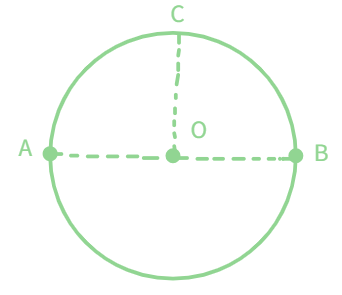
Now, take an angle AOB, as shown below

In order to measure a given angle:

• Place the protractor so that the mid point of its straight edge lies on the vertex O of the angle.

• Adjust the protractor so that OA is along the straight-edge of the protractor.

• There are two ‘scales’ on the protractor : read that scale which has the 0° mark coinciding with the straight-edge i.e. OA.

• The mark on the curved edge gives the degree measure of the angle at the point where the angle arm OB coincides with the corresponding marking.

Let's Solve

1. Draw the angle for the given measure angles by using protractor like in the below figure:

(i) Draw an angle named ∠AOB with the angle measure = 90°

(ii) Draw an angle named ∠AOC with the angle measure = 135°

(iii) Draw an angle named ∠DOB with the angle measure = 180°