Direct Proportion

If the cost of 1 kg of sugar is ₹ 36, then what would be the cost of 3 kg sugar?

It is ₹ .

Similarly, we can find the cost of 5 kg or 8 kg of sugar. Study the following table.

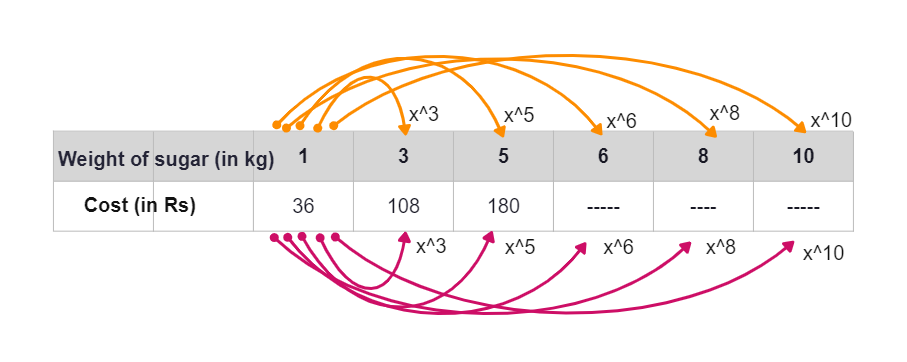
Observe that as weight of sugar increases, cost also increases in such a manner that their ratio remains .

Take one more example.

Suppose a car uses 4 litres of petrol to travel a distance of 60 km.

How far will it travel using 12 litres?

The answer is 180 km.

How did we calculate it?

Since petrol consumed in the second instance is 12 litres, i.e., three times of 4 litres, the distance travelled will also be three times of 60 km. In other words, when the petrol consumption becomes three-fold, the distance travelled is also three fold the previous one. Let the consumption of petrol be x litres and the corresponding distance travelled be y km .

Now, complete the following table:

Petrol in litres (x)	Distance in km (y)
4	60
8
12	180
15
20
25

Instructions

We find that as the value of x increases, value of y in such a way that the ratio xy does not change; it remains constant (say k). In this case, it is 115 (check it!).

We say that x and y are in direct proportion, if xy = k or x = ky.

In This Example: 460 = 12180 where 4 and 12 are the quantities of petrol consumed in litres (x) and 60 and 180 are the distances (y) in km. So when x and y are in direct proportion.

we can write x1y1 = x2y2. (y1, y2 are values of y corresponding to the values x1,x2 of x respectively)

The consumption of petrol and the distance travelled by a car is a case of direct proportion. Similarly, the total amount spent and the number of articles purchased is also an example of proportion.

Thus, variables increasing (or decreasing) together need not always be in direct proportion.

For Example:

(i) physical changes in human beings occur with time but not necessarily in a predetermined ratio.

(ii) changes in weight and height among individuals are not in any known proportion and

(iii) there is no direct relationship or ratio between the height of a tree and the number of leaves growing on its branches. Think of some more similar examples.

(i) Take a clock and fix its minute hand at 12.

Record the angle turned through by the minute hand from its original position and the time that has passed, in the following table:

Angle per minutes = 36060 = °

The angles turned after T minutes is : Angle turned(A) = 6 x T.

Time passed(T)(in minutes)	(T1)15	(T2)	(T3)	(T4)
Angles turned(A) (in degree)	(A190)	(A2)	(A3)	(A4)
TA

What do you observe about T and A?

Do they increase together?

, as T increases, A also increases proportionally.

Is TA same every time?

, TA = 16 remains constant for all intervals.

Is the angle turned through by the minute hand directly proportional to the time that has passed?

Yes! , A ∝ T as the angle turned is directly proportional to the time passed.

From the above table, you can also see

T1 : T2 = A1 : A2, because

T1 : T2 = 15 : 30 = 1 : 2

A1 : A2 = 90 : 180 = 1 : 2

T2 : T3 = A2 : A3 = 30 : 45 = 180 : 270 = :

T3 : T4 = A3 : A4 = 45 : 60 = 270 : 360 = :

You can repeat this activity by choosing your own time interval.

(ii) Ask your friend to fill the following table and find the ratio of his age to the corresponding age of his mother.

Let's try with an example friend's present age(F) is 15 years , Mother's present age (M) is 40 years.

	Age five years ago	Present age	Age after five years
Friend's age(F)	15 - 5 =		15 + 5 =
Mothers's age(M)	40 - 5 =		40 + 5 =
FM	1035 =	1540 =	2045 =

What do you observe?

Do F and M increase (or decrease) together?

, as time progresses, both F and M increase by the same number of years (5 years).

Is FM same every time?

No! , the ratio FM changes as time progresses because the friend’s age grows faster relative to their mother’s age.

You can repeat this activity with other friends and write down your observations.

1. Observe the following tables and find if x and y are directly proportional.

x	y
20	40
17	34
14	28
11	22
8	16
5	10
2	4

Instructions

2040 = , and 1734 =,

1428=, and 1122 = ,

816 = , and 510 = , and 24 =

Hence, x and y are .

(ii)

x	y
6	4
10	8
14	12
18	16
22	20
26	24
30	28

64 = , and 108 =,

1412=, and 1816 = ,

2220 = , and 2624 = , and 3028 =

Hence, x and y are .

(iii)

x	y
5	15
8	24
12	36
15	60
18	72
20	100

515 = , and 824 =,

1236 = , and 1560 =,

1872 = , and 20100 =,

Hence, x and y are .

2. Principal = Rs. 1000, Rate = 8% per annum. Fill in the following table and find which type of interest (simple or compound) changes in direct proportion with time period.

Time Period	1 year	2 year	3 year
Simple Interest (in Rs.)
Compound Interest (in Rs.)

Solution:

Time Period	1 year	2 year	3 year
Simple Interest (in Rs.)
Compound Interest (in Rs.)

If we fix time period and the rate of interest, simple interest changes proportionally with principal. Would there be a similar relationship for compound interest? Why?

If we fix the time period and the rate of interest, compound interest also changes proportionally with the principal.

In both cases, when P changes, the interest (both simple and compound) changes proportionally. This is because compound interest, for a fixed time and rate, is essentially a scaled-up value based on the principal, much like simple interest, except with a compounded growth factor applied.

Thus, compound interest is directly proportional to the principal when time and rate are held constant.

The cost of 5 metres of a particular quality of cloth is ₹ 210. Tabulate the cost of 2, 4, 10 and 13 metres of cloth of the same type.

Solution

Suppose the length of cloth is x metres and its cost, in ₹ , is y.

x (in ₹ )	y
2	y2
4	y3
5	210
10	y4
13	y5

As the length of cloth increases, cost of the cloth also increases in the same ratio. It is a case of direct proportion.

(i) Here x1 = 5, y1 = 210 and x2 = 2

x1y1=x2y2

Here, x1y1= x2y2 gives
or 5y2 =
or y2=
Therefore,the result is 84.

(ii) If x3 = 4, then 5210 = 4y3

5210=4y3

Here, x3 = 4
So, y3 =
Therefore, the result is 168.

(iii) If x4 = 10, then 5210=10y4 or

5210=10y4

Here, x4 = 10
So, y4 =
Therefore, the result is 420.

(iv) If x5 = 13, then 5210=13y5 or

5210=13y5

Here, x5 = 13
So, y5 =
Therefore, the result is 546.

An electric pole, 14 metres high, casts a shadow of 10 metres. Find the height of a tree that casts a shadow of 15 metres under similar conditions.

Let the height of the tree be x metres.We form a table as shown below:

Height of the object (in metres)	14	x
Length of the shadow (in metres)	10	15

Note that more the height of an object, the more would be the length of its shadow. Hence, this is a case of direct proportion.

x1y1 = x2y2

We have 1410 = x15

x = 14×1510 = m

Thus, height of the tree is 21 metres.

Alternately, we can write: x1y1 = x2y2 as x1x2 = y1y2

x1:x2 = y1:y2

(or) : x = : 15

Therefore, 10 × x = 15 × 14

or x = 14×1510 =

If the weight of 12 sheets of thick paper is 40 grams, how many sheets of the same paper would weigh 212 kilograms?

Solution:

Let the number of sheets which weigh 212 kg be x. We put the above information in the form of a table as shown below:

Number of sheets	Weight of sheets (in grams)
12	40
x	2500

Finding number of sheets

1 kilogram = grams
212 = grams
So, 1240 = x2500
Therefore x =
Thus, the required number of sheets of paper = 750

Alternate method:

Two quantities x and y which vary in direct proportion have the relation x = ky or xy = k

Here, k = number of sheetsweight of sheets in grams= 1240 =

Now x is the number of sheets of the paper which weigh 212 kg = g.

Using the relation x = ky, x =310 x 2500 =

Thus, 750 sheets of paper would weigh 212k.g

A train is moving at a uniform speed of 75 km/hour.

(i) How far will it travel in 20 minutes?

(ii) Find the time required to cover a distance of 250 km.

Solution:

Let the distance travelled (in km) in 20 minutes be x and time taken (in minutes) to cover 250 km be y.

Distance travelled (in km)	75	x	250
Time taken (in minutes)	60	20	y

Since the speed is uniform, therefore, the distance covered would be directly proportional to time.

(i) We have: 7560 = x20

x = 75×2060 =

So, the train will cover a distance of 25 km in 20 minutes.

(ii) Also, 7560 = 250y

y = 250×6075 = minutes or hours minutes

Therefore, 3 hours 20 minutes will be required to cover a distance of 250 kilometres.

Alternatively, when x is known, then one can determine y from the relation: x20 = 250y

You know that a map is a miniature representation of a very large region. A scale is usually given at the bottom of the map. The scale shows a relationship between actual length and the length represented on the map. The scale of the map is thus the ratio of the distance between two points on the map to the actual distance between two points on the large region.

For example: If 1 cm on the map represents 8 km of actual distance [i.e., the scale is 1 cm : 8 km or 1 : 800,000] then 2 cm on the same map will represent km.

Hence, we can say that scale of a map is based on the concept of direct proportion.

The scale of a map is given as 1:30000000. Two cities are 4 cm apart on the map. Find the actual distance between them.

Solution:

Instructions

Let the map distance be x cm and actual distance be y cm, then 1:30000000 = x : y

or 13x107 = xy

Since x = 4 so, 13x107 = 4y

or y = 4 × 3 × 107 = 12 × 107cm = km

Thus, two cities, which are 4 cm apart on the map, are actually 1200 km away from each other.

1. On a squared paper, draw five squares of different sides. Write the following information in a tabular form

	Square 1	Square 2	Square 3	Square 4	Square 5
Length of a side (L)
Perimeter (P)
LP
Area (A)
LA

Find whether the length of a side is in direct proportion to: (a) the perimeter of the square. (b) the area of the square.

2. The following ingredients are required to make halwa for 5 persons: Suji/Rawa = 250 g, Sugar = 300 g, Ghee = 200 g, Water = 500 mL. Using the concept of proportion, estimate the changes in the quantity of ingredients, to prepare halwa for your class.

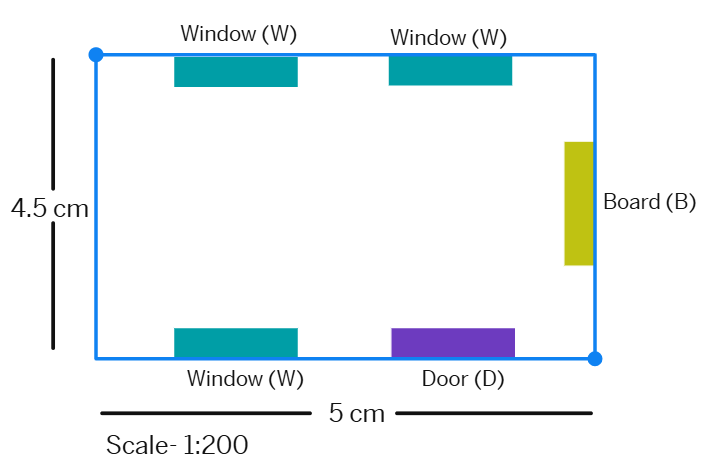
3. Choose a scale and make a map of your classroom, showing windows, doors, blackboard etc. (An example is given here).

Take a few problems discussed so far under ‘direct variation’. Do you think that they can be solved by ‘unitary method’?

Ratio Applications

Glossary

Direct Proportion

Sign in to Innings2

Ratio Applications

Reset Progress

Glossary

Direct Proportion