Exercise 3.3

Write the information given in the picture in the form of an equation. Also, find 'x' in the following figure.

Solution:

The total length of the spoon is cm.

The handle portion is given as cm,

and the remaining part (spoon head) is labeled as x cm.

Equation:

x+ 11 =

Solving for x:

x = 15 −

x = cm

So, the missing length x is 4 cm.

2 Write the information given in the picture in the form of an equation. Also, find 'y' in the following figure.

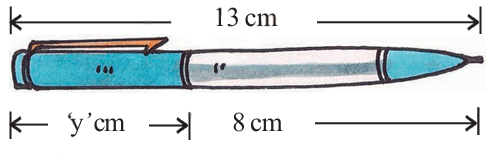
Solution:

The total length of the pen is cm.

The front portion of the pen is labeled as cm,

and the remaining part (back portion) is labeled as y cm.

Equation:

y + 8 =

Solving for y:

y = 13 − 8

y = cm

So, the missing length y is 5 cm.

3 If we add 7 to twice a number, we get 49. Find the number.

Solution:

Let's represent the unknown number as x.

According to the given condition:

2x + =

Solving for x:

Subtract 7 from both sides:

2x = 49 −

2x =

Divide both sides by 2:

x = 422

x =

The number is 21.

4 Find the number when multiplied by 7 and then reduced by 3 is equal to 53.

Solution:

Let's represent the unknown number as x.

According to the given condition:

7x − 3 =

Solving for x:

Add 3 to both sides:

7x = 53 +

7x =

Divide both sides by 7:

x = 567

x =

The number is 8.

5 Sum of two numbers is 95. If one exceeds the other by 3, find the numbers.

Solution:

Let's represent the two numbers as x and y.

Given conditions:

Their sum is 95:

x + y =

One number exceeds the other by 3:

x = y + 3

Solving for x and y:

Substitute x = y+3 into the sum equation:

(y+3) + y =

Simplify: 2y + 3 = 95

Subtract 3 from both sides:

2y =

Divide by 2:

y = 922 =

Find x:

x = y + 3 = 46 + 3 =

The two numbers are 46 and 49.

6 Sum of three consecutive integers is 24. Find the integers.

Solution:

Let's represent the three consecutive integers as x, x+1, and x+2.

Given condition:

x + (x+1) + (x+2) =

Solving for x:

Simplify the equation:

3x + 3 =

Subtract 3 from both sides:

3x =

Divide by 3:

x =

Finding the integers:

x = , x + 1 = , x + 2 =

The three consecutive integers are 7, 8, and 9.

7 . Find the length and breadth of the rectangle given below if it's perimeter is 72m

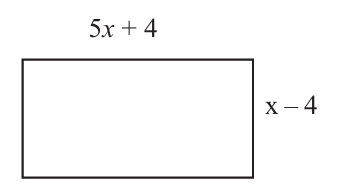
Solution:

Given:

Length of the rectangle = 5x + 4

Breadth of the rectangle = x − 4

Perimeter of the rectangle = meters

Perimeter = 2× (Length + Breadth)

Substituting the given values:

2 × [(5x + 4) + (x − 4)] = 72

Solving for xxx:

Simplify inside the brackets:

5x + 4 + x − 4 = x

So, the equation becomes:

2 × 6x =

Divide both sides by 2:

6x =

Divide by 6:

x = 366 =

Finding the Length and Breadth:

Length = 5(6) + 4 = 30 + 4 = meters

Breadth = 6 − 4 = 26 - 4 = 26 − 4 = meters

The length is 34 meters, and the breadth is 2 meters.

8. After 15 years, Hema's age will become four times that of her present age. Find her present age.

Solution:

Let's represent Hema's present age as x.

Given condition:

After 15 years, Hema's age will be four times her present age.

x + 15 =

Solving for x:

Subtract x from both sides:

15 = 4x − x

15 =

Divide both sides by 3:

x = 153 =

Hema's present age is 5 years.

9 A Sum of ₹ 3000 is to be given in the form of 63 prizes. If the prize money is either ₹ 100 or ₹ 25 . Find the number of prizes of each type.

Solution:

x as the number of ₹100 prizes.

y as the number of ₹25 prizes.

Given Conditions:

The total number of prizes is 63:

x + y =

The total prize money is ₹3000:

100x + 25y =

Solving for x and y:

Express y in terms of x

From the first equation: y = 63 − x

Substitute into the second equation

100x + 25 (63−x) =

100x + 15751475 − 25x = 3000

x + 1575 = 3000

Solve for x

75x = 3000 −

75x =

x = 142575 =

Find y

y = 63 − 19 =

The number of ₹100 prizes is 19.

The number of ₹25 prizes is 44.

10 A number is divided into two parts such that one part is 10 more than the other. If the two parts are in the ratio 5:3, find the number and the two parts.

Solution:

Let the two parts be 5x and 3x.

Since one part is 10 more than the other, we set up the equation:

= + 10

5x − 3x = 10

= 10

x = 102 =

Find the Two Parts

5x = 5(5) =

3x = 3(5) =

Find the Total Number

25 + 15 =

The number is 40.

The two parts are 25 and 15.

11 Suhana said, "multiplying my number by 5 and adding 8 it gives the same answer as subtracting my number from 20". Find Suhana's numbers.

Solution:

Let Suhana's number be x.

Multiplying the number by 5 and adding 8 gives the same result as subtracting the number from 20:

+ 8 = −

5x + x + 8 =

+ 8 = 20

6x =

Divide by 6:

x = 126 =

Suhana's number is 2.

12 The teacher tells the class that the highest marks obtained by a student in her class in twice the lowest marks plus 7. The highest mark is 87. What is the lowest mark?

Solution:

Let the lowest marks be x.

The highest marks are twice the lowest marks plus 7: Highest marks = + 7

Given that the highest marks are 87, we set up the equation:

87 = 2x + 7

87 − 7 = 2x

= 2x

x = 802 =

The lowest marks are 40.

13 In adjacent figure find the magnitude of each of the three angles formed ? (Hint: Sum of all angles at a point on a line is 180°)

Solution:

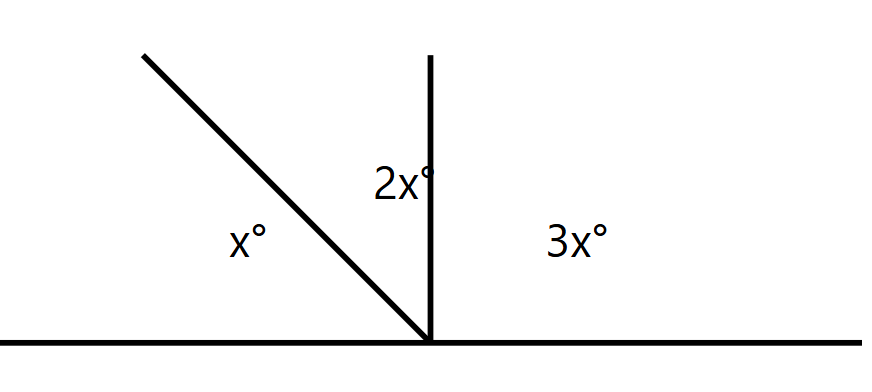
First angle = x°

Second angle = 2x°

Third angle = 3x°

The sum of all angles on a straight line is °.

x + 2x + 3x = 180

= 180

x= 1806 =

First angle = x = °

Second angle = 2x = 2(30) = °

Third angle = 3x = 3(30) = °

The three angles are 30°, 60°, and 90°.

14 Solve the following riddle:

Solution:

Let's define the unknown number as x.

Taking the number two times over means .

Adding thirty-six gives 2x + .

To reach 100 (a century), we still need 4.

So, the equation is:

2x + 36 + =

2x + = 100

2x =

x = 602 =

The number is 30.