Inverse Proportion
Two quantities may change in such a manner that if one quantity increases, the other quantity decreases and vice versa.
For example: As the number of workers increases, time taken to finish the job decreases. Similarly, if we increase the speed, the time taken to cover a given distance decreases. To understand this, let us look into the following situation.
Zaheeda can go to her school in four different ways. She can walk, run, cycle or go by car. Study the following table.
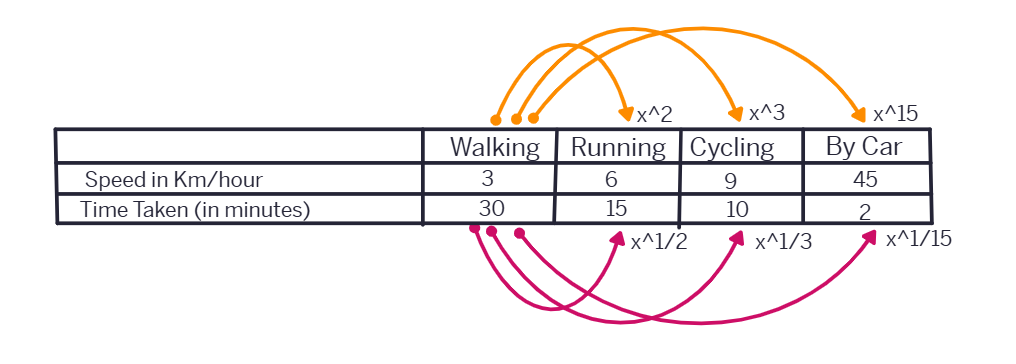
Observe that as the speed increases, time taken to cover the same distance decreases.
As Zaheeda doubles her speed by running, time reduces to half. As she increases her speed to three times by cycling, time decreases to one third. Similarly, as she increases her speed to 15 times, time decreases to one fifteenth. (Or, in other words the ratio by which time decreases is inverse of the ratio by which the corresponding speed increases).
Can we say that speed and time change inversely in proportion?
Multiplicative inverse of a number is its reciprocal. Thus,
Let us consider example. A school wants to spend ₹ 6000 on mathematics textbooks. How many books could be bought at ₹ 40 each?
Clearly 150 books can be bought. If the price of a textbook is more than ₹ 40, then the number of books which could be purchased with the same amount of money would be less than 150. Observe the following table.
| Price of each book (in ) | Number of books that can be bought |
|---|---|
| 40 | 150 |
| 50 | 120 |
| 60 | 100 |
| 75 | 80 |
| 80 | 75 |
| 100 | 60 |
If we represent the price of one book as x and the number of books bought as y, then as x increases y decreases and vice-versa. It is important to note that the product xy remains constant. We say that x varies inversely with y and y varies inversely with x. Thus two quantities x and y are said to vary in inverse proportion, if there exists a relation of the type xy = k between them, k being a constant.
If
We say that x and y are in
Hence, in this example, cost of a book and number of books purchased in a fixed amount are inversely proportional. Similarly, speed of a vehicle and the time taken to cover a fixed distance changes in inverse proportion.
Think of more such examples of pairs of quantities that vary in inverse proportion. You may now have a look at the furniture – arranging problem, stated in the introductory part of this chapter.
Here is an activity for better understanding of the inverse proportion below?
Observe the counters in 2 different ways.
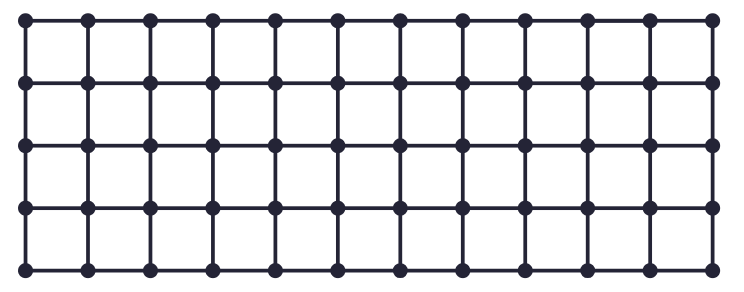

| Number of Rows (R) | Count | Number of Columns (C) | Count |
|---|---|---|---|
| (R1) | 2 | (C1) | 24 |
| (R2) | 3 | (C2) | 16 |
| (R3) | 4 | (C3) | 12 |
| (R4) | 6 | (C4) | 8 |
| (R5) | 8 | (C5) | 6 |
What do you observe? As R increases, C decreases.
For 2 rows there will be 24 columns. For 3 rows there are 16 columns, also for 8 rows there are 6 columns. By putting these values in table we get:
Observe the following tables and find which pair of variables (here x and y) are in inverse proportion.
(i)
| x | y |
|---|---|
| 50 | 5 |
| 40 | 6 |
| 30 | 7 |
| 20 | 8 |
| x | y | x × y |
|---|---|---|
| 50 | 5 | 50 × 5 = |
| 40 | 6 | 40 × 6 = |
| 30 | 7 | 30 × 7 = |
| 20 | 8 | 20 × 8 = |
Here, the product x×y is not constant (250, 240, 210, and 160), so x and y are
(ii)
| x | y |
|---|---|
| 100 | 60 |
| 200 | 30 |
| 300 | 20 |
| 400 | 15 |
| x | y | x × y |
|---|---|---|
| 100 | 60 | 100 × 60 = |
| 200 | 30 | 200 × 30 = |
| 300 | 20 | 300 × 20 = |
| 400 | 15 | 400 × 15 = |
In this table, the product x×y = 6000 is constant across all values, indicating that x and y are in inverse proportion in this table.
(iii)
| x | y |
|---|---|
| 90 | 10 |
| 60 | 15 |
| 45 | 20 |
| 30 | 25 |
| 20 | 30 |
| 5 | 35 |
| x | y | x × y |
|---|---|---|
| 90 | 10 | 90 × 10 = |
| 60 | 15 | 60 × 15 = |
| 45 | 20 | 45 × 20 = |
| 30 | 25 | 30 × 25 = |
| 20 | 30 | 20 × 30 = |
| 5 | 35 | 5 × 35 = |
The product x×y is not constant in this table (values are 900, 900, 900, 750, 600, and 175), so x and y are
When two quantities x and y are in direct proportion (or vary directly) they are also written as x∝ y.
When two quantities x and y are in inverse proportion (or vary inversely) they are also written as x ∝
6 pipes are required to fill a tank in 1 hour 20 minutes. How long will it take if only 5 pipes of the same type are used?
Solution:
Let the desired time to fill the tank be x minutes. Thus, we have the following table.
| Number of pipes | 6 | 5 |
|---|---|---|
| Time (in minutes) | 80 | x |
Lesser the number of pipes, more will be the time required by it to fill the tank. So, this is a case of inverse proportion. Hence, 80 × 6 = x × 5 [
x =
x =
Thus, time taken to fill the tank by 5 pipes is 96 minutes or 1 hour 36 minutes.
There are 100 students in a hostel. Food provision for them is for 20 days. How long will these provisions last, if 25 more students join the group?
Solution:
We have the following table.
| Number of students | Number of days |
|---|---|
| 100 | 20 |
| 125 | y |
Note that more the number of students, the sooner would the provisions exhaust. Therefore, this is a case of inverse proportion.
- So, 100 × 20 = 125 × y
- which gives the value of y
- y =
- Thus, the provisions will last for 16 days, if 25 more students join the hostel.
If 15 workers can build a wall in 48 hours, how many workers will be required to do the same work in 30 hours?
Solution
We have the following table.
| Number of hours | Number of workers |
|---|---|
| 48 | 15 |
| 30 | y |
1. Take a sheet of paper. Fold it as shown in the figure. Count the number of parts and the area of a part in each case.
(https://img.youtube.com/vi/VIDEO_ID_HERE/0.jpg)
Tabulate your observations and discuss with your friends.
Is it a case of inverse proportion? Why?
| Number of parts | Area of each part |
|---|---|
| 1 | area of the paper |
| 2 | |
| 4 | |
| 8 | |
| 16 |
