Quadrilaterals and their Properties
Now, let's look into the classifications of quadrilaterals based on the type of sides and angles it consists of. We can look at the
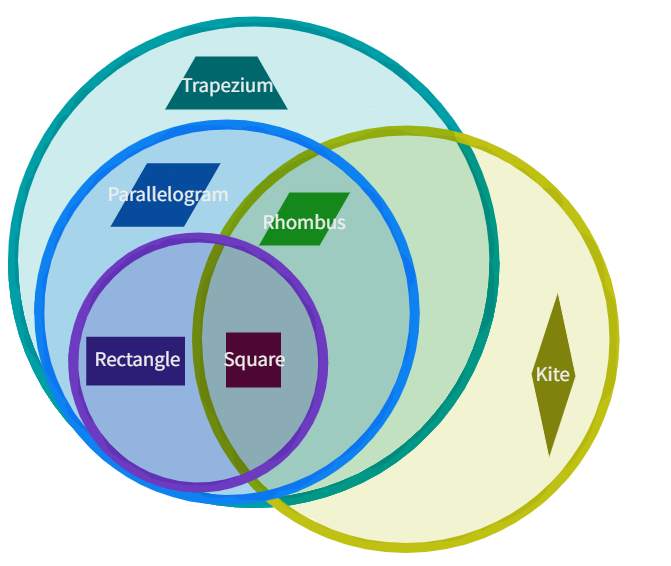
Venn Diagram for Quadrilaterals
(1) Trapezium
The
Usually, they consist of only one pair of opposite parallel sides. If the quadrilateral has two pairs of opposite parallel sides, the quadrilateral is further classified, as we will see further on.
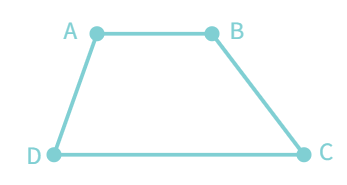
Scalene Trapezium
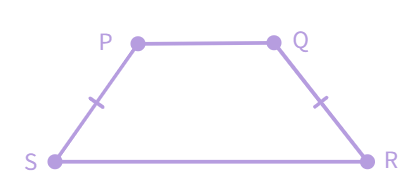
Isosceles Trapezium
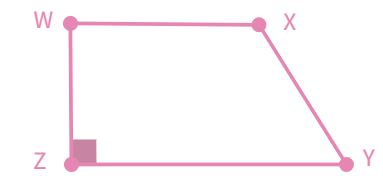
Right Trapezium
Trapeziums can further be divided into the following types:
Scalene Trapezium : The non-parallel lines are unequal in length.
Isosceles Trapezium : Non-parallel lines are equal in length.
Right Trapezium : Has atleast two adjacent right angles.
Let's try out an activity.
Using paper, make identical cut-outs of a triangle with sides 3 cm, 4 cm, 5 cm. If we take three cut-outs and try to form a quardrilateral with it, we will get a
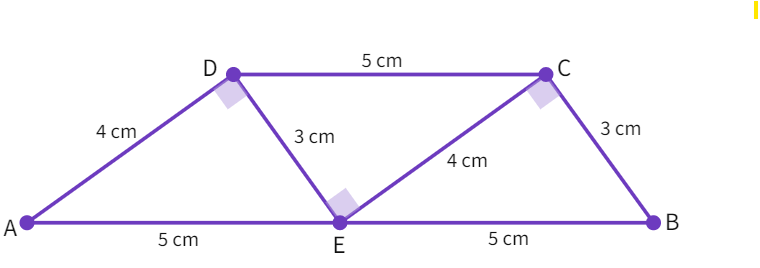
Arrangement
- Which are the parallel sides here?
- Are the non-parallel sides be equal?
- You have answered all the questions. Moving on.
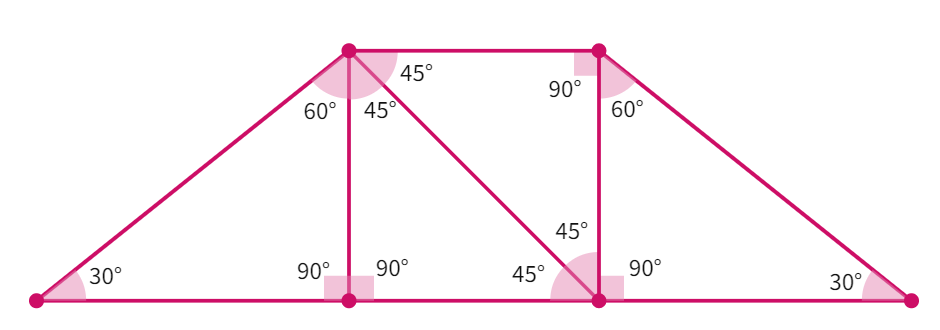
Activity: Take four set-squares from the geometry box. As in the earlier example try to form different types of trapeziums.
Can we obtain an isoceles trapezium while carrying out this activity?
Using all the four set squares, we can get an iscosceles trapezium by arranging as given below:
Kite
Kite is the type of a quadrilateral which has exactly two distinct consecutive pairs of sides of equal length.
Example of Kite Quadrilateral.
Note: The sides with the same markings in the above figure are equal. For example AB = AD and BC = CD.
(i) A kite has 4 sides (It is a quadrilateral).
(ii) There are exactly two distinct consecutive pairs of sides of equal length.
Think: Is a square also a kite?
Parallelogram
A parallelogram is a quadrilateral having opposite parallel sides.
Parallelogram.
Not a Parallelogram.
Now, is a rectangle also a parallelogram ?
Elements of a parallelogram
Now, let's discuss the properties of a parallelogram.
Parallelogram.
In the parallelogram ABCD figure given above:
- AB and DC and AD and BC are the
.
2. ∠A and ∠C and ∠B and ∠D form the pair of
3. AB and BC are
4. ∠A and ∠B and ∠B and ∠C are
Upon studying parallelograms, we find that:
Property: The opposite sides of a parallelogram are of equal length.
Opposite sides of a parallelogram
- Considering the triangles: ∆ABC and ∆ADC
- We see: ∠DAC = ∠
and ∠DCA = ∠ as they are angles - AC = AC as it is a
side - Therefore, ∆ ABC ≅ ∆ CDA by
congruency criterion. - Hence, AB =
and BC = - Therefore, we see that the opposite sides of a parallelogram are equal.
Try These
Take two identical set squares with angles 30° – 60° – 90° and place them adjacently to form a parallelogram as shown in Fig. Does this help you to verify the above property?
Property: The opposite sides of a parallelogram are of
As we can see in the figure above, the opposite sides of figure are equal.
The figure above is a
Example 3: Find the perimeter of the parallelogram PQRS.
Solution: In a parallelogram, the opposite sides have same length.
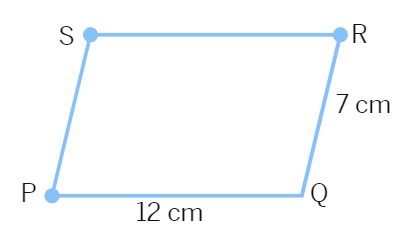
Therefore, PQ = SR =
So, Perimeter = PQ + QR + RS + SP = 12 cm + 7 cm + 12 cm + 7 cm =
Thus, the perimeter of the parallelogram PQRS is 38 cm.
Angles of a parallelogram
Moving on to the property concerning the (opposite) angles of a parallelogram.
Property: The opposite angles of a parallelogram are of equal measure.
Opposite angles of a parallelogram
- Considering the triangles- ∆ABC and ∆ADC , we know that ∆ ABC ≅ ∆ CDA by
congruency criterion. - Therefore, ∠ADC = ∠
. Similarly, if we join BD and consider the triangles- ∆ADB and ∆CBD, we get: ∠BAD = ∠ - Hence, opposite angles are equal for a parallelogram.
Try These
Take two identical 30° – 60° – 90° set squares and place them adjacently to form a parallelogram. Does the figure obtained help you to verify the above property?
Example 4: In the figure, BEST is a parallelogram. Find the values x, y and z.
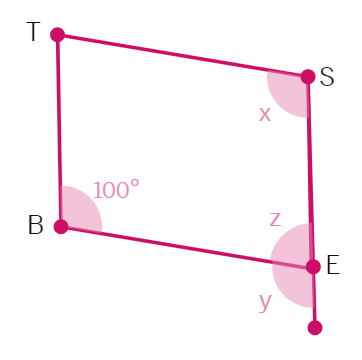
Solution: S is
So, x =
y =
z =
For the adjacent angles of a parallelogram:
Property: The adjacent angles in a parallelogram are supplementary.
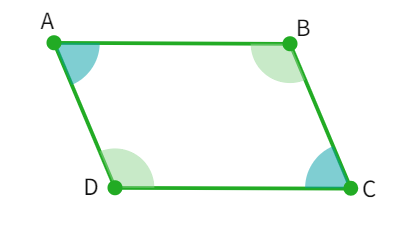
Adjacent angles of a parallelogram
- We know that, the co-interior angles in a pair of parallel lines are
to each other. - As AB||DC with AD being the transverse cutting it, we can say: ∠A + ∠D =
° - Similarly, the side BC also acts like a
for the parallel sides AB and DC, giving ∠B + ∠C = ° - Now, as AD||BC are a pair of parallel lines with AB and DC as the transverse, we get: ∠A + ∠B = ∠D + ∠C =
° - Therefore, the sum of any two adjacent angles of a parallelogram is equal to 180°
Example 5: In a parallelogram RING, if m∠R = 70°, find all the other angles.
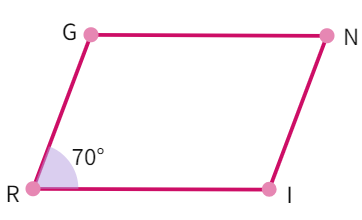
Parallelogram RING
- From the figure, we know that: ∠N =
° - As the opposite angles of a parallelogram are equal. We also know that, Sum of any two adjacent angles of a parallelogram is equal to 180°.
- Therefore, ∠N + ∠I =
° - ∠I =
° - °. Thus, ∠I = ° - Thus, m∠I =
° m∠N = ° m∠G = °
After showing m∠R = m∠N = 70°, can you find m∠I and m∠G by any other method?
Alternate Solution: Using the formula for sum of interior angles of a polygon:
Sum of interior angles of a polygon = (n - 2) x 180°
where n is the number of sides
Putting n =
Sum of interior angles =
We know that, ∠I = ∠G from the parallelogram properties.
Therefore we have,
∠R + ∠I + ∠N + ∠G = 360°
70° + 2∠I + 70° = 360°
∠I =
Therefore,
∠I = ∠G = 110°
Diagonals of a parallelogram
Generally speaking, the diagonals of a parallelogram are not of equal length. However, the diagonals of a parallelogram share an interesting property.
Property: The diagonals of a parallelogram bisect each other with respect to the point of intersection.
Diagonals of a parallelogram
- Considering the triangles- ∆PQT and ∆SRT, we see that: PQ =
as they are sides of a parallelogram - We also have: ∠TPQ = ∠
and ∠TQP = ∠ as they are angles - Thus, by
congruency criterion- ∆ PQT ≅ ∆ - This means PT =
and RT = - Therefore, the diagonals of a parallelogram
each other.
Example 6: In the figure, HELP is a parallelogram. (Lengths are in cms). Given that OE = 4 and HL is 5 more than PE? Find OH.
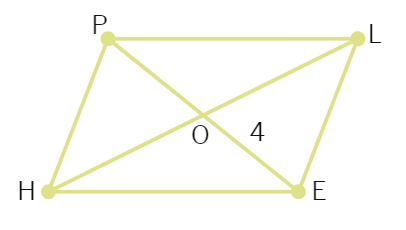
Solution: If OE = 4 then OP also is
So, PE =
Therefore, HL = 8 +
Hence OH =
Thus, OH = 6.5 (cms)
Rhombus
A rhombus is a quadrilateral with sides of equal length. Since the opposite sides of a rhombus have the same length, it is also a type of parallelogram.
An interesting property of a rhombus is that it is a special case of a kite and parallelogram. This is despite the fact that the properties of a kite and a parallelogram have nothing in common. Therefore, a rhombus consists of properties of a parallelogram and a kite as well.
As for the diagonals of a rhombus:
Property: The diagonals of a rhombus are perpendicular bisectors of one another.
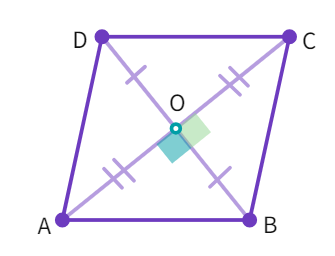
Diagonals of a Rhombus
- A rhombus is also a
where we know, the diagonals each other. - Therefore, considering the triangles- ∆AOB and ∆COB, we get OA =
- We also have AB =
as they are of a rhombus and OB is a side. - Thus, by
congruency criterion- ∆ AOB ≅ ∆ - We also see that ∠AOB and ∠COB are equal and have an angle sum of
° - Thus, m ∠AOB = m ∠COB =
° - Therefore, the diagonals of a rhombus perpendicularly
each other.
Example 7: RICE is a rhombus. Find x, y, z. Justify your findings.
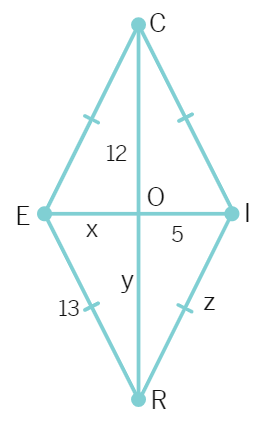
Solution:
x = OE = OI (diagonals
y = OR = OC =
z = side of the rhombus =
Thus, x = 5 , y = 12 and z = 13
Rectangle
A rectangle is a type of parallelogram in which every angle equal. Therefore, it has all the properties of a parallelogram:
(1) Opposite sides of equal length and
(2) Diagonals bisect each other.
Since all the angles are equal in a rectangle and the total sum of the interior angles for a quadrilateral is 360°, we get that:
Each angle = 90°
Note: In a parallelogram, the diagonals can be of different lengths but in a rectangle, the diagonals are of equal lengths.
Property: The diagonals of a rectangle are of equal length.
Diagonals of a Rectangle
- Considering the triangles ∆ ABC and ∆BAD: AB =
as it is a side. - We also have: BC = AD as they are
sides and m ∠A = m ∠B = ° as all angles are angles. - Therefore, by
criterion: ∆ ABC ≅ ∆ - Which gives us, AC =
- Therefore, in a rectangle the diagonals are equal in length and also bisect each other.
From the above conclusion, we can say that: In a rectangle the diagonals, besides being equal in length
Example 8: RENT is a rectangle. Its diagonals meet at O. Find x, if OR = 2x + 4 and OT = 3x + 1
Solution:
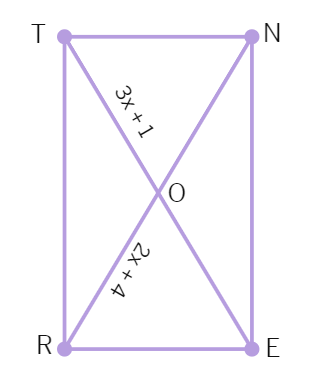
OT is half of the diagonal TE and OR is half of the diagonal RN (as diagonals
Diagonals are
So, their halves are also equal.
Therefore, 3x + 1 = 2x + 4 ⇒ x =
Square
A square is further, a special case of a
Therefore, like earlier, a square has properties of a rectangle while having all sides equal.
In a square, the diagonals have the following properties:
(i) bisect one another (Square is a type of parallelogram)
(ii) are of equal length (Square is a type of rectangle) and
(iii) bisect each other perpendicularly.
So, now we need to prove the following property:
Property: The diagonals of a square are perpendicular bisectors of each other.
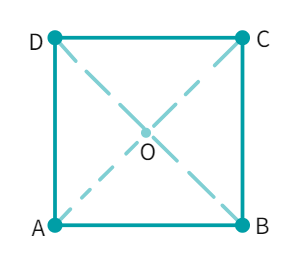
Diagonals of a square
- With O as the point of intersection for the diagonals, consider the triangles- ∆AOD and ∆COD
- We have: AD =
as all sides are equal, OD is a side and OA = as diagonals each other. - Therefore, by
congruency criterion: ∆AOD ≅ ∆ - Thus we get, m∠AOD = m∠
- Since the angles are a linear pair we get, m∠AOD = m∠COD =
° - Therefore, the diagonals of a square are
bisectors of each other.
Let's Solve
A mason has made a concrete slab. He needs it to be rectangular. Answer Yes/No for the following below mentioned properties that need to be vertified in order to make sure that it is rectangular?
Explanation:
We need to check for all the properties of a rectangle which include:
(1) Diagonals are equal in length.
(2) All angles have a measure of 90°.
(3) Opposite sides are parallel and equal
Answer the following:
| Quadrilateral | Properties | Image |
|---|---|---|
| 1. Parallelogram | (1) Opposite sides are (2) Opposite angles are (3) Diagonals | 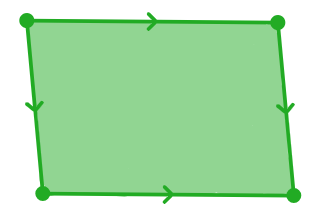 |
| 2. Rhombus | (1) All the properties of a (2) Diagonals are | 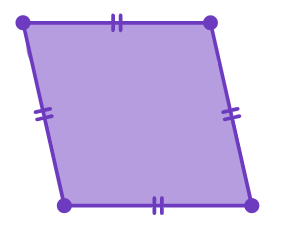 |
| 3. Rectangle | (1) All the properties of a (2) Each of the angles is a (3) Diagonals are |  |
| 4. Square | All the properties of a parallelogram, rhombus and | 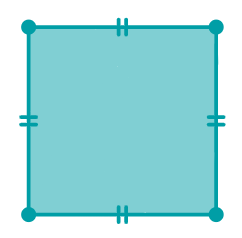 |
| 5. Kite | (1) The diagonals are (2) One of the diagonals bisects the other (3) In the figure, the angles made by the adjacent unequal sides are equal. | 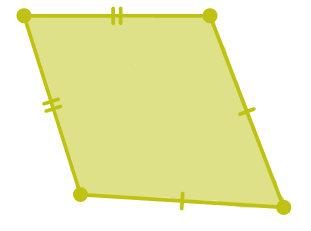 |
