Innings2
Create New Account

Sign in to Innings2

or

New Account     Reset Password     

Chapter 14: Surface Areas and Volume (Cube and Cuboid)

    Introduction

    Cuboid

    Cube

    Volume of Cube and Cuboid

    Exercise 14.1

    Exercise 14.2

    What We Have Discussed?

    Easy Level Worksheet

    Moderate Level Worksheet

    Hard Level Worksheet

Powered by Innings 2

Reset Progress

This will delete your progress and chat data for all chapters in this course, and cannot be undone!

Glossary

Select one of the keywords on the left…

Chapter 14: Surface Areas and Volume (Cube and Cuboid) > Cube

Cube

In the case of cuboid, the length, breadth and height is assumed to be of unequal numerical values. But if

length(l) = breadth(b) = height (h) for a cuboid

We get a cube. Just like a cuboid, a cube also has a total number of 6 faces but each face is a square, instead of a rectangle. We already know that the area of a square with side length 'a' is:

Thus,

Total surface area of cube =

The total surface area of a cube = 6a2 where, a is the length of a side.

Find the surface area of cube A and lateral surface area of cube B.

Instructions

For cube A with side length 10 cm: Total surface area = × side2 = 6 × = 6 × = cm2
For cube B: the lateral surface area is 8 cm. We know that lateral surface area of a cube = × side2
So 4 × side2 = 8 cm which gives us: side2 = ÷ = cm. Thus, side = cm
Total surface area = 6 × side2 = 6 × = cm2

How will you arrange 12 cubes of equal length to form a cuboid of smallest surface area?

Instructions

Think about all the possible arrangements

  • The possible arrangements include:
  • 12×1×1, 2×3×2 and 6×2×1
  • Calculating the surface area for each:
  • For: 12×1×1 = cm2, 2×3×2 = cm2, 6×2×1 = cm2
  • Thus, we have found the arrangement with the smallest surface area i.e.

Two cubes each with side b are joined to form a cuboid.

Instructions

Finding surface area of two cubes together

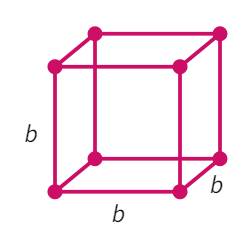
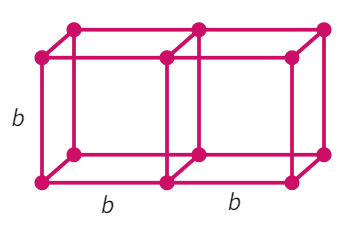
  • When two cubes are together: l = , b = and h =
  • Thus, surface area of this cuboid:
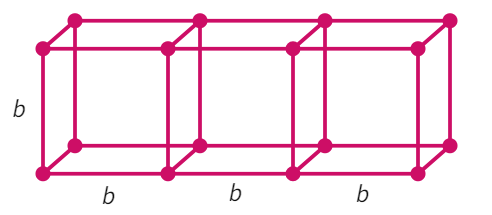
  • When three cubes are put together: l = , b = and h =
  • Thus, surface area of the second cuboid:
  • We have found the desired answers.

Lateral surface area (cuboid) = Base Perimeter × h

In general,

The formulae of Lateral Surface Area for cube, cuboid and cylinder is base perimeter multiplied into height.

Find the surface area and the lateral surface area of a cube of side equal to 5 units.

Instructions

Putting the value in the respective equations

  • We know that, total surface area of cube: unit2
  • And the lateral surface area of cube: unit2
  • Substituting the value we get
  • Total surface area of cube: unit2
  • Lateral surface area of cube: unit2
  • We got the respective results.

If the cube in the previous question is elongated to a height of 10 units, it becomes a and the new surface area and the lateral surface area are:

Instructions

The new length is 10 units

  • We know that, total surface area of cuboid of length(l), breadth(b) and height(h): unit2
  • And the lateral surface area of cuboid: unit2
  • Substituting the values we get
  • Total surface area of cuboid: unit2
  • Lateral surface area of cuboid: unit2
  • We have found the respective results.