Cuboid

Say, we have a cuboidal, cubical and a cylindrical box- all having the same height. If these boxes need to be painted, can you deduce which box requires more amount of paint? Logically, we know that the box with the most amount of surface area will be using up more paint? But which box has the highest value of surface area?

To find the total surface area of any object, we need to find the area of each face of that object and add up all the values. Thus,

The surface area of a solid is the sum of the areas of its faces.

Cuboid

A cuboid is a 3D object, having the length, breadth and height as dimensions (the values for atleast two dimensions is unequal) and the opposite faces are identical.

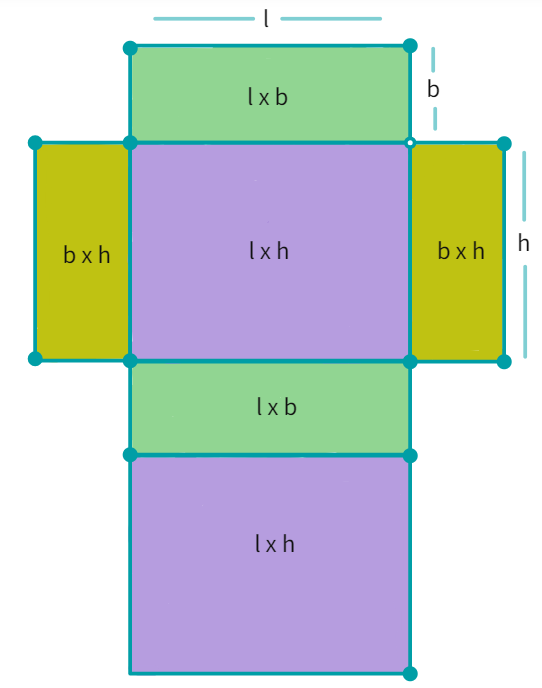
Since, a cuboid has a total of six faces- it has pairs of identical faces.

To find the total surface area:

The Total surface area of a cuboid = h × l + b × l + b × h + l × h + b × h + l × b

= 2(lb + bh + hl)

When we consider, the surface of a room to be painted, how much paint will be needed? We realize that the roof and floor need not be included for this calculation. Like this, there are many cases where only the sides (excluding the top and base) of the solid need to be taken into account. In such cases, we calculate the lateral surface area.

In the case regarding the room, we calculate the lateral surface area of the cuboid.

Can we say that:

Total surface area of cuboid = lateral surface area + 2 × area of base? (Yes/No)

We have a cuboid with length (l), breadth(b) and height (h), where the numerical values for all the dimensions are different.If we interchange the length and the height of the cuboid to obtain a new cuboid, will its lateral surface area change? (Yes/No)

The new lateral surface area will be equal to:

Given: length = 15 cm , breadth = 10 cm and height = 20cm, find the value of the surface area of the cuboid.

Instructions

TRY THESE

Find the total surface area of the following cuboids:

Instructions