Enhanced Curriculum Support
This is a comprehensive educational resource designed to provide students with the tools and guidance necessary to excel. This support system is structured to cater to various aspects of learning, ensuring that students are well-prepared for academic challenges and practical applications of mathematical concepts. Some are the key benefits are mentioned below:
1.Comprehensive Learning: This holistic approach helps students gain a thorough understanding of the subject. Practical Application: The resources encourage students to apply mathematical concepts to real-life scenarios, enhancing their practical understanding and problem-solving skills.
2.Critical Thinking and Reasoning: Value-Based and HOTS questions promote critical thinking and reasoning abilities. These skills are crucial for students to tackle complex problems and make informed decisions.
3.Exam Preparedness: Sample Question Papers and Practice Questions provide ample practice for exams. They help students familiarize themselves with the exam format and types of questions, reducing exam anxiety.
4.Ethical and Moral Development: Value-Based Questions integrate ethical and moral lessons into the learning process, helping in the overall development of students' character and social responsibility. By incorporating these diverse elements, Enhanced Curriculum Support aims to provide a robust and well-rounded knowledge, preparing students for both academic success and real-world challenges.
Sample Questions
SecA
1. In the adjoining figure, if AB ∥ DE, then the measure of ACD is :
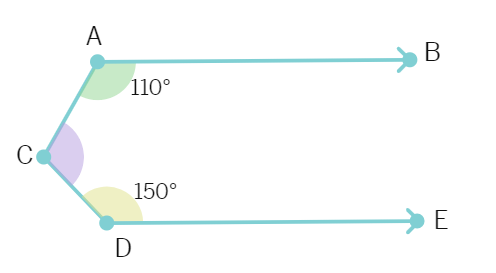
(a) 90° (b) 100° (c) 80° (d) 70°
2. In the given figure, straight lines AB and CD intersect at O. If ∠AOC = ϕ, ∠BOC = θ and θ = 3ϕ, then ϕ = ?
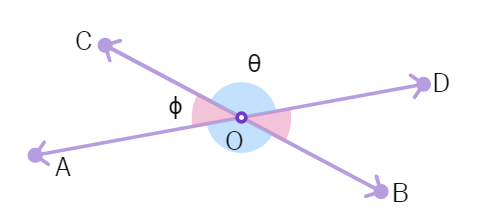
(a) 40° (b) 30° (c) 45° (d) 60°
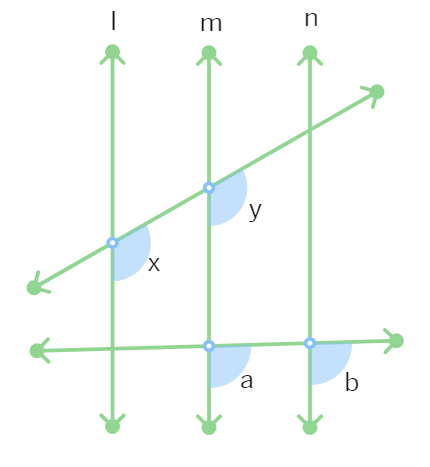
3. Given that lines l1, l2 and l3 in figure are parallel. The value of x is:
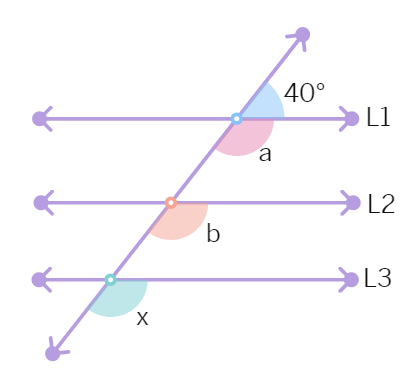
(a) 140° (b) 40° (c) 50° (d) 80°
4. In the given figure, straight lines AB and CD intersect at O. If ∠AOC + ∠BOD = 130°, then ∠AOD = ?
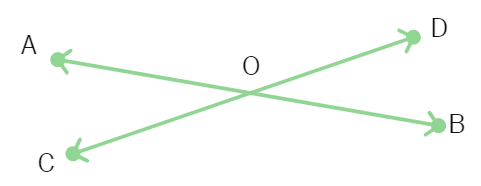
(a) 110° (b) 65° (c) 115° (d) 125°
5. In the given figure x = 30°, the value of Y is:
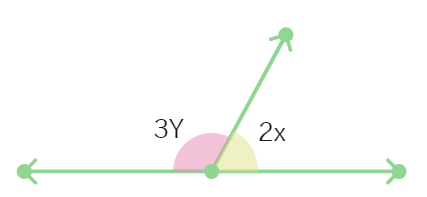
(a) 45° (b) 40° (c) 10° (d) 36°
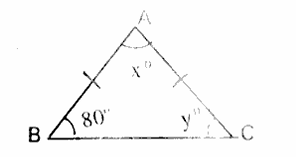
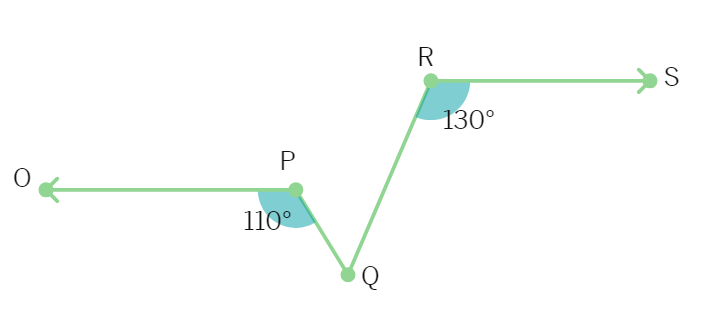
6. Using information given in the adjacent figure find the value of 'x' and 'y'.
7. The angles of a triangle are in the ratio 1 : 2 : 3. Find the angles.
SecB
1. Read the following two statements which are taken as axioms:
(i) If two lines intersect each other, then the vertically opposite angles are not equal.
(ii) If a ray stands on a line, then the sum of two adjacent angles so formed is equal to 180°.
Is this system of axioms consistent? Justify your answer.
2. Two angles form a linear pair. If one angle is 70°, find the other angle and explain why their sum is 180°.
3. Two lines intersect at a point. If one of the angles formed is 65°, find the measures of the other three angles and justify your answer using the property of vertically opposite angles.
4. If two parallel lines are cut by a transversal, and one of the corresponding angles is 50°, find the measures of all the remaining angles formed at the points of intersection.
5. Two parallel lines are cut by a transversal. If one of the alternate interior angles is 85°, find all the angles formed and explain your reasoning.
6. In a triangle, the exterior angle is 120°, and one of the interior opposite angles is 50°. Find the other interior opposite angle.
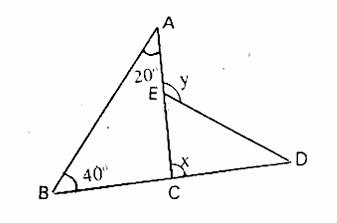
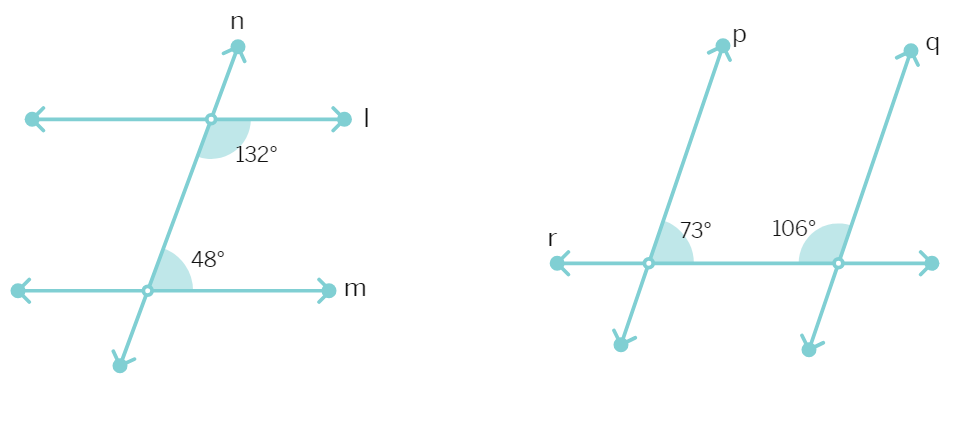
7. Using information given in the adjacent figure, find the value of x + y.
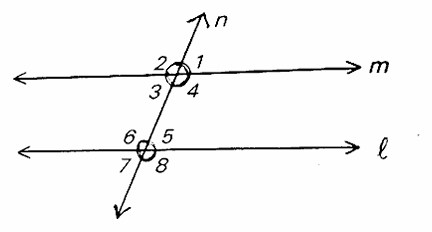
8. In the adjacent figure ℓ ∥ m, n is a transversal, ∠4 = 80°. Find the angles which are equal to ∠4. Give reasons.
9. If an angle is double of its complement, find the angles.
SecC
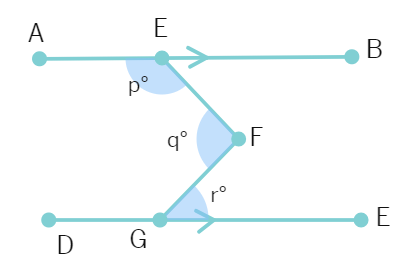
1. In the given figure, AB || CD. Prove that p + q - r = 180°.
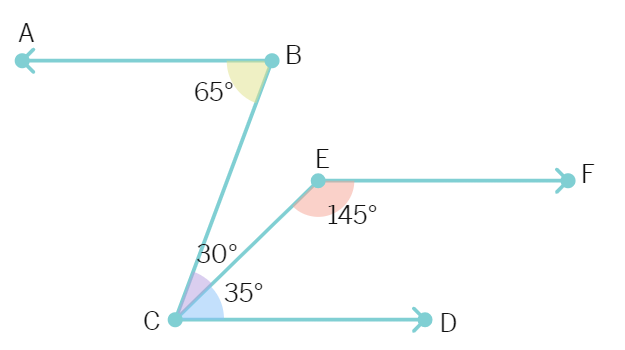
2. In figure, ∠ ABC = 65°, BCE = 30°, DCE = 35° and CFE = 145°. Prove that AB || EF.
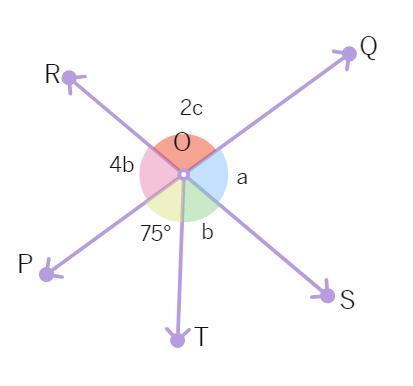
3. In the fig, two straight lines PQ and RS intersect each other at O, if POT = 75° Find the values of a, b and c.
4. Two lines are cut by a transversal. If a pair of alternate interior angles is 3x+10° and 5x−20°, find the value of x and determine the measures of all angles formed at the points of intersection.
5.If two parallel lines are cut by a transversal such that one pair of alternate interior angles is equal to 75°, prove that the lines are parallel, and determine the measures of all the angles formed by the transversal.
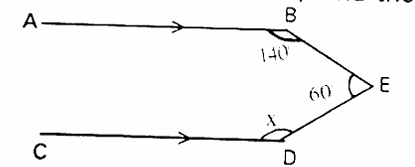
6. From the figure find, 'x' and 'y'.
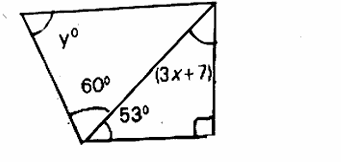
7. In the adjacent figure, AB ∥ CD, Find the value of 'x'.
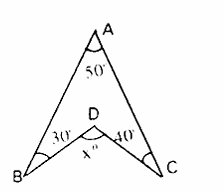
8. Using the information given in the adjacent figure, find the value of 'x'.
Sec D
1. In a triangle, the exterior angle is equal to the sum of the two interior opposite angles. Using this property, find the angles of a triangle whose exterior angle is 130°, and verify the angle sum property of the triangle.
2. In a pair of parallel lines intersected by a transversal, one of the alternate interior angles is 45°. Find all the angles formed and prove that they satisfy the properties of parallel lines.
3. A ladder leans against a wall making an angle of 60° with the ground. The top of the ladder is 4 meters above the ground. Find the length of the ladder and the angle of elevation from the base of the ladder to the top. Explain the reasoning using trigonometric principles and geometry.
Value Based Questions
Problem 1
City planners are designing a new road system that involves creating intersections at specific angles to optimize traffic flow and safety. One planner proposes slightly altering the angle of a critical intersection to accommodate a new commercial development, even though it might lead to increased traffic congestion in the future.
The planners originally designed an intersection with angles of 70° and 110°. If the planner suggests altering one angle to 75°, calculate the new angle formed at the intersection and discuss how this change could impact traffic flow and safety.
Analyze the ethical implications of altering the planned angle of the intersection for short-term gains. How do the principles of lines and angles relate to long-term planning and community welfare? What should the city planners prioritize to ensure a balance between development and public safety?
Problem 2
An artist is creating a geometric mural on a public building, using various angles and lines to form intricate patterns. The artist’s assistant, tasked with drawing the initial guidelines, suggests using approximate angles to save time. However, the artist insists on using exact angles to ensure the design’s symmetry and visual appeal.
In one part of the mural, the artist needs to draw a triangle with angles 30°, 60°, and 90 °. The assistant mistakenly draws one angle as 32 °. Calculate the error and discuss how this small change could affect the symmetry and overall appearance of the mural.
Discuss how precision in using lines and angles contributes to the overall quality of artistic and design projects. What values are reflected in the artist’s insistence on accuracy? How does this attention to detail influence the viewer’s perception of the artwork and the artist’s reputation?
Problem 3
During a geometry class, students are asked to work in groups to solve problems related to lines and angles. One of the problems requires the students to prove that vertically opposite angles are equal when two lines intersect. Some group members have different approaches to solving the problem, leading to a disagreement.
In the problem, the group finds that one of the vertically opposite angles is 72°. Calculate the measure of the other vertically opposite angle and justify the solution using the properties of intersecting lines.
Reflect on the importance of collaboration and respect for different viewpoints when working in a group. How can the group members resolve their differences and find a solution that everyone agrees on? Why is it important to listen to and consider each member’s approach, especially in academic and professional settings?
HOTS
Q1
Consider a trapezium ABCD with AB parallel to CD. If ∠BCD =
Q2
Given two parallel lines and a transversal, if the difference between an exterior angle and the corresponding interior angle is 40°, find the measure of each of the angles formed by the transversal.
In quadrilateral ABCD, it is given that
Q3
In a triangle ABC, D and E are points on sides AB and AC, respectively, such that DE is parallel to BC. Prove that
Practice Questions
Select the correct option
Questions
1. If two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 2 : 3, then the greater of the two angles is:
(A) 54° (B) 108°
(C) 120° (D) 136°
2. The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is:
(A) an acute angled triangle (B) an obtuse angled triangle
(C) a right triangle (D) an isosceles triangle
3. If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be:
(A) 50° (B) 65°
(C) 145° (D) 155°
4. In the figure, if AB || CD || EF, PQ || RS, ∠RQD = 25° and ∠CQP = 60°, then ∠QRS is equal to:
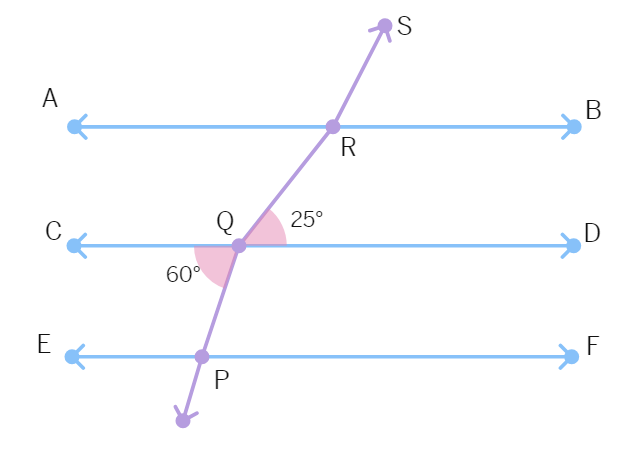
(A) 85° (B) 135°
(C) 145° (D) 110°
5. If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be:
(A) 50° (B) 65°
(C) 145° (D) 155°
6. Angles of a triangle are in the ratio 2 : 4 : 3. The smallest angle of the triangle is:
(A) 60° (B) 40°
(C) 80° (D) 20°
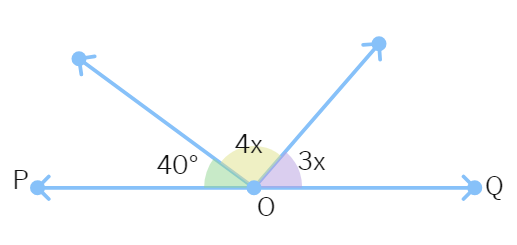
7. In the figure, POQ is a line. The value of x is:
(A) 20° (B) 25°
(C) 30° (D) 35°
8. In the figure, if OP||RS, ∠OPQ = 110° and ∠QRS = 130°, then ∠ PQR is equal to:
(A) 40° (B) 50°
(C) 60° (D) 70°
9. The conjugate angle of 80° is: (A) 100° (B) 10° (C) 280° (D) 190°
10. Manvi says, "90° is the conjugate angle of 270°." Do you agree with her? Justify your answer.
11. Diagram which represents vertically opposite angles.
img(src="/content/scert/9/lines_angles/images/fig_10.png" width=250 height=100)Answer the given below questions
Questions
9. In the figure, which of the two lines are parallel and why?
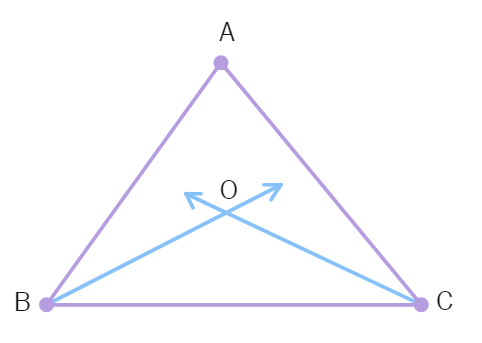
10. Let OA, OB, OC and OD are rays in the anticlockwise direction such that ∠ AOB = ∠COD = 100°, ∠BOC = 82° and ∠AOD = 78°. Is it true to say that AOC and BOD are lines?
11. Can a triangle have two obtuse angles? Give reason for your answer.
12. A transversal intersects two lines in such a way that the two interior angles on the same side of the transversal are equal. Will the two lines always be parallel? Give reason for your answer.
13. How many triangles can be drawn having its angles as 45°, 64° and 72°? Give reason for your answer.
14. How many triangles can be drawn having its angles as 53°, 64° and 63°? Give reason for your answer.
15. Two adjacent angles are equal. Is it necessary that each of these angles will be a right angle? Justify your answer.
16. If one of the angles formed by two intersecting lines is a right angle, what can you say about the other three angles? Give reason for your answer.
17. A triangle ABC is right angled at A. L is a point on BC such that AL ⊥ BC. Prove that ∠ BAL = ∠ ACB.
18. Two lines are respectively perpendicular to two parallel lines. Show that they are parallel to each other.
19. Bisectors of interior ∠B and exterior ∠ACD of a ∆ ABC intersect at the point T. Prove that ∠ BTC =
20. Prove that through a given point, we can draw only one perpendicular to a given line. [Hint: Use proof by contradiction].
21. Prove that two lines that are respectively perpendicular to two intersecting lines intersect each other.[Hint: Use proof by contradiction].
22. Prove that a triangle must have atleast two acute angles.
23. In the below figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM =
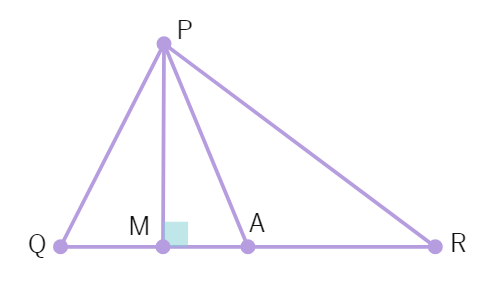
24. Bisectors of angles B and C of a triangle ABC intersect each other at the point O. Prove that ∠BOC = 90° +
25. In the figure, m and n are two plane mirrors perpendicular to each other. Show that incident ray CA is parallel to reflected ray BD.
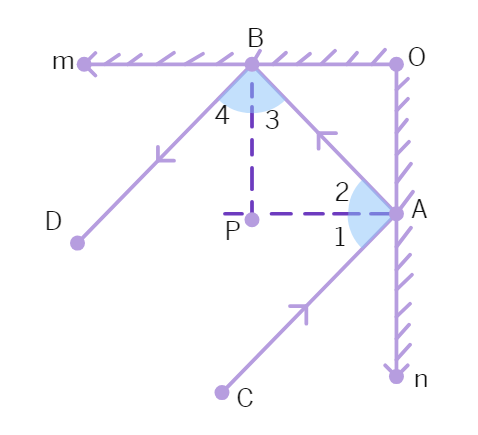
26. In the figure, DE || QR and AP and BP are bisectors of ∠ EAB and ∠ RBA, respectively. Find ∠APB.
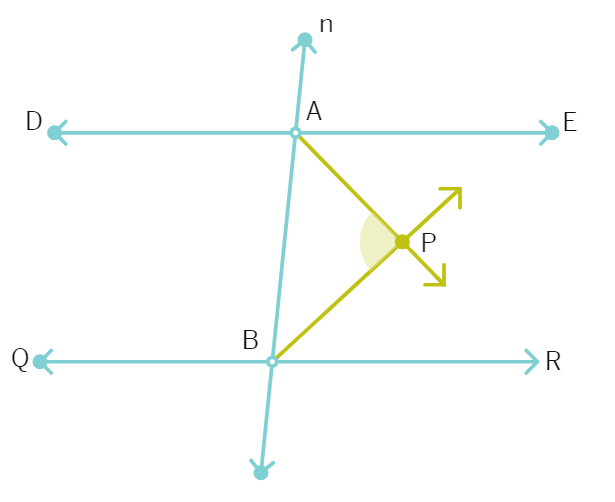
27. In the figure, OD is the bisector of ∠AOC, OE is the bisector of ∠BOC and OD ⊥ OE. Show that the points A, O and B are collinear.
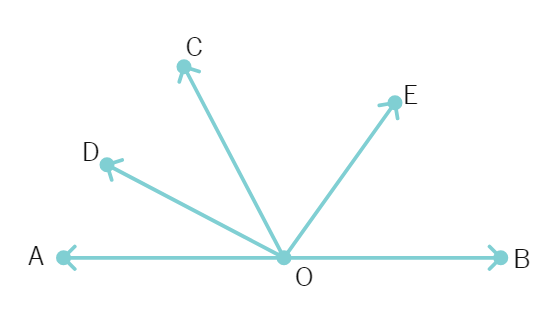
28. In the figure, AB, CD and EF are three lines concurrent at O. Find the value of y.
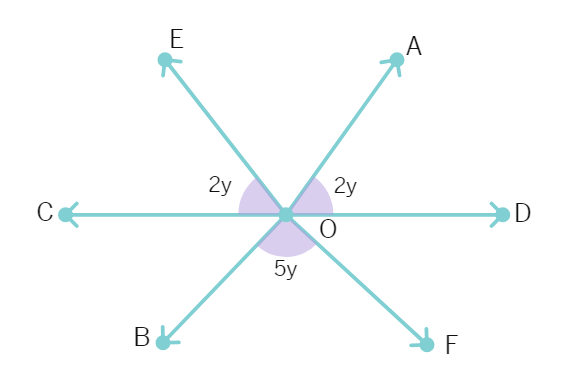
29. In the figure, x = y and a = b. Prove that l || n.
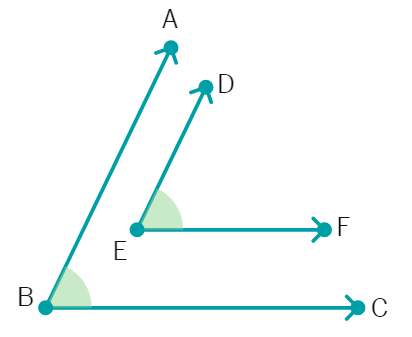
30. In the figure, BA || ED and BC || EF. Show that ∠ABC = ∠DEF [Hint: Produce DE to intersect BC at P (say)].
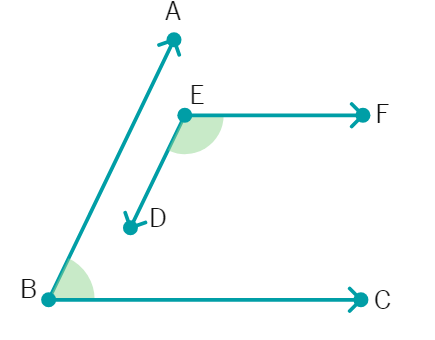
31. In the figure, BA || ED and BC || EF. Show that ∠ ABC + ∠ DEF = 180°.
Case Based Questions
Q1
A bridge crosses a river in such a way that the roads leading to the bridge form corresponding angles with the bridge. The angle between the road and the bridge on the left side is 70°, and on the right side, it is x°. The bridge and roads are straight, and the roads are parallel to each other.
1. Find the value of x.
2. If a vehicle travels along the road on the left side, turns at the bridge, and then travels along the road on the right side, what angle does it turn through at the bridge?
3. Assume a second parallel road is constructed 10 meters away from the first road, and a pedestrian pathway is built perpendicular to the roads connecting them. What angle does this pathway make with the bridge? Based on the given angles, explain why the bridge and roads cannot form a right triangle.
Sol 1
1.
Since the roads are parallel and the bridge acts as a transversal, the angles formed are corresponding angles.
According to Euclid’s axiom:
Therefore, x = 70°.
2.
The vehicle turns through the exterior angle formed between the two roads at the bridge.
- The exterior angle is given by: 180° - 70° = 110°
Thus, the vehicle turns through an angle of 110° at the bridge.
3.
The pedestrian pathway is perpendicular to the roads, meaning it makes a 90° angle with each road.
Since the roads are parallel and the bridge is a transversal, the angle between the pedestrian pathway and the bridge can be found as the complement of the angle between the bridge and the road: 90° - 70° = 20°
Thus, the pedestrian pathway makes an angle of 20° with the bridge.
Why the bridge and roads cannot form a right triangle:
For a right triangle to exist:
- One of the angles must be 90°.
- The given angles between the roads and the bridge 70° and 70° are equal, indicating symmetry, and neither forms a right angle.
The bridge and roads cannot form a right triangle because:
- The corresponding angles 70° are not 90°.
- Both roads are parallel, and the transversal bridge cannot create a 90° angle with one and a different angle with the other.
Hence, no right triangle can be formed.
Q2
A ladder is leaning against a wall such that it makes an angle of 60° with the ground. The top of the ladder reaches a point 4 meters above the ground. A person standing on the ground sees the top of the ladder and the point where the ladder touches the ground, forming a straight line. The angle of elevation from the person to the top of the ladder is θ.
1. Find the value of θ if the person is standing at a point 2 meters away from the base of the ladder.
2. Calculate the length of the ladder.
3. If the person moves 1 meter closer to the ladder, how will the angle of elevation change? Explain your reasoning.
4. Is the ladder perpendicular to the wall? If not, what angle does it make with the wall?
Sol 2
1. To find the angle of elevation θ, we use the tangent function:
tanθ =
Sunstituting the values: tanθ =
Using the inverse tangent function: θ =
The angle of elevation θ is approximately 63.43°.
2. Using the sine function, which relates the angle, the height, and the hypotenuse (the length of the ladder):
sin(60°) =
Substitute the values: sin(60°) =
Since sin(60°) =
length of the ladder =
The length of the ladder is approximately 4.62meters.
3.
If the person moves 1 meter closer, their distance from the base of the ladder becomes 2 − 1 = 1meter. The new angle of elevation
4
The ladder is not perpendicular to the wall. The angle between the ladder and the wall can be calculated as the complement of the angle it makes with the ground:
Angle with the wall = 90°Angle with the ground
Substituting the value:
Angle with the wall = 90° - 60° = 30°
The ladder makes an angle of 30° with the wall.
