Lines and a Transversal
Activity: Take a piece of paper and randomly, draw any number of pairs of lines.There will always be two types of lines that we would encounter:
(1) Intersecting Lines
(2) Parallel Lines
Above we can see that lines PR and QS are
For parallel lines, the lengths of the common perpendiculars at different points along the line are the same and this length is called the distance between two parallel lines.
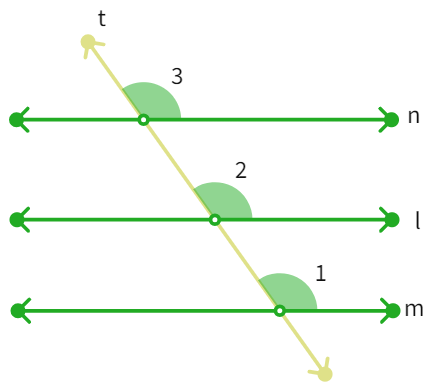
If two lines are parallel to the same line, are the two lines parallel to each other? In the above figure:
line m || line l and
line n || line l.
If we draw a transversal line t for the parallel lines, we already know that:
∠ 1 = ∠
So, ∠ 1 = ∠
Since, ∠ 1 and ∠ 3 are the corresponding angles for the parallel lines m and n, we can therefore, say that:
Line m || Line n (Converse of corresponding angles axiom)
Thus, we can state this in the form of the following theorem:
Theorem : Lines which are parallel to the same line are parallel to each other.
Given the same reasoning, this property can be extended to more than
Activity: Take a ruled paper and draw a pair of parallel lines coinciding with the ink lines. Draw a random transverse line which cuts both the lines. Measure the corresponding angles.
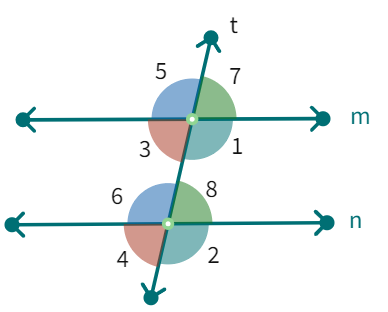
This activity illustrates the following fact:
If two parallel lines are cut by a transversal, each pair of corresponding angles are equal in measure.
We can use this result to get another interesting result. Look at figure above.
When 't' cuts the parallel lines, m and n, we get : ∠3 = ∠7 (vertically opposite angles).
But also, ∠7 = ∠8 (corresponding angles).
Therefore, ∠3 = ∠
Similarly we can show that ∠1 = ∠
Thus, we have the following result:
If two parallel lines are cut by a transversal, each pair of alternate interior angles are equal
∠3 + ∠1 =
But ∠1 = ∠6 (A pair of
Therefore, we can say that ∠3 + ∠6 =
Similarly, ∠1 + ∠8 =
Thus, we obtain the following result:
If two parallel lines are cut by a transversal, then each pair of interior angles on the same side of the transversal are supplementary.
Example 4: In the figure, if PQ || RS, ∠ MXQ = 135° and ∠ MYR = 40°, ∠ XMY will be equal to:
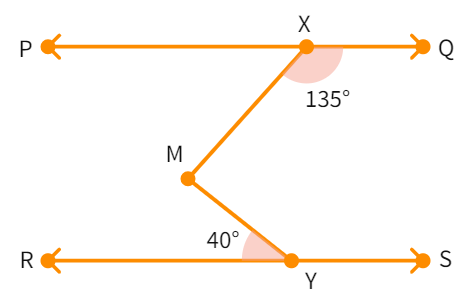
First construct a line AB parallel to line PQ and passing through point M.

Now, AB ||
AB ||
- Now, ∠ QXM + ∠ XMB =
° and ∠ QXM = 135° - Thus, ∠ XMB = 45° (1)
- We also know ∠ BMY = ∠ MYR as they are
angles - Thus, ∠ BMY =
° (2) - Upon adding (1) and (2) we get : ∠ XMY = ∠
+ ∠ - So, ∠ XMY =
° + ° = ° - We have found the answer
Example 5: If a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel.
Let's take the following: PQ and RS are two lines with a transversal AD as shown. The corresponding angles ∠ ABQ and ∠ BCS have angle bisectors BE and CG, respectively which are parallel to each other.
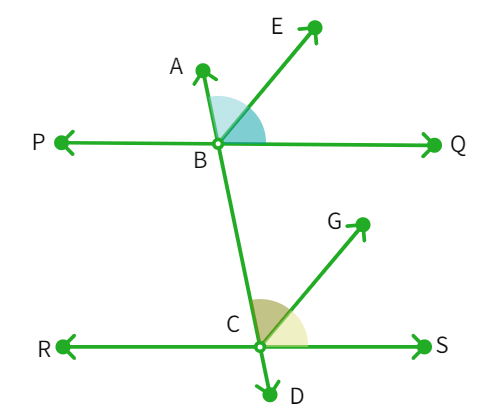
- Since, ray BE and CG are bisectors of ∠ ABQ and ∠ BCS.
- Thus, ∠ ABE =
∠ ABQ and ∠ BCG = ∠ BCS - We can also see that BE || CG and AD is the
. - ∠ ABE = ∠ BCG are
angles - Putting (1) and (2) in (3) we get
- As the
angles formed by transversal AD with PQ and RS are : PQ || RS
Example 6: In the figure, AB || CD, CD || EF and EA ⊥ AB. If ∠ BEF = 55°, find the values of x, y and z.
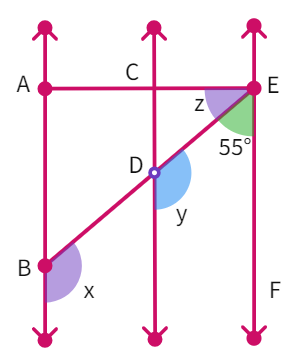
- We see that y + 55° = 180° as they are
angles on the same side of the transversal. - Thus, y =
° - We also have y =
as they are angles - Which gives us x =
° - We have been given that ∠ EAB =
° - So, ∠ EAB + ∠
= 180° which gives z = ° - We found all the answers.
