Reasoning in Mathematics
Let's start with a new card puzzle to understand deductive reasoning:
Imagine you have four cards with shapes on one side and colors on the other:
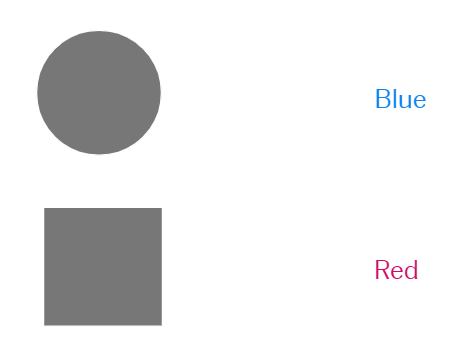
The rule is: "If a card has a curved shape on one side, then it must have a warm color on the other side."
verify this rule, which cards do you need to flip? Let's think through it:
Circle card: Must check because it's curved - need to verify it has a warm color.
Square card: Don't need to check because the rule doesn't make claims about non-curved shapes.
Blue card: Must check because if it has a curved shape on the other side, it violates the rule (blue is cool)
Red card: Don't need to check because even if it has a curved shape, it doesn't violate the rule (red is warm)
So you only need to flip the Circle and Blue cards - just like in the original puzzle, you need minimum checks to verify the rule.
Now let's contrast deductive vs inductive reasoning
Deductive Reasoning (Mathematics):
Starts with established rules/premises
Follows logical steps to reach a guaranteed conclusion
Example: "All squares have four equal sides. This shape has four equal sides. Therefore, this shape is a square." (Note: This particular example is actually flawed - can you spot why?)
Inductive Reasoning (Science):
Starts with observations
Forms patterns and hypotheses
Tests and refines based on evidence
Example: "Every swan I've seen is white. Therefore, I hypothesize all swans are white." (This can be disproven by finding a black swan)
A cybersecurity analyst uses both types of reasoning:
Deductive: "If there's unauthorized access AND it came from this IP AND it used these credentials, then it must be a breach from inside our network."
Inductive: "We've seen several failed login attempts followed by successful logins. This pattern suggests someone might be using a brute force attack."
The key difference is that deductive reasoning, when done correctly, leads to certainty, while inductive reasoning leads to probability and requires continuous testing and refinement.
