Exercise 1.2
1. Classify the following numbers as rational or irrational.
(i) 27
Solution:
The number is rational number:
=
Since
Therefore,
(ii)
Solution:
The number is rational number:
Therefore
(iii) 30.232342345…
Solution:
The number is rational number:
Since the decimal part is
(iv) 7.484848…
Solution:
The number is rational number:
Since the decimal part is
(v) 11.2132435465
Solution:
The number is rational number:
Since the decimal part is
(vi) 0.3030030003.....
Solution:
The number is rational number:
Since the decimal part is
2. Give four examples for rational and irrational numbers?
Solution:
Rational Numbers:
Irrational Numbers:
3. Find an irrational number between
Solution:
Convert the fractions to decimals (approximately):
There are
One irrational number between them:
4. Find two irrational numbers between 0.7 and 0.77
Solution:
Any random
Two irrational numbers between them:
5. Find the value of
Solution:
- Starting from right place a bar on top of every pair of digits. If a single digit remains on the left, add a bar to that as well. For eg: 5.
- From the left, find the square which is less than or equal to the digit. Here we have, (
2 2 3 2 when subtracting 2 2 - Bring down the number under the next bar (i.e. 00) to the right of the remainder. We now get the new dividend i.e.
- In the divisor, put the first digit as double the quotient and place a blank its right. i.e. 4_
- Put the largest possible digit to fill the blank which will also become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the product is less than or equal to the dividend.
- As
× 2 = 84, we can choose the digit to be filled in the blank as . - Now, the remainder is
and we bring down another pair of zeroes giving us: and the new divisor becomes twice of 22 i.e. 44_. - As
× 3 = 1329, we fill the blank with the number . - This process can be continued further. So, the
5 (upto two decimal places)
6. Find the value of
Solution:
- Starting from right place a bar on top of every pair of digits. If a single digit remains on the left, add a bar to that as well. For eg: 70000.
- From the left, find the square which is less than or equal to the digit. Here we have, (
2 2 3 2 when subtracting 2 2 - Bring down the number under the next bar (i.e. 00) to the right of the remainder. We now get the new dividend i.e.
- In the divisor put the first digit as double the quotient and place a blank its right. i.e. 4_
- Put the largest possible digit to fill the blank which will also become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the product is less than or equal to the dividend.
- As
× 6 = 276, we can choose the digit to be filled in the blank as . - Since, the remainder is
and we bring down another pair of zeroes giving us: and the new divisor becomes twice of 26 i.e. 52_. - As
× 4 = 2096, we fill the blank with the number . - This process can be continued further. So, the
7 (upto two decimal places)
7. Locate
Solution:
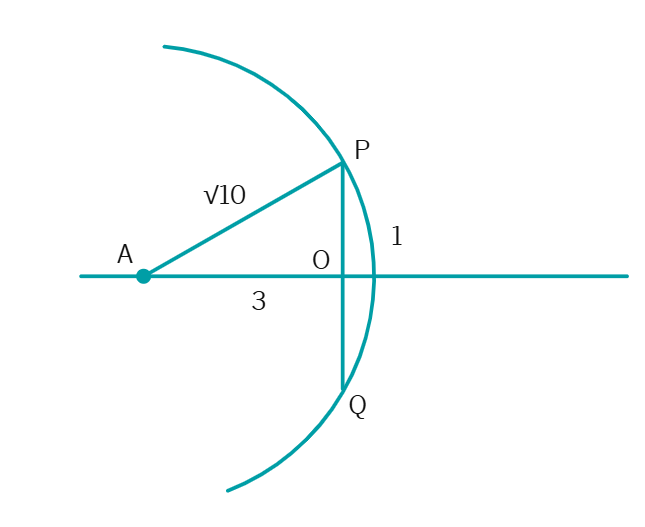
We can do it by using Pythagoras Theorem. We have:
Construction:
Take a line segment AO =
Draw a perpendicular on O and draw a line OP =
Now join AP with
Take A as center and
The line segment
8. Find at least two irrational numbers between 2 and 3.
Solution:
so the numbers between 4 and 9 are not perfect squares hence the square root of those numbers are irrational and they lay between 2 and 3.
Which are
9State whether the following statements are true or false. Justify your answers.
(i) Every irrational number is a real number.
Solution:
Real numbers include both rational and irrational numbers.
9. (ii) Every rational number is a real number.
Solution:
Real numbers include both rational and irrational numbers.
9. (iii) Every real number need not be a rational number
Solution:
Real numbers can be irrational.
9. (iv)
Solution:
The square root of a perfect square is a whole number (rational).
9. (v)
Solution:
The square root of a non-perfect square is irrational.
9. (vi) All real numbers are irrational
Solution:
Real numbers include both rational and irrational numbers.
