Criteria for Similarity of Triangles

In the previous section, we stated that two triangles are similar, if (i) their corresponding angles are equal and (ii) their corresponding sides are in the same ratio (or proportion).

That is, in △ ABC and △ DEF, if

(i) ∠A = ∠D, ∠B = ∠E, ∠C = ∠F and

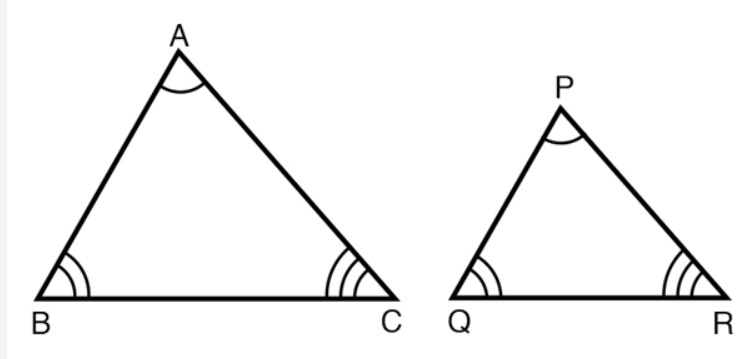
(ii)ABDE = BCEF = CAFD, then the two triangles are similar.(From the below fig)

Here, you can see that A corresponds to D, B corresponds to E and C corresponds to F. Symbolically, we write the similarity of these two triangles as '△ABC ~ △DEF' and read it as ‘triangle ABC is similar to triangle DEF’. The symbol ‘~’ stands for ‘is similar to’. Recall that you have used the symbol ‘≅’ for ‘is congruent to’ in Class IX.

It must be noted that as done in the case of congruency of two triangles, the similarity of two triangles should also be expressed symbolically, using correct correspondence of their vertices. For example, for the triangles ABC and DEF of above Fig, we cannot write '△ABC ~ △EDF' or '△ABC ~ △FED'. However, we can write '△BAC ~ △EDF'

Activity 4 :

Draw two line segments BC say 3 cm respectively. Then, at the points B and C respectively, construct angles PBC and QCB of some measures, say, 60° and 40°.

Instructions

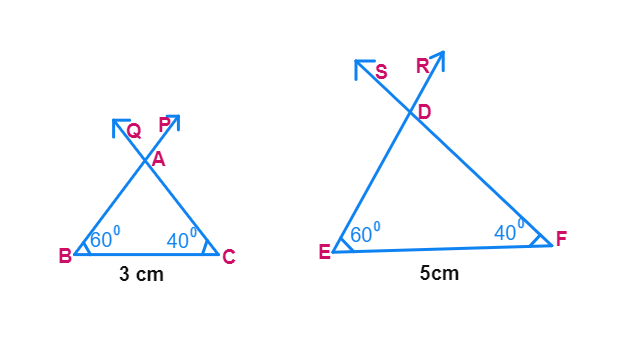
When corresponding angles of two triangles are equal, their corresponding sides are proportional. This means that if you have two triangles ABC and DEF where ∠B = ∠E, ∠C = ∠F, and ∠A = ∠D, then their corresponding sides are in the same ratio. For example, if BCEF = , then ABDE and CAFD are also approximately equal to . This leads us to a criterion for similarity: if two triangles have corresponding angles equal, then they are similar, and their corresponding sides are in proportion.

If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar.

This criterion is referred to as the AAA (Angle–Angle–Angle) criterion of similarity of two triangles. This theorem can be proved by taking two triangles ABC and DEF such that ∠ A = ∠ D, ∠ B = ∠ E and ∠ C = ∠ F (see in fig)

Cut DP = AB and DQ = AC and join PQ.

So, △ABC ≅ △

This gives ∠B = ∠ = ∠ and PQ ||

Therefore, DPPE = DQQF

Therefore, ABDE =

Similarly, ABDE = BCEF and so ABDE = BCEF = ACDF

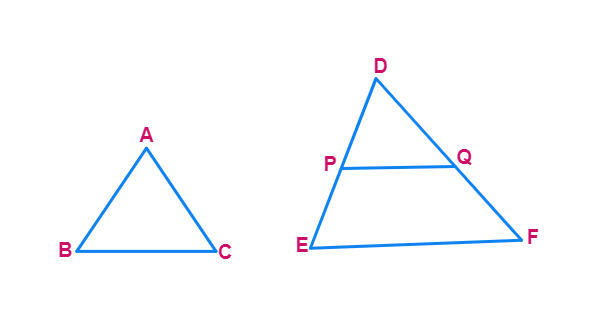
Remark : If two angles of a triangle are respectively equal to two angles of another triangle, then by the angle sum property of a triangle their third angles will also be equal.

If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are .

This may be referred to as the AA similarity criterion for two triangles.

Draw two triangles ABC and DEF such that AB = 3 cm, BC = 6 cm, CA = 8 cm, DE = 4.5 cm, EF = 9 cm and FD = 12 cm (see Fig).

Instructions

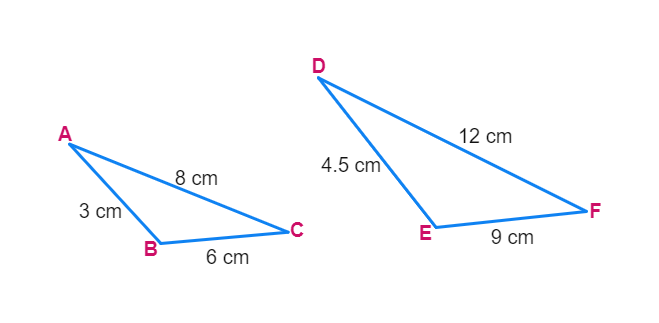
So, you have :

ABDE = BCEF = CAFD (each equal to 23)

Now measure ∠A= ∠D, ∠B = ∠E and ∠C =∠F, i.e., the corresponding angles of the two triangles are .

If in two triangles, sides of one triangle are proportional to (i.e., in the same ratio of ) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similiar.

This criterion is referred to as the SSS (Side–Side–Side) similarity criterion for two triangles.

Prove two triangles are similar

This theorem can be proved by taking two triangles ABC and DEF such that ABDE = BCEF = CAFD < 1
Cut DP = AB and DQ = and join PQ.
It can be seen that DPPE = DQQF and PQ ||
So, ∠P = ∠ and ∠Q = ∠.
Therefore, DP/ = DQ/ = PQ/
So, DPDE = DQDF = BC/
So, BC =
Thus, △ABC ~== △
So, ∠A = ∠, ∠B = ∠ and ∠C = ∠

Remark : You may recall that either of the two conditions namely, (i) corresponding angles are equal and (ii) corresponding sides are in the same ratio is not sufficient for two polygons to be similar. However, on the basis of Theorems 6.3 and 6.4, you can now say that in case of similarity of the two triangles, it is not necessary to check both the conditions as one condition implies the other.

If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.

This criterion is referred to as the SAS (Side–Angle–Side) similarity criterion for two triangles.

As before, this theorem can be proved by taking two triangles ABC and DEF such that ABDE = ACDF (< 1) and ∠A = ∠D

Cut DP = AB, DQ = and join PQ. (shown in fig).

Now, PQ || EF and △ ABC ~== △

So, ∠A = ∠D, ∠B = ∠P and ∠C = ∠Q

Therefore, △ ABC ~ △DEF

In shown in below Fig, if PQ || RS, prove that △ POQ~ △ SOR.

Prove that

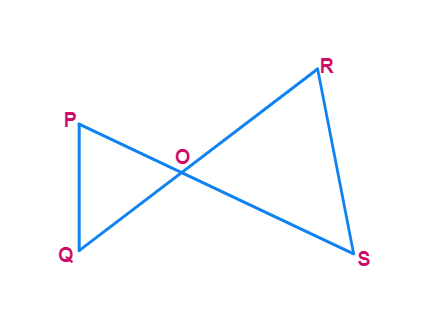
It is given that
So, Alternate angles ∠P = ∠
and ∠Q = ∠
Also, ∠POQ = ∠ (Vertically opposite angles)
Therefore, △POQ ~ △ (AAA similarity criterion)

Observe Fig. 6.30 and then find ∠P

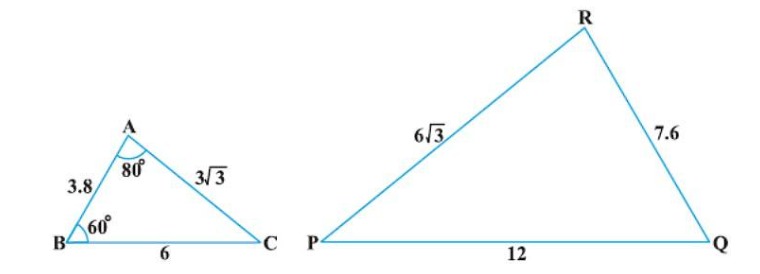
Solution:

In △ ABC and △ PQR,

ABRQ = 3.87.6 =

BCQP = 612 =

and CAPR= 3sqrt3/6sqrt3 =

That is, ABRQ = BCQP =

So,△ ABC ~ △ (SSS similarity)

Therefore,∠ C = ∠ (Corresponding angles of triangles)

But ∠ C = ° – ∠ A – ∠ (Angle sum property)

= 180° – 80° – 60° = °

So, ∠ P = °

In Fig, OA . OB = OC . OD. Show that ∠ A = ∠ C and ∠ B = ∠ D.

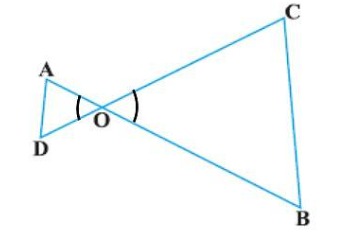
Solution:

OA . OB = OC . OD (Given)

So, OAOC = -------->(1)

Also, we have ∠ AOD = ∠ (Vertically opposite )----> (2)

Therefore, from (1) and (2), ∠ AOD ∠ COB (SAS similarity criterion)

So, ∠ A = ∠ and ∠ D = ∠ (Corresponding angles of triangles)

A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2 m/s. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.

find the length of girl shadow

Let AB denote the lamp-post and CD the girl after walking for 4 seconds away from the lamp-post. Let DE be metres.
Now, BD = 1.2 m × 4 = m.
Note that in △ABE and △CDE,

Sign in to Innings2

Triangles

Reset Progress

Glossary

Criteria for Similarity of Triangles