Similarity of Triangles
The concept of similarity is particularly powerful with triangles. We already know that the corresponding internal angles in similar polygons are
For triangles, the opposite is also true: this means that if you have two triangles with the same three angle sizes, then the triangles must be
Two triangles are similiar, if
(i) their corresponding angles are equal and
(ii) their corresponding sides are in the same ratio (or proportion).
The two triangles are said to be
The ratio of any two corresponding sides in two equiangular triangles is always the same. It is believed that he had used a result called the Basic Proportionality Theorem (now known as the Thales Theorem) for the same.
Let us perform the following activity to understand the Basic Proportionality Theorem:
Any angle XAY and on its one arm AX, mark points (say five points) P, Q, D, R and B such that AP = PQ = QD = DR = RB.
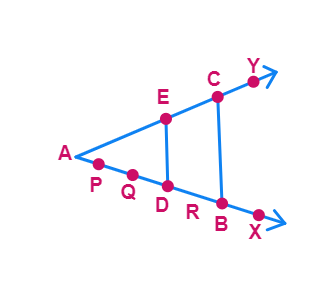
Do you observe from your constructions that
Measure AE and EC. Observe that
Thus, you can see that in △ABC, DE || BC and
Is it a coincidence?
it is due to the following theorem (known as the Basic Proportionality Theorem.)
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Proof :
We are given a triangle ABC in which a line parallel to side BC intersects other two sides AB and AC at D and E respectively(seen in figure).
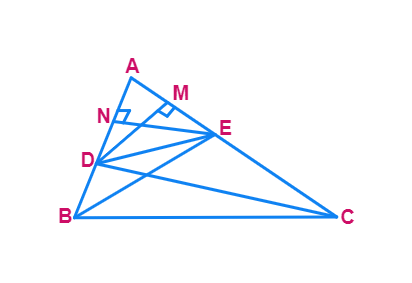
- Let us join BE and CD and then draw DM ⊥ AC and EN ⊥ AB.Now, area of △ADE (
1 2 1 2 × - area of △ADE is denoted as ar(ADE).So, ar(ADE) =
1 2 - Similarly, ar(BDE) =
1 2 × - And ar(ADE) =
1 2 × - And ar(DEC) =
1 2 × - Therefore,
ar ADE ar BDE - Hence we get the answer is
- and
ar ADE ar DCE - Hence we get the answer is
- Note that △BDE and DEC are on the same base DE and between the same parallels BC and DE. So, ar(BDE) = ar(DEC)
- Therefore, from (1), (2) and (3), we have :
- Is the converse of this theorem also true
Draw an angle XAY on your notebook and on ray AX, mark points
Similarly, on ray AY, mark points
If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
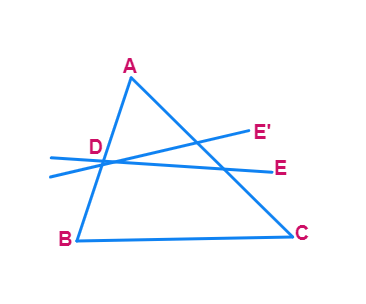
This theorem can be proved by taking a line DE such that
If DE is not parallel to BC, draw a line DE' parallel to
So,
Therefore
Adding 1 to both sides of above, you can see that E and E' must
If two angles in one triangle are congruent to two angles in another triangle, the two triangles are similar.
1. If a line intersects sides AB and AC of a △ ABC at D and E respectively and is parallel to BC, prove that
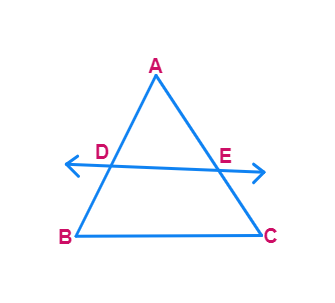
- Given DE ||
- From (Theorem 6.1)
AD DB - Or,
DB AD EC AE - add the value 1 for both sides
DB AD = EC AE - Or,
- So the sides are
=
2. ABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Show that
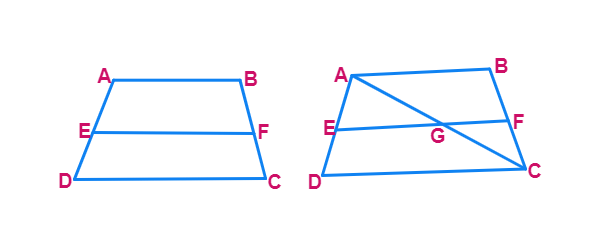
- Let us join AC to intersect EF at G(shown in fig). AB ||
and EF || - So, EF ||
(Lines parallel to the same line are parallel to each other) - Now, in △ADC, EG ||
(As EF || DC) - So,
AE ED / (Theorem 6.1) - Similarly, from △ CAB, =
- Therefore
AG GC / - Therefore, from (1) and (2),
AE ED /
3. In Fig shown
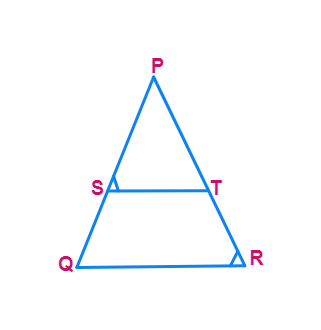
- It is given that
- From (Theorem 6.2) ST ||
- Therefore, ∠PST = ∠
(Corresponding angles) - Also, it is given that
- So, ∠PRQ= ∠
[From (1) and (2)] - Therefore, PQ =
(Sides opposite the equal angles) - i.e., PQR is an isosceles triangle.
