Innings2
Create New Account

Sign in to Innings2

or

New Account     Reset Password     

Chapter 10: Mensuration

    Introduction

    Perimeter

    Area

    Exercise 10.1

    Exercise 10.2

    Exercise 10.3

    What Have We Discussed ?

    Enhanced Curriculum Support

Powered by Innings 2

Reset Progress

This will delete your progress and chat data for all chapters in this course, and cannot be undone!

Glossary

Select one of the keywords on the left…

Chapter 10: Mensuration > Exercise 10.3

Exercise 10.3

1. Find the areas of the rectangles whose sides.

(a) 3 cm and 4 cm

Instructions

Length of the rectangle = cm
Breadth of the rectangle = cm
Area of the rectangle = l × b = 3 × 4 = sq cm.

(b) 12 m and 21 m

Length of the rectangle = m
Breadth of the rectangle = m
Area of the rectangle = l × b = 12 × 21 = sq m.

(c) 2 km and 3 km

Length of the rectangle = km
Breadth of the rectangle = km
Area of the rectangle = l × b = 2 × 3 = sq km.

(d) 2 m and 70 cm

Length of the rectangle = m
Breadth of the rectangle = cm
Area of the rectangle = l × b = 2 × = sq m.

2. Find the areas of the squares whose sides are.

(a) 10 cm

Area of the square = side × side = × = sq cm.

(b) 14 cm

Area of the square = side × side = × = sq cm.

(c) 5 m

Area of the square = side × side = × = sq cm.

The length and breadth of three rectangles are as given below.

Which one has the largest area and which one has the smallest?

(a) 9 m and 6 m

Instructions

Length of the rectangle = cm
Breadth of the rectangle = cm
Area of the rectangle = l × b = 9 × 6 = sq cm.

(b) 17 m and 3 m

Length of the rectangle = cm
Breadth of the rectangle = cm
Area of the rectangle = l × b = 17 × 3 = sq cm.

(c) 4 m and 14 m

Length of the rectangle = cm
Breadth of the rectangle = cm
Area of the rectangle = l × b = 4 × 14 = sq cm.

Rectangle has the largest area while rectangle has the smallest area.

What is the length of the wooden strip required to frame a photograph of length and breadth 32 cm and 21 cm respectively?

Length of the photograph = cm

Breadth of the photograph = cm

We need to find the to calculate the length of the wooden strip.

Perimeter = 2×(l+b) = 2×(32+21) = 2 × =  cm

Thus, the required length of the wooden strip is 106 cm.

What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of ₹8 per hundred sq m?

Instructions

Length of the rectangular plot = m
Breadth of the rectangular plot = m
∴ Area of the plot = l × b = 500 m × 200 m = sq m
Now rate of tiling the plot = ₹ per 100 sq m
Cost of tiling the garden = ₹( × 100000 ) = ₹
Hence the required cost = ₹8000

A table-top measures 2 m by 1 m 50 cm. What is its area in square metres?

Instructions

Length of the table-top = m
Breadth = m cm = m
∴ Area of the table-top = l × b = 2 m x 1.50 m = sq m
Hence, the area of table-top = 3 sq m.

A room is 4 m long and 3 m 50 cm wide. How many square metres of carpet is needed to cover the floor of the room?

Length of the room = m

Breadth = 3 m 50 cm = m

Area of the room = l × b = 4 m × 3.5 m = sq m

Hence, the area of the carpet needed = 14 sq m

A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.

Length of the floor = m , breadth = m

Area of the floor = length × breadth = 5 × 4 = sq m

Side of the carpet = m

Area of the square carpet = side × side = 3 × 3 = sq m

Area of the floor which is not carpeted = sq m – sq m = sq m.

Five square flower beds each of sides 1 m are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of the land?

Instructions

Side of the square flower bed = m.
Area of 1 square flower bed = m × m = sq m.
Area of 5 square flower beds = 1 sq m × = sq m.
Now length of the land = m , breadth = m
Area of the land = length × breadth = 5 m × 4 m = sq m
Area of the remaining part of the land = sq m – sq m = sq m.

By splitting the following figures into rectangles, find their areas (The measures are given in centimetres).

Area of the rectangle =
Area of the rectangle I = cm × cm = sq cm
Area of the rectangle II = cm × cm = sq cm
Area of the rectangle III = cm × cm = sq cm
Area of the rectangle IV = cm × cm = sq cm
Total area of the whole figure = 12 sq cm + 6 sq cm + 4 sq cm + 9 sq cm = sq cm.
Area of the rectangle I = cm × cm = sq cm
Area of the rectangle II = cm × cm = sq cm
Area of rectangle III = cm × cm = sq cm
Total area of the given figure = 3 sq cm + 3 sq cm + 3 sq cm = sq cm.

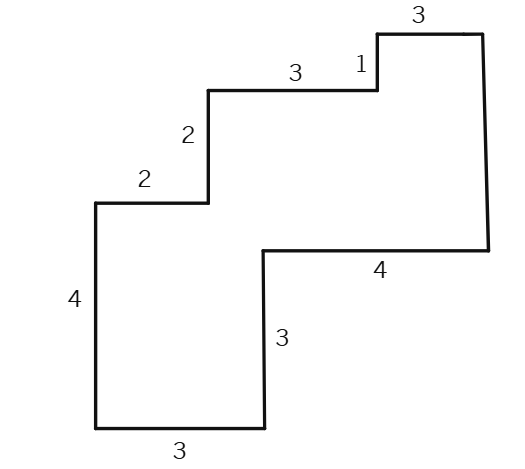
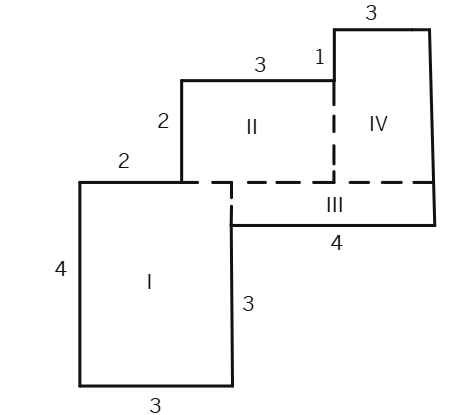
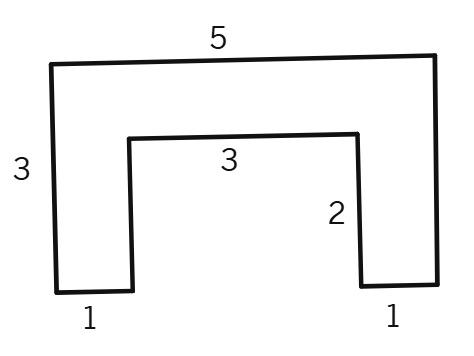
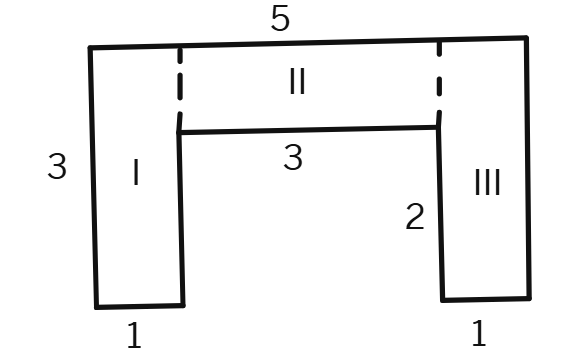
Split the following shapes into rectangles and find their areas. (The measures are given in centimetres)

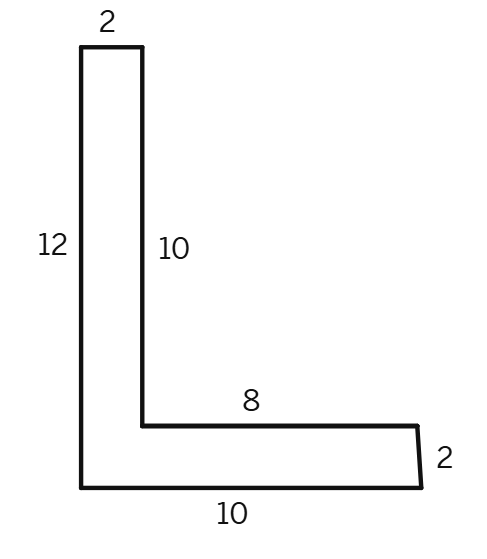
(a)

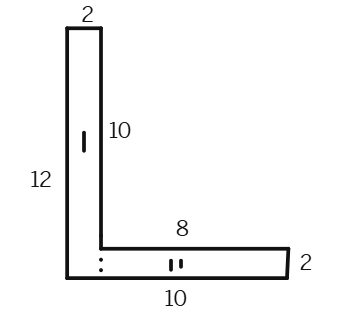
Area of the rectangle I = 12 cm × cm = sq cm

Area of the rectangle II = cm × 2 cm = sq cm

Total area of the whole figure = sq cm + sq cm = sq cm.

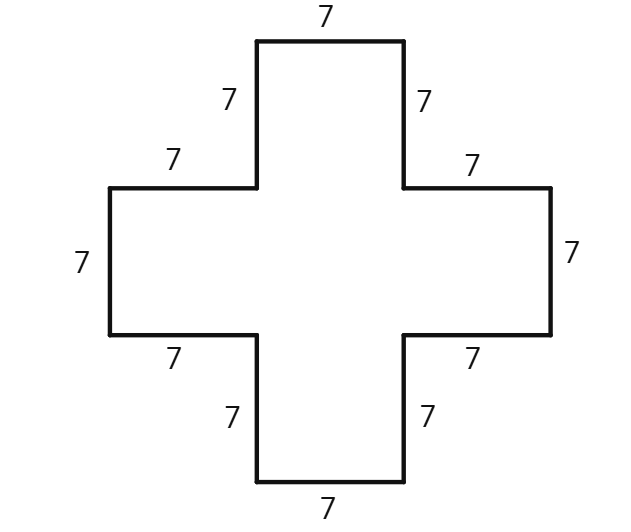
(b)

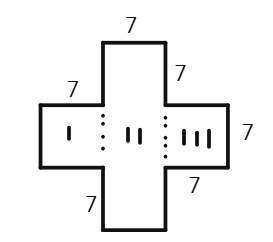
Area of the rectangle I = cm × 7 cm = sq cm

Area of the rectangle II = cm × 7 cm = sq cm

Area of the rectangle III = 7 cm × cm = sq cm

Total area of the whole figure = 49 sq cm + 147 sq cm + 49 sq cm = sq cm.

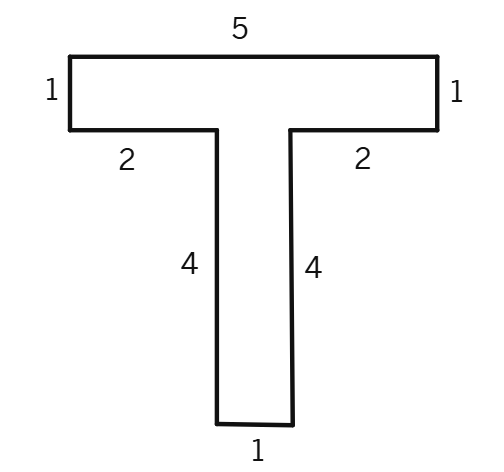
(c)

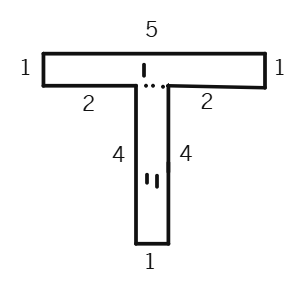
Area of the rectangle I = cm × cm = sq cm

Area of the rectangle II = cm × 1 cm = sq cm

Total area of the whole figure = 5 sq cm + 4 sq cm = sq cm.

How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed to fit in a rectangular region whose length and breadth are respectively.

Length of one tile = cm

Breadth of the tile = cm

Area of 1 tile = length × breadth = 12 cm × 5 cm = sq cm

(a) 100 cm and 144 cm

Length of the rectangular region = cm
Breadth of the region = cm
Area of the rectangular region = length × breadth = 144 cm × 100 cm = sq cm
Number of tiles needed to cover the whole rectangular region = 14400 sq cm ÷ 60 sq cm = tiles

(b) 70 cm and 36 cm.

Length of the rectangular region = cm
Breadth of the region = cm
Area of the rectangular region = length × breadth = 70 cm × 36 cm = sq cm
Number of tiles needed to cover the whole rectangular region = 2520 sq cm ÷ 60 sq cm = tiles.