Enhanced Curriculum Support

Sec A

1. The value of 25−2 is:

(a) 425 (b) 52 (c) 45 (d) 254

2. If 3x+8 = 272x+1 then the value of x will be:

(a) 1 (b) -2 (c) 7 (d) 3

3. Simplify: −32 × 532

(a) 4 (b) 27 (c) 25 (d) 8

4. The value of 0.00006456 is:

(a) 32100000 (b) 1610000 (c) 3210000 (d) 16100000

5. The value of 122+5212 is:

(a) 13 (b) 11 (c) 15 (d) 12

6. The standard form for 234000000 is:

(a) 0.234×10−9 (b) 2.34×108 (c) 2.34×10−8 (d) 0.234×109

7. The value of px×py÷px÷py is:

(a) p2y (b) 2px (c) 2py (d) p2x

8. If 3x = 19 , the value of x is:

(a) 1 (b)-2 (c) 2 (d) 12

9. x−3y323×x3y−3−23 is equal to:

(a) 1x2y2 (b) y4x−4 (c) x4y−4 (d) x−4y4

Sec B

1. Find the value of x, so that −23 × −2−6 = −22x−1

(OR)

Simplify and write in exponential form: −2−3 × −2−4

2. Find the value of x in the expression 2x+2x+2x = 192

3. Express 0.000045 in scientific notation.

4. Express 1.25 × 106 + 3.45 × 105 in standard form.

5. Write 2−3 as a fraction and evaluate.

Sec C

1. Add p3−1 , p3+p+2 and p2−2p+1.

2. Find the value of : 12−2 + 13−2 + 14−2

3. Express in standard form: 2years in seconds

(OR)

The diameter of the Sun is 1.4×109 m and the diameter of the Earth is 1.2756×107 m. Compare their diameters by division.

4. A light-year is a distance that light can travel in one year. 1 light year = 9,460,000,000,000 km. a. Express one light-year in scientific notation. b. The average distance between Earth and Sun is 1.496×108 km. Is the distance between Earth and the Sun greater than, less than or equal to one light-year?

5. Find the volume of rectangular box with sides are 4p2q3, 3pq and 2p2q

(OR)

Find the sum of 4x2−3x+2 and 3x2+4x−8.

6. If a = 102 , b =10−3, find a⋅b and ab.

Sec D

1. Find the product of 12p3q6−23p4qpq2

2. Suppose 2 kg of sugar contains 9×106 crystals. How many sugar crystals are there in (i) 5 kg of sugar ? (ii) 1.2 kg of sugar ?

3. Simplify: 3−5×10−5×1255−7×6−5

(OR)

Simplify: 67−1−16−1−1 ÷ 29−1

4. Solve 2x⋅ 32 = 108, and find the value of x.

5. Convert 2.34 × 105 . 4.56 × 103 to decimal and back to standard form.

Problem 1

The population of a city is 1×106. If the population grows by 2% every year, express the population after 5 years using exponents. How does rapid population growth impact resources, and what can individuals do to ensure sustainable growth and responsible usage of resources?

Problem 2

In a hypothetical scenario, a contagious disease spreads at an exponential rate, with each infected person spreading the disease to 3 others every day. If there are initially 5 infected individuals, how many people will be infected after 5 days? Discuss how vaccination and following safety measures can prevent exponential disease spread and protect public health.

Problem 3

The energy consumption of a household over a year is approximately 1×105 kilowatt-hours. If every household in a town of 104 homes reduced their energy consumption by 10%, how much total energy would be saved in the town in a year? Discuss the importance of energy conservation and how even small reductions can have a large impact.

Q1

Prove that a0 = 1 for any non-zero a using the properties of exponents. Additionally, explain why a−1 equals 1a using a real-world example involving fractions or rates.

Q2

Which is larger, 210 or 55 ? Without calculating the exact values, explain how you can estimate which one is greater using properties of exponents.

Q3

A population of bacteria doubles every 4 hours. If the initial population is 500, express the population P(t) after t hours as a function of t using exponents. How many bacteria will there be after 24 hours?

Q4

If 2x×3yz = 36, find the values of x, y, and z that satisfy the equation. Is it possible to have more than one solution? Explain why or why not.

Questions

1. Multiplicative inverse of 27 is:

(a) 2−7 (b) 72 (c) −27 (d) 27

2. True/False: Very small numbers can be expressed in standard form using positive exponents.

3. True/False: (–10) × (–10) × (–10) × (–10) = 10−4

4. The distance between earth and sun is 150 million kilometres which can be written in exponential form as ?

5. 2−32×3−23 = ?

6. Find x so that −5x+1 × −55 = −57

7. Simplify: −23×−273×46

8. For a fixed base, if the exponent decreases by 1, the number becomes:

(a) One-tenth of the previous number.

(b) Ten times of the previous number.

(c) Hundredth of the previous number.

(d) Hundred times of the previous number.

9. A new born bear weighs 4 kg. How many kilograms might a five year old bear weigh if its weight increases by the power of 2 in 5 years?

10. In 2n, n is known as:

(a) Base (b) Constant (c) x (d) Variable

11. The value of −234 is equal to:

(a) 1681 (b) 8116 (c) −1681 (d) −8116

12. If x be any integer different from zero and m be any positive integer, then x−m is equal to:

(a) xm (b) −xm (c) 1xm (d) −1xm

13. An insect is on the 0 point of a number line, hopping towards 1. She covers half the distance from her current location to 1 with each hop. So, she will be at 12 after one hop, 34 after two hops, and so on.

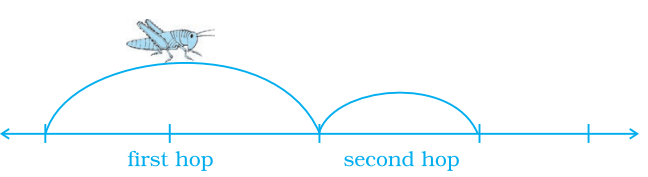
(a) Make a table showing the insect’s location for the first 10 hops.

(b) Where will the insect be after n hops?

(c) Will the insect ever get to 1? Explain.

14. By what number should −32−3 be divided so that the quotient may be 427−2?

15. Some migratory birds travel as much as 15,000 km to escape the extreme climatic conditions at home. Write the distance in metres using scientific notation.

16. Express each of the following in standard form:

(a) The mass of a proton in gram is 16731e+27

(b) A Helium atom has a diameter of 0.000000022 cm.

(c) Mass of a molecule of hydrogen gas is about 0.00000000000000000000334 tons.

(d) Human body has 1 trillon of cells which vary in shapes and sizes.

(e) Express 56 km in m.

(f) Express 5 tons in g.

(g) Express 2 years in seconds.

(h) Express 5 hectares in cm^2 (1 hectare = 10000 m2)

17. Express 1.5×1062.5×10−4 in the standard form.

18. Express the product of 3.2×106 and 4.1×10−1 in the standard form.

19. Find the multiplicative inverse of −7−2 ÷ 90−1.

20. By what number should we multiply −290 so that the product becomes +290.

21. Express 2764 and −2764 as powers of a rational number.

22. The value of [1−2 + 2−2 + 3−2] × 62 is : ?

Q1

Prefixes which are used to represent large or very small numbers

Distance between different places and objects

(1) (i) Usually, the prefix used with metre to represent the distance between two cities is 'kilo'. If you have to choose another prefix for metre to represent the distance between Delhi and Washington, D. C., which of the following prefixes are most suitable? Choose any two.

(a) Tera (b) Mega (c) Micro (d) Giga

(ii) Distance between the Sun and Earth is how many gigametres?

(2) If you have to choose a prefix for metre to represent the distances given in i and ii below, such that the number representing the distance satisfies the following conditions, which prefixes will you choose?

Condition:

If the number is greater than one (>1) then there can be either two or only one digit to the left of the decimal point, e.g.: 2.75, 45.58, but not 134.84. If the number is less than one (<1) then the digit at the immediate right of the decimal point should not be zero, e.g.: 0.125, 0.5, but not 0.015.

E.g., the distance between the Sun and the Earth is given as 1.5118x1011 metres, i.e., 1.5118x1011metres = 0.15118x1012 metres = 0.15118(number) terametres(prefix).

(i) Distance between Bengaluru and Delhi.

(ii) Distance between the Earth and Moon

(3) The diameter of the human hair varies from 0.000017 metres to 0.00018 metres. Express these numbers using a suitable unit with a prefix satisfying the condition given in Question 2.

Sol 1

Solution:

(1) (i) Option (b) and (d)

(ii) The distance between the Sun and Earth is 151.18 gigametres.

(2) (i) The appropriate prefix is Mega (Mm).

(ii) The appropriate prefix is Giga (Gm).

(3) The diameter of human hair varies from 17 micrometres (µm) to 180 micrometres (µm).

Q2

Have you ever wondered which is the smallest object around you? If you zoom in on any object around, you can see them in greater detail, with smaller and smaller features being visible. But you can’t zoom in beyond a certain point because of our eyes/camera limitations. If we use the most advanced devices we see that the smallest unit from which all the objects are made is an atom. We can imagine an atom to have a spherical shape with a diameter in the range of 10−10 m.

Similarly, if you ask which is the single largest distinct object in the universe, the answer is a galaxy. The galaxy typically contains many stars. Our planet exists in a galaxy called the Milky Way, whose shape is a spiral, as shown in the figure, with a diameter of 1021 m.

(1) (i) 10−10 m is known as one Angstrom (Å). A distance of 1 kilometre is how many angstroms?

(ii) If you place atoms side by side to form a long line, how many atoms will you need to cover the entire diameter of the Milky Way galaxy? Assume that the atoms have the size mentioned in above.

(2) (i) Planet Earth is also spherical in shape with a diameter of 12,742,000 metres. We can say that the diameter of an atom is ? times smaller than the diameter of the Earth. Choose the closest answer.

(a) 1.3 x 10−18 (b) 1.2 x 1010

(c) 1.2 x 10−19 (d) 1.3 x 1017

(ii) The diameter of the Milky Way galaxy is how many times larger than the diameter of the Earth? Choose the closest answer.

(a) 1012 (b) 1014

(c) 1017 (d) 1019

Sol 2

Solution:

(1) (i) 1 kilometre = 1013 A.

(ii) 1031 atoms are required to cover the entire diameter of the Milky Way.

(2) (i) Option (a)

(ii) Option (b)