Exercise 6.1
We have two lines AB and CD intersecting at O. If ∠ AOC + ∠ BOE = 70° and ∠ BOD = 40°, find:
∠ BOE and reflex ∠ COE
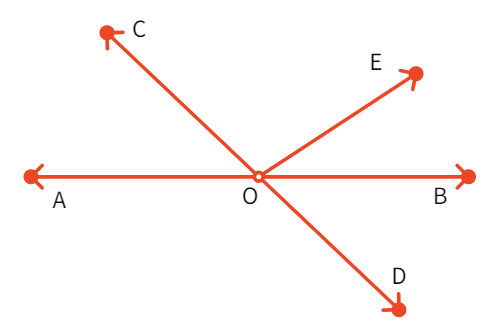
- We see: ∠ AOC + ∠ BOE + ∠ COE =
° and ∠COE + ∠BOD + ∠BOE is to it. - Substituting the given values in the two equations separately.
- We get ∠COE =
°. Thus, reflex of ∠ COE = ° - We also see: ∠BOE =
° - We have found the answer
Lines XY and MN intersect at O. If ∠ POY = 90° and a : b = 2 : 3, find c.
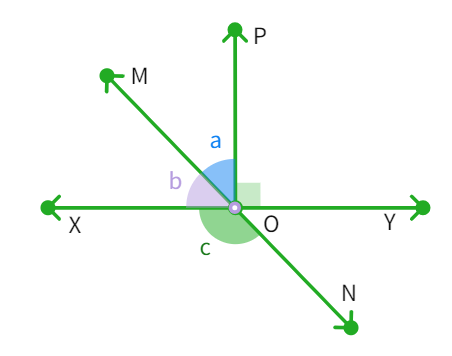
- We have ∠POY + a + b =
° where ∠POY = ° - Thus, we get a + b = 90°
- If a = 2x, we get b =
which gives x = ° - Thus, a =
° and b = ° - We see that c and b form a linear pair: c =
° - We have found the answer
In the below figure if ∠ PQR = ∠ PRQ, then prove that ∠ PQS = ∠ PRT.
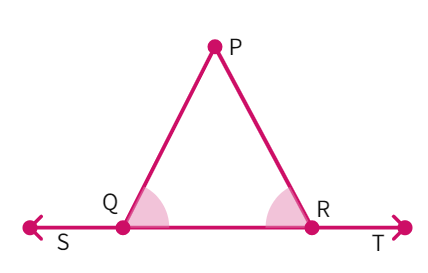
- We see that ∠PQS + ∠PQR =
° and ∠PRT + ∠PRQ = ° - We have also been given that: ∠PQR = ∠PRQ
- Thus, we get ∠PQS = ∠
- We have found the answer
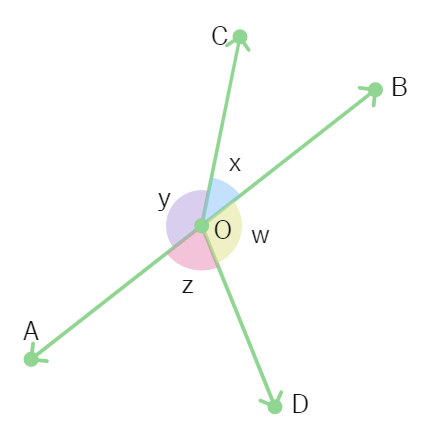
In the figure, if x + y = w + z, then prove that AOB is a line.
Find the values
Solution: To prove AOB is a straight line, we will have to prove x + y is a x + y =
We know that the angles around a point are x + y + w + z =
Given: x+y = w+z. So, (x+y)+(x+y) =
⇒
Thus, AOB is a straight line.
PQ is a line with ray OR perpendicular to it at point O. OS is another ray lying between rays OP and OR. Prove that ∠ ROS =
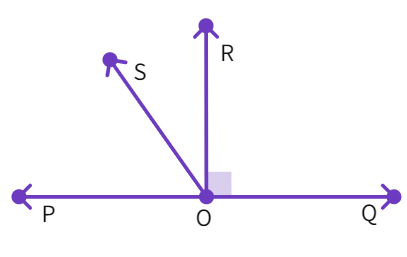
- Given: ∠ROP = ∠ROQ =
° and ∠POQ = ° - We also see: ∠POS + ∠
= ∠ROQ - Which can also be written : ∠POS + ∠ROS = ∠
– ∠ - Which further gives:
∠ROS = ∠QOS – ∠POS - Finally: ∠ROS =
(∠QOS – ∠POS) - We have found the answer
It is given that ∠ XYZ = 64° and XY is produced to point P. If ray YQ bisects ∠ ZYP, find ∠ XYQ and reflex ∠ QYP.
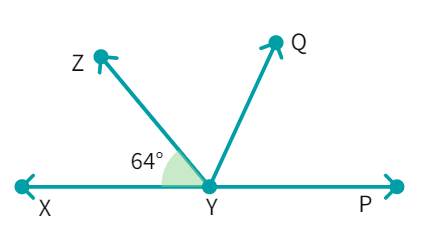
- Value of ∠ZYP =
° - As YQ bisects ∠ZYP: ∠ZYP = ∠ZYQ + ∠QYP =
∠ZYQ - Thus, ∠ZYQ =
° - From the figure: ∠XYQ = ∠XYZ + ∠ZYQ
- which gives ∠XYQ =
° - Therefore, reflex ∠QYP =
° + ∠XYQ = ° - We have found the answer