Innings2
Create New Account

Sign in to Innings2

or

New Account     Reset Password     

Chapter 6: Lines and Angles

    Introduction

    Basic Terms and Definitions

    Intersecting Lines and Non-intersecting Lines

    Pairs of Angles

    Lines Parallel to the Same Line

    Exercise 6.1

    Exercise 6.2

    Summary

    Enhanced Curriculum Support

Powered by Innings 2

Reset Progress

This will delete your progress and chat data for all chapters in this course, and cannot be undone!

Glossary

Select one of the keywords on the left…

Chapter 6: Lines and Angles > Exercise 6.2

Exercise 6.2

If AB || CD, CD || EF and y : z = 3 : 7, find the value of x.

Instructions

Observe the above figure

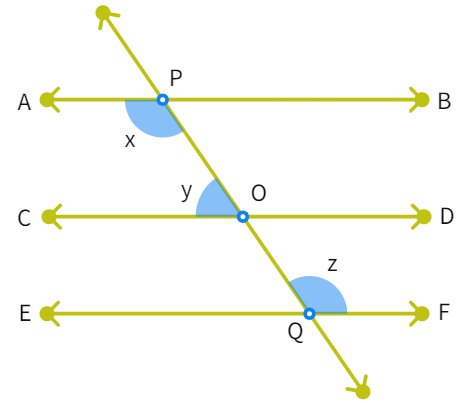
  • x and y are angles on the same side of the transversal: x + y = °
  • We also have ∠POD = - (1) as they are corresponding angles.
  • and y + ∠POD = ° - (2) as a linear pair
  • (1) and (2) gives us: + = 180°
  • Since, y : z = 3 : 7 we can write 3w + 7w = 180° which gives us w = °
  • Upon solving for values using the equations, we get: x = ° , y = ° and z = °
  • We have found the answer

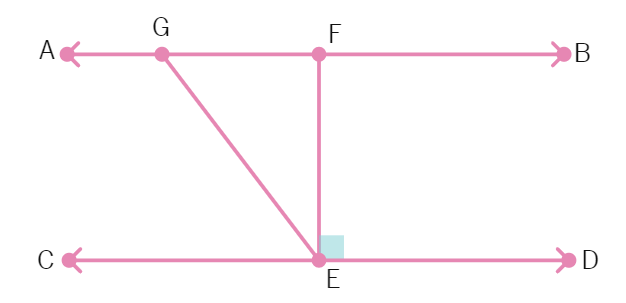
In the given figure, if AB || CD, EF ⊥ CD and ∠ GED = 126°, find ∠ AGE, ∠ GEF and ∠ FGE.

Question 2 Figure

Instructions

Solution: Since AB || CD, GE is a . Given that ∠GED = 126°. So, ∠GED = ∠AGE = ° as they are angles.
Also we have: ∠GED = ∠GEF + ∠ . As EF ⊥ CD, ∠ FED = °
Thus, ∠GED = ∠GEF + 90° i.e. ∠GEF = ° – ° = °
⇒ Again we have, ∠FGE + ∠GED = °
Putting the value of ∠GED = 126°, we get ∠FGE = °
We have found all the answers.

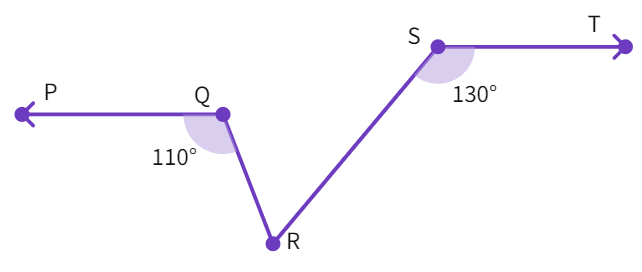
In the figure, if PQ || ST with ∠ PQR = 110° and ∠ RST = 130°, find the value of ∠ QRS.

Lets's construct a line XY parallel to PQ. Now, consider the below figure-

Draw a parallel line through R

Instructions

Observe the above figure with the construction

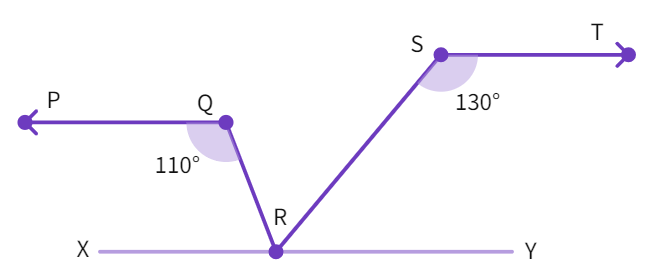
  • As angles on the same side of the transversal: ∠PQR + ∠ = 180°
  • This gives ∠QRX = °
  • Similarly, ∠RST + ∠ = 180°
  • Giving ∠SRY = °
  • From the figure, ∠ + ∠QRS + ∠SRY = 180°
  • Upon solving, we get: ∠QRS = °
  • We have found the answer

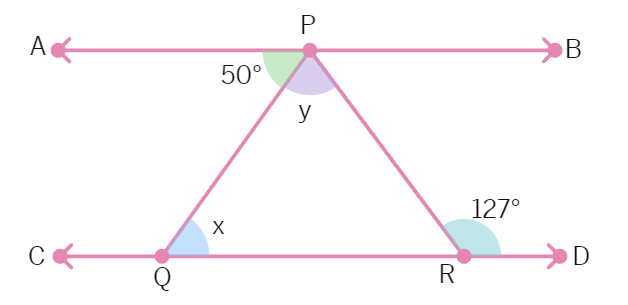
In the figure, if AB || CD, ∠ APQ = 50° and ∠ PRD = 127°, find x and y.

Instructions

Solution: From the diagram, ∠APQ = ∠ as they are angles.
Now, putting the value of ∠APQ = 50° and ∠PQR = x, we get x = °
Also, ∠APR = ∠ as they are angles which gives us ∠APR = °
We know that ∠APR = ∠APQ + ∠. Putting values of ∠QPR = y and ∠APR = 127°, we get: ° = °+ y ⇒ y = °
Thus, the values of x and y are calculated as: x = 50° and y = 77°

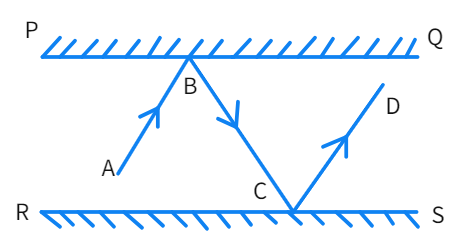
PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Is AB || CD ?

First, draw two perpendiculars BE and CF, such that BE ⊥ PQ and CF ⊥ RS.

Since PQ || RS, BE || CF as well.

Draw perpendiculars from point of incidence.

Instructions

Observe the above figure with the construction

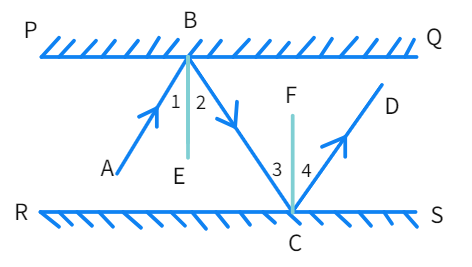
  • As Angle of incidence = Angle of reflection, we get: ∠1 = ∠ and ∠ = ∠4
  • We also have BE || CF with BC acting as a transverse: ∠2 = ∠
  • Since, ∠2 and ∠3 are also equal
  • We can further say the above
  • Which gives ∠ABC = ∠
  • As the alternate interior angles are equal, we can conclude.