Lines Parallel to the Same Line
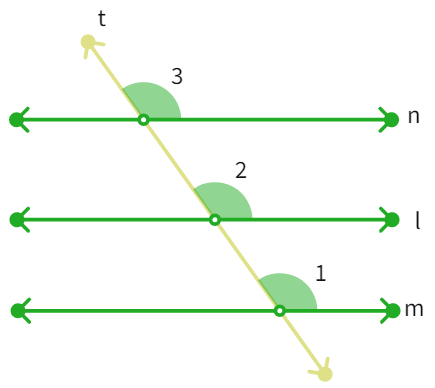
If two lines are parallel to the same line, are the two lines parallel to each other? In the above figure:
line m || line l and
line n || line l.
If we draw a transversal line t for the parallel lines, we already know that:
∠ 1 = ∠
So, ∠ 1 = ∠
Since, ∠ 1 and ∠ 3 are the corresponding angles for the parallel lines m and n, we can therefore, say that:
Line m || Line n (Converse of corresponding angles axiom)
Thus, we can state this in the form of the following theorem:
Theorem : Lines which are parallel to the same line are parallel to each other.
Given the same reasoning, this property can be extended to more than
Example 4: In the figure, if PQ || RS, ∠ MXQ = 135° and ∠ MYR = 40°, ∠ XMY will be equal to:
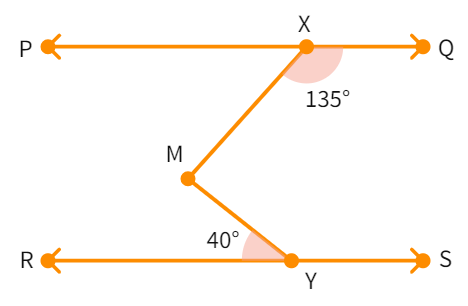
First construct a line AB parallel to line PQ and passing through point M.

Now, AB ||
AB ||
- Now, ∠ QXM + ∠ XMB =
° and ∠ QXM = 135° - Thus, ∠ XMB = 45° (1)
- We also know ∠ BMY = ∠ MYR as they are
angles - Thus, ∠ BMY =
° (2) - Upon adding (1) and (2) we get : ∠ XMY = ∠
+ ∠ - So, ∠ XMY =
° + ° = ° - We have found the answer
Example 5: If a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel.
Let's take the following: PQ and RS are two lines with a transversal AD as shown. The corresponding angles ∠ ABQ and ∠ BCS have angle bisectors BE and CG, respectively which are parallel to each other.
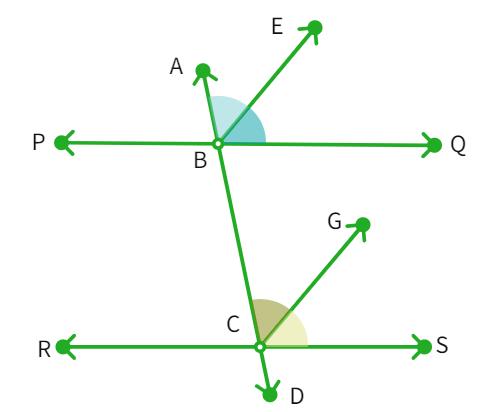
- Since, ray BE and CG are bisectors of ∠ ABQ and ∠ BCS.
- Thus, ∠ ABE =
∠ ABQ and ∠ BCG = ∠ BCS - We can also see that BE || CG and AD is the
. - ∠ ABE = ∠ BCG are
angles - Putting (1) and (2) in (3) we get
- As the
angles formed by transversal AD with PQ and RS are : PQ || RS
Example 6: In the figure, AB || CD, CD || EF and EA ⊥ AB. If ∠ BEF = 55°, find the values of x, y and z.
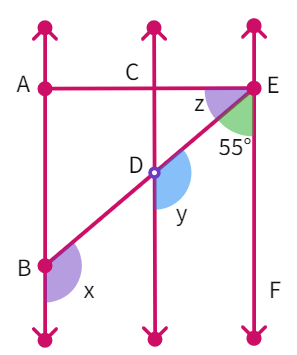
- We see that y + 55° = 180° as they are
angles on the same side of the transversal. - Thus, y =
° - We also have y =
as they are angles - Which gives us x =
° - We have been given that ∠ EAB =
° - So, ∠ EAB + ∠
= 180° which gives z = ° - We found all the answers.
