Enhanced Curriculum Support

Sec A

(1) An icecream cone has hemispherical top. If the height of the cone is 9 cm and base radius is 2.5 cm, then the volume of icecream is:

(a) 91.67 cm3 (b) 96.67 cm3

(c) 90.67 cm3 (d) 91.76 cm3

(2) The curved surface area of a cylinder and a cone is equal. If their base radius is same, then the ratio of the slant height of the cone to the height of the cylinder is:

(a) 1 : 1 (b) 2 : 3

(c) 1 : 2 (d) 2 : 1

Sec B

(1) The radii of two cones are in the ratio 2 : 1 and their volumes are equal. What is the ratio of their heights?

(OR)

A hollow spherical shell is made of a metal of density 4.5 g per cm3. If its internal and external radii are 8 cm and 9 cm respectively, find the weight of the shell.

(2) The outer diameter of a spherical shell is 10 cm and the inner diameter is 9 cm. Find the volume of the metal contained in the shell.

(3) Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find the radius of the base.

(OR)

If the radius and slant height of a cone are in the ratio 7 : 13 and its curved surface area is 286 cm2, find its radius.

(4) If the volume of a right circular cone of height 9 cm is 48 cm3, find the diameter of its base.

(OR)

A team of 10 interns and 1 professor from zoological department visited a forest, where they set up a conical tent for their accommodation. There they perform activities like planting saplings, yoga, cleaning lakes, testing the water for contaminants and pollutant levels and desilt the lake bed and also using the silt to strengthen bunds. Find the radius and height of the tent if the base area of tent is 154 cm2 and curved surface area of the tent is 396 cm2.

Sec C

(1) Vinod and Basant have an adventure tourism business in Rishikesh. They have a resort in Rishikesh but now they are planning to build some tent houses too. The newly built tent house will have all the basic amenities and it will attract the young tourists coming for adventure. Their conical tent is 9 m high and the radius of its base is 12 m.

(i) What is the cost of the canvas required to make it, if 1 m2 canvas costs ₹ 10?

(ii) How many persons can be accommodated in the tent, if each person requires 2 m2 on the ground?

(iii) How many persons can be accommodated in the tent, if each person requires 15 m3 of space to breathe in?

(OR)

If each person requires 20 m3 of space to breathe in and 100 person can be accommodated then what should be height of tent?

(2) A golf ball is spherical with about 300 - 500 dimples that help increase its velocity while in play. Golf balls are traditionally white but available in colours also. In the given figure, a golf ball has diameter 4.2 cm and the surface has 315 dimples (hemi-spherical) of radius 2 mm.

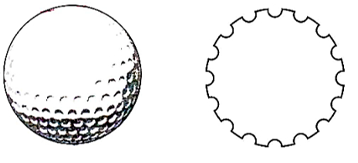
(i) Find the surface area of one such dimple. (1)

(ii) Find the volume of the material dug out to make one dimple. (1)

(iii) Find the total surface area exposed to the surroundings. (2)

(OR)

Find the volume of the golf ball. (2)

(3) A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and a height of 1 m.

(i) Find the curved surface area of the cone.

(ii) If the outer side of each of the cones is to be painted and the cost of painting is ₹ 12 per m2, what will be the cost of painting all these cones? (Use π = 3.14 and take 1.04 = 1.02)

Sec D

(1) What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m?Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm. (Use π = 3.14)

(2) An iron pillar consists of a cylindrical portion 2.8 m high and 20 cm in diameter and a cone 42 cm high is surmounting it. Find the weight of the pillar, given that 1 cm3 of iron weighs 7.5 g.

Problem 1

A factory is planning to use cylindrical containers for recycling waste materials. Each container has a height of 2 m and a radius of 1 m. The factory intends to buy 50 such containers. Calculate the total surface area of one container. Discuss how recycling can help reduce environmental pollution and the importance of responsible waste management.

Problem 2

A school is installing a hemispherical dome over their new auditorium. The radius of the dome is 7 m. Find the surface area of the dome. How can architectural designs like domes help save materials and energy? Discuss the importance of sustainable construction practices in today’s world.

Problem 3

A group of students decides to paint a spherical water tank to beautify their village. The tank has a radius of 4.2 m. If 1 liter of paint covers 10 m², how much paint will they need to cover the entire surface of the tank? How can such community service activities foster a sense of responsibility and teamwork among students?

Q1

A solid toy is in the shape of a hemisphere surmounted by a right circular cone. The radius of the hemisphere is 3 cm, and the height of the cone is 6 cm. Calculate the total surface area and volume of the toy. If the toy is dipped halfway into paint, how much of the surface area will be painted?

Q2

You have a sheet of metal measuring 60 cm by 80 cm. You need to create an open-top rectangular box by cutting equal squares from each corner and folding up the edges. What size of the squares should be cut to maximize the volume of the box? How do the surface area and volume change as the size of the square changes?

Q3

A cylindrical can and a cube-shaped box have the same surface area. If the height of the cylindrical can is 10 cm and its radius is 5 cm, compare the volume of the can to the volume of the cube. Which shape provides more storage capacity and why? Can you generalize a rule for other shapes with the same surface area?

Q4

A milkman uses a conical vessel to measure milk. The radius of the base is 4 cm, and the height is 10 cm. He then pours the milk into a cylindrical vessel with the same radius and height of 8 cm. Does the conical vessel hold more or less milk than the cylindrical vessel? How does the shape of the container impact the efficiency of the milkman’s work, and can you suggest an optimal design?

Questions

(1) In a cylinder, if radius is halved and height is doubled, the volume will be:

(A) same (B) doubled (C) halved (D) four times

(2) The total surface area of a cube is 96 cm2. The volume of the cube is:

(A) 8 cm3 (B) 512 cm3 (C) 64 cm3 (D) 27 cm3

(3) The radii of two cylinders are in the ratio of 2:3 and their heights are in the ratio of 5:3. The ratio of their volumes is:

(A) 10 : 17 (B) 20 : 27 (C) 17 : 27 (D) 20 : 37

(4) The number of planks of dimensions (4 m × 50 cm × 20 cm) that can be stored in a pit which is 16 m long, 12m wide and 4 m deep is:

(A) 1900 (B) 1920 (C) 1800 (D) 1840

(5) The radius of a hemispherical balloon increases from 6 cm to 12 cm as air is being pumped into it. The ratios of the surface areas of the balloon in the two cases is:

(A) 1 : 4 (B) 1 : 3 (C) 2 : 3 (D) 2 : 1

Questions

(1) A right circular cylinder just encloses a sphere of radius r. The surface area of the sphere is equal to the curved surface area of the cylinder.

(2) An edge of a cube measures r cm. If the largest possible right circular cone is cut out of this cube, then the volume of the cone (in cm3) is 16πr3.

(3) A cylinder and a right circular cone are having the same base and same height. The volume of the cylinder is three times the volume of the cone.

(4) If a sphere is inscribed in a cube, then the ratio of the volume of the cube to the volume of the sphere will be 6 : π.

(5) A cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their volumes is 1 : 2 : 3.

Questions

(1) The surface area of a sphere of radius 5 cm is five times the area of the curved surface of a cone of radius 4 cm. Find the height and the volume of the cone (taking π = 227).

(2) The radius of a sphere is increased by 10%. Prove that the volume will be increased by 33.1% approximately.

(3) A storage tank is in the form of a cube. When it is full of water, the volume of water is 15.625 m3. If the present depth of water is 1.3 m, find the volume of water already used from the tank.

(4) A small village, having a population of 5000, requires 75 litres of water per head per day. The village has got an overhead tank of measurement 40 m × 25 m × 15 m. For how many days will the water of this tank last?

(5) Rain water which falls on a flat rectangular surface of length 6 m and breadth 4 m is transferred into a cylindrical vessel of internal radius 20 cm. What will be the height of water in the cylindrical vessel if the rain fall is 1 cm. Give your answer to the nearest integer. (Take π = 3.14)

(6) 30 circular plates, each of radius 14 cm and thickness 3cm are placed one above the another to form a cylindrical solid. Find:

(i) the total surface area

(ii) volume of the cylinder so formed

Q1

Vittal runs a small refreshment store in which he sells buns, coffee, tea and a special type of fruit juice. His juice dispenser is of cuboidal shape. The base has an area of 500 cm2 and the height of the dispenser is 25 cm. Every morning he prepares this juice using water and concentrated fruit syrup in the ratio of 3:1. He uses 2.5 litres of fruit syrup daily (1 litre = 1000 cm3).

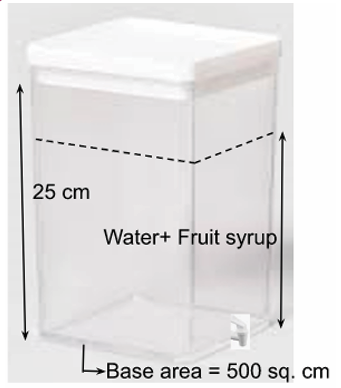
1. Once the juice is made, how much of the dispenser will be filled?

(a) 75% (b) 85%

(c) 80% (d) 90%

2. As the consumption of juice increases during summer, Vittal fills his juice dispenser to its maximum capacity. How much fruit syrup is used to prepare a dispenser full of juice?

3. Vittal introduced a token/coin operated juice dispenser. The customer gets a token and an empty glass from Vittal after paying the requisite amount, which when inserted in the machine fills the glass. For the entire dispenser to get emptied, 60 coins are needed. What is the approximate volume of juice each cup will hold?

(a) Slightly more than 200 mL (b) Exact 200 mL

(c) Slightly less than 200 mL (d) Around 150 mL

Sol

(1) Solution: Option (c)

(2) Solution: Vittal uses 3.125 liters of fruit syrup to prepare a dispenser full of juice.

(3) Solution: Option (a)

Q2

One of the most popular puzzles globally, a Rubik’s cube is a 3x3x3 cu. unit cube, where each face is tiled with 9 identically coloured stickers. The 6 different faces, each with a different colour, can be mixed around by independently rotating each face of the cube. Once the colours are mixed, the challenge, of course, is to keep playing and make each face a single colour once again! As you can imagine, the combinations seem endless, and to the uninitiated, virtually impossible to solve!

However, its apparent simplicity keeps even the novice hooked. The mathematical nature of the puzzle allows one to make several conceptual connections with it: e.g. to study surface area, volume, ratios, fractions etc., as you yourself will do by answering several of the questions below.

Zara was playing with her 3 x 3 Rubik’s cube and it fell down from her hand and all the small cubes from which it was made fell apart. She rearranged them, but the central piece on the top surface was missing.

1. What will be the new surface area if each smaller cube is made from a cube of side 1 unit?

(a) 58 sq.units

(b) 57 sq.units

(c) 53 sq.units

(d) 54 sq.units

2. Which of the following is a correct statement with respect to the comparison among the non-broken cube and the broken cube (shown above)? Note that 1 cm3 = 1 ml.

(a) Both surface area and volume decrease.

(b) Both surface area and volume increase.

(c) Surface area increases but volume decreases.

(d) Surface area decreases but volume increases.

3. Knowing Zara’s love for her Rubik’s cube, her father gifted her a pen holder, which is in the shape of a Rubik’s cube from outside and cylindrical from inside, as shown below. By using a ruler and a thread, Zara measured the circumference of the circular opening portion of the pen holder as 22 cm. She also measured its depth as 7 cm.

To avoid the sharpened points of the pencil from breaking by coming in contact with the hard surface of the base, she decided to use a thin piece of foam for it and also pasted a colour paper layer on the inside of the cylindrical holder to make it more attractive.

(i) Find the area of the foam piece required. (π = 227)

(ii) What should be the area of the rectangular colour paper that can be used to cover the inner surface of the pen holder, without any wastage?

4. For her school craft exhibition, Zara prepared a scaled up static model of a Rubik’s cube, using thick cardboard (45 cm x 45 cm x 45 cm). She observed that each face of the Rubik's cube has multiple squares.

As seen below, she used square-shaped paper sheets (15 cm x 15 cm) of multiple colours. She covered all the faces of the cube except the base, since it won't be visible.

There was no overlapping or wastage while pasting and she drew thick black lines along the edges of the colour sheets. What is the total number of colour paper sheets she used for making this Rubik’s cube model?

Sol

(1) Solution: Option (c)

(2) Solution: Option (c)

(3) Solution: (i) The area of the foam piece required is 38.5 cm2.

(ii) The area of the rectangular color paper needed to cover the inner surface is 154 cm2.

(4) Solution: Zara used 45 colour paper sheets to cover the Rubik's cube model.

Q3

Fragrances of India, a famous perfume manufacturing company, sells its 3 perfumes in 3 different types of glass bottles, as shown below. The cost of the bottle is decided by the quantity and type of perfume it contains.

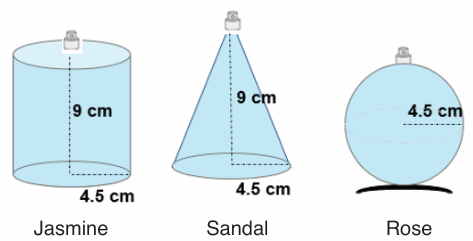
If all the bottles cost the same, which fragrance is the most expensive per unit volume? Choose the correct option which shows the price in increasing order.

(a) Rose, Jasmine, Sandal

(b) Sandal, Jasmine, Rose

(c) Jasmine, Sandal, Rose

(d) Jasmine, Rose, Sandal

For the data in Question 8, check the correctness of the assertion and reason.

Assertion (A): Without doing any calculation, we can arrange these bottles in the increasing order of cost per unit volume by comparing the relationship between their dimensions.

Reason (R): The base radius of all the three bottles is the same and the height is twice this radius for the cone and cylinder. So the cone will have one-third the volume of the cylinder; the sphere will have two-third the volume of the cylinder. Or, in other words, the cylinder’s volume will be three times that of the cone and 32 times that of the sphere.

(a) A and R are true and R is the correct reason for A.

(b) A is true, but R is the wrong reasoning for it.

(c) A is true and R is false.

(d) A is false; but R is the correct reasoning in itself.

The manufacturer is looking at having different shaped bottles, but with the same volume. He decided to change the dimensions of the cone and the cylinder shaped bottles shown above, so that all the three will have the same volume. The vendor who supplies these bottles comes with four proposals, which he can implement to alter the size of the bottles while manufacturing the bottles.

Solution 1: Double the height of the cone keeping the same radius.

Solution 2: Decrease the height of the cylinder to two-third of its height, keeping the same radius.

Solution 3: Double the base radius of the cone without changing its height.

Solution 4: Double the base radius of the cylinder without changing its height.

Which of the above solutions should be undertaken, individually or together, to match the requirement that all three will have the same volume?

(a) Both solution 2 and solution 3

(b) Both solution 1 and solution 3

(c) Both solution 1 and solution 2

(d) Only solution 3

Sol

(1) Solution: Option (c)

(2) Solution: Option (a)

(3) Solution: Option (c)