Exercise 7.3
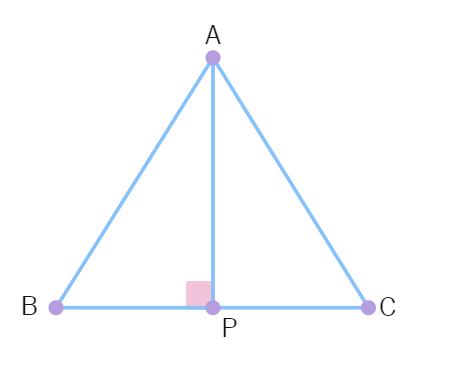
1.∆ ABC and ∆ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
(i) ∆ ABD ≅ ∆ ACD
(ii) ∆ ABP ≅ ∆ ACP
(iii) AP bisects ∠ A as well as ∠ D
(iv) AP is the perpendicular bisector of BC
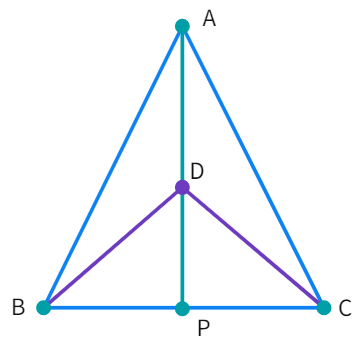
- Considering ΔABD and ΔACD we get: AD =
, AB = and BD = - Thus, by
congruency rule: ΔABD ≅ Δ - By CPCT: ∠BAD = ∠
- Considering ΔABP and ΔACP we get: AP =
, ∠PAB = ∠ and AB = - Thus, by
congruency rule: ΔABP ≅ Δ - By CPCT: BP =
- We already know that: ∠PAB = ∠
i.e. bisects ∠A — (i) - Considering the triangles ΔBPD and ΔCPD: PD =
, BD = and BP = . - Thus, by
congruency rule: ΔBPD ≅ Δ - By CPCT: ∠BDP = ∠
— (ii) and ∠BPD = ∠ - Comparing (i) and (ii) we get that
bisects ∠A as well as ∠D. - We already know: ∠BPD = ∠
and BP = (1) - We have: ∠BPD + ∠CPD =
° (As is a straight line) - Further on:
∠BPD = 180° which gives us - ∠BPD = ° (2) - From equations (1) and (2): AP is the perpendicular bisector of BC.
2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that:
(i) AD bisects BC (ii) AD bisects ∠ A
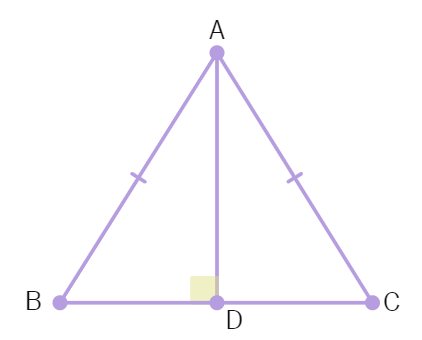
Solution:
3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ∆ PQR. Show that:
(i) ∆ ABM ≅ ∆ PQN
(ii) ∆ ABC ≅ ∆ PQR
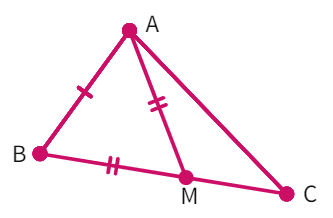
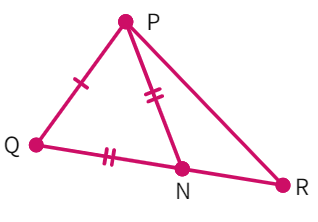
- Given: AB =
, BC = and AM = - We have:
1 2 and 1 2 (as AM and PN are (s)) - Also as BC = QR we get: BM =
- Considering the triangles ΔABM and ΔPQN: AM =
, AB = PQ, BM = - By
congruency: ΔABM ≅ Δ - By CPCT: ∠ABC = ∠
- Considering ΔABC and ΔPQR: AB =
, BC = and ∠ABC = ∠ - By
congruency: ΔABC ≅ Δ - Hence, proved.
4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
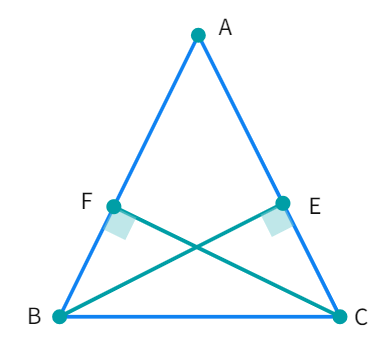
- Given: BE and CF are two
altitudes. - Considering the triangles ΔBEC and ΔCFB: ∠BEC = ∠CFB =
°, BC = CB (common) and BE = - By
congruence criterion: ΔBEC ≅ Δ - By CPCT: ∠C = ∠
- Therefore, AB =
as sides opposite to the equal angles is always . - Hence, proved.
5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠ B = ∠ C.