Some More Criteria for Congruence of Triangles
We have already mentioned how checking for just congruency in the three angles isn't enough to guarantee congruency between two triangles.However, this isn't the case when dealing with sides. As it turns out, equality of all three sides of one triangle to corresponding three sides of another triangle are enough for congruence between the two triangles.
Theorem (SSS congruence rule) : If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
Now, let's talk about right-angled-triangles. In this case we observe that two right triangles are congruent if one pair of sides and the hypotenuse are equal.
Remember: The right angle in this case, is not the included angle.
Theorem (RHS congruence rule) : If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.
Note: The short hand
Example 7: AB is a line-segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B. Show that the line PQ is the perpendicular bisector of AB.
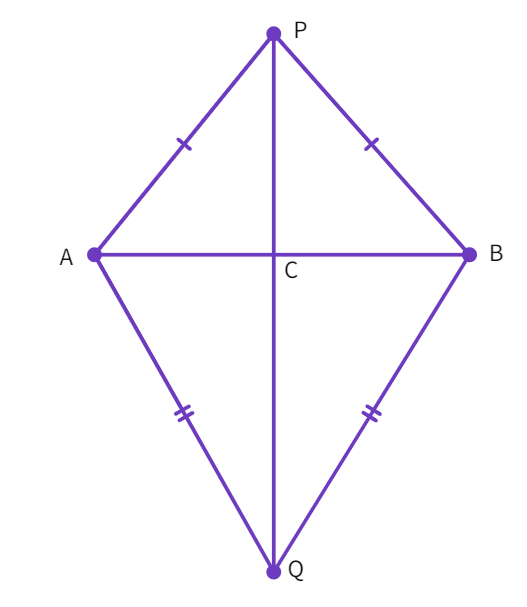
- Given: PA = PB and QA = QB.Let PQ intersect AB at the point C. Considering the triangles ∆ PAQ and ∆ PBQ:
= BP, AQ = and PQ = (Common) - By
congruency rule, we have: ∆ PAQ ≅ ∆ - By CPCT: ∠ APQ = ∠
- Now, considering the triangles ∆ PAC and ∆ PBC: AP =
, PC = (common) and ∠ APC = ∠ . - By
Congruency rule: ∆ PAC ≅ ∆ - By CPCT: AC =
(i) and ∠ ACP = ∠ - Since we have: ∠ ACP + ∠ BCP =
°, we get: ∠ ACP = ° which further gives us - ∠ ACP = ° (ii) - From (i) and (ii), we can conclude that: PQ is the perpendicular bisector of AB.
Example 8:P is a point equidistant from two lines l and m intersecting at point A. Show that the line AP bisects the angle between them.
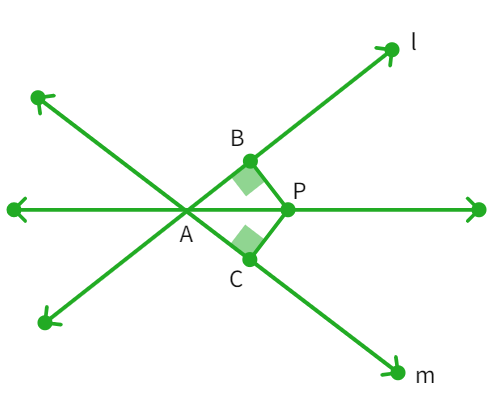
- Given: Lines l and m intersect each other at A with PB ⊥ l and PC ⊥ m. Also PB =
as point P is equidistant from l and m. - Considering the triangles ∆ PAB and ∆ PAC: PB =
, ∠ PBA = ∠ = ° and PA = PA (common) - By
rule we get: ∆ PAB ≅ ∆ - By CPCT: ∠ PAB = ∠
i.e. bisects ∠ - Hence, proved.
