Some Properties of a Triangle
Using the criteria we have studied in the previous section, we can talk about triangles having two sides equal and analyze their properties.
Say, we have a triangle in which two sides are equal, say each equal to 3.5 cm and the third side equal to 5 cm. Do you remember what is such a triangle called ?

A triangle in which two sides are equal is called an
A triangle in which two sides are equal is called an isosceles triangle. So, ∆ ABC, as shown below, is an isosceles triangle with AB = AC.
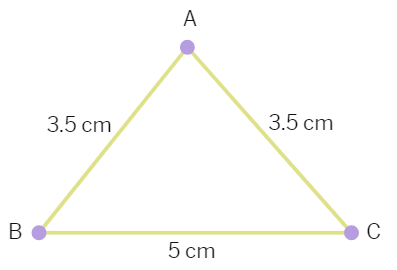
Now, measure ∠ B and ∠ C. What do you observe ?
Upon studying isosceles triangles, we notice that in each of such triangles, the angles opposite to the equal sides are always equal.
This is indeed true for any isosceles triangle and happens to be an extremely important geometric revelation. We can try to prove this result now.
Theorem : Angles opposite to equal sides of an isosceles triangle are equal.
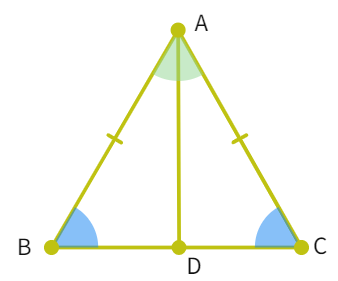
Given: we have an isosceles triangle ABC, where the side AB and AC are equal.
Construction: Drawing the angle bisector for ∠A and letting it coincide with the third side i.e. BC at point D, we get the figure shown above.
- Considering the triangles ∆ BAD and ∆ CAD: AB = AC (given), ∠ BAD = ∠
(by construction we have as an angle bisector) and AD = AD (Common) - So, by
congruency rule,∆ BAD ≅ ∆ - Thus, by CPCT: ∠ ABD = ∠
i.e. ∠ B = ∠ - Thus, the angles opposite to equal sides in a triangle are also equal.
Now, let's check if the converse also true i.e. if two angles of any triangle are equal, are the sides opposite to them also equal ?
Theorem : The sides opposite to equal angles of a triangle are equal.
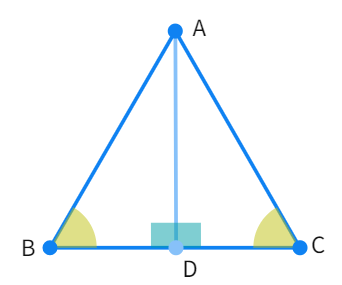
Let's draw an altitude from the vertex A that drops down and intersects the side BC at point D. Since, this is an altitude, the angle it makes at the intersection point D is a
- Considering the triangles ∆ADB and ∆ADC we get, ∠B = ∠C (given), AD = AD (common) and ∠ADB = ∠ADC = 90º
- By
congruence we get, ∆ADB ≅ ∆ - By CPCT:
= - Meaning that the sides opposite to equal angles in a triangle are also equal.
Example 4: In ∆ ABC, the bisector AD of ∠ A is perpendicular to side BC as shown below. Show that AB = AC and ∆ ABC is isosceles.
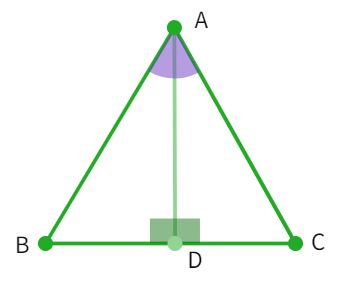
- Considering triangles ∆ABD and ∆ACD: ∠ BAD = ∠ CAD (given as
is bisector), AD = AD (common) and ∠ ADB = ∠ ADC = ° (given) - Thus, ∆ ABD ≅ ∆
using the congruency rule - By CPCT: AB =
i.e. ∆ ABC is an isosceles triangle - Hence, proved.
Example 5 : E and F are respectively the mid-points of equal sides AB and AC of ∆ ABC. Show that BF = CE.
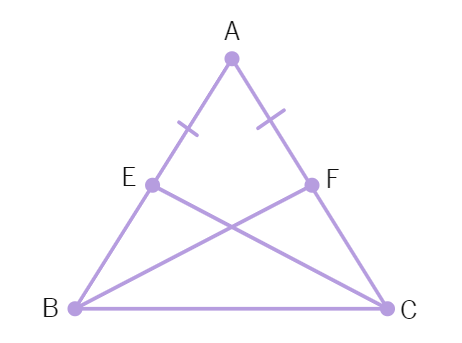
Solution: Considering the triangles ∆ ABF and ∆ ACE:
(i) AB =
(ii) ∠ A = ∠
(iii) AF =
Thus, ∆ ABF ≅ ∆
Therefore, BF =
Example 6: In an isosceles triangle ABC with AB = AC, we have points D and E on side BC such that BE = CD. Show that AD = AE.
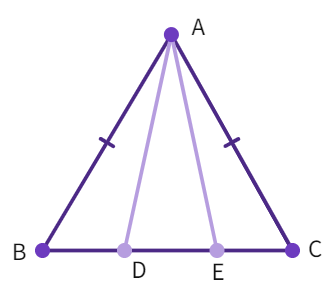
- Considering the triangles ∆ ABD and ∆ ACE, AB = AC (given) (1), ∠ B = ∠ C (
opposite to sides) (2) - Also we have been given that, BE = CD. So, BE – DE = CD – DE i.e.
= (3) - By
congruency rule: ∆ ABD ≅ ∆ - By CPCT: AD =
- Hence, proved.
